人工智能(AI)大模型的客观评测,有助于推动大模型行业的健康发展。然而,当前业内的基准测试(benchmark)层出不穷,充斥着各种评测乱象。
更值得深思的是,当一个模型在某个基准测试上的表现优于另一个模型时,这究竟是反映了模型间的真实的差异,还是仅仅因为选择了特定的问题而“运气好”?
从根本上说,评测就是实验,但有关评测的研究在很大程度上忽视了其他科学中有关实验分析和规划的研究,业内缺乏对这一问题的深入研究。
今日凌晨,OpenAI最强竞对、知名大模型初创公司Anthropic在其最新博客中试图回答这一问题。他们通过借鉴统计理论和其他科学中实验分析和规划的研究,向人工智能行业提出了一些建议,以便以科学的方式报告语言模型评测结果,最大限度地减少统计噪声,增加真实信息量。
相关研究论文也于前几日以“AddingErrorBarstoEvals:AStatisticalApproachtoLanguageModelEvaluations”为题发表在了预印本网站arXiv上。

论文链接:https://arxiv.org/abs/2411.00640
建议1:使用中心极限定理
评测通常由数百或数千个不相关的问题组成。例如,MMLU(测量大规模多任务语言理解能力)会包含各种各样的问题,比如:
谁发现了第一个病毒?
=4−5的倒数是多少?
“法理学是法律的眼睛”是谁说的?
要计算总体评测分数,需要对每个问题单独评分,然后总体分数(通常)是这些问题分数的简单平均值。
通常,研究人员将注意力集中在这个观察到的平均值上。但Anthropic认为,真正感兴趣的对象不应该是“观察到”的平均值,而是所有可能问题的“理论”平均值。
因此,如果将评测问题想象成是从一个看不见的“问题世界”中抽取的,那么就可以了解该世界的平均分数——也就是说,可以使用统计理论来衡量潜在的“技能”,而不受“全凭运气”的影响。
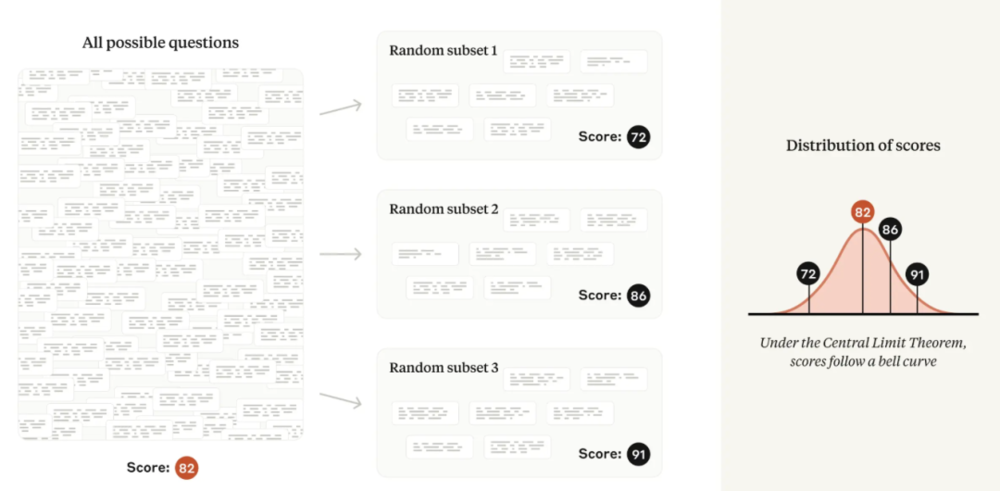
图|若想象评测问题来自“问题世界”,那么评估分数将趋向于遵循正态分布,以所有可能问题的平均分数为中心。
这种公式带来了分析鲁棒性:如果要创建一个新的评测,其问题具有与原始评测相同的难度分布,那么通常应该期望原来的结论能够成立。
用技术术语来说:在中心极限定理的相对温和条件下,从同一基础分布中抽取的几个随机样本的平均值将趋向于遵循正态分布。该正态分布的标准差(或宽度)通常称为平均值的标准误差,或SEM。
在论文中,他们鼓励研究人员报告从中心极限定理得出的SEM,以及每个计算出的评估分数——他们向研究人员展示如何使用SEM量化两个模型之间的理论平均值差异。通过在平均分数上加减1.96×SEM,可以从SEM计算出95%的置信区间。
建议2:聚类标准误差
许多评测违反了上述独立选择问题的假设,而是由一组密切相关的问题组成。例如,阅读理解评测中的几个问题可能会询问同一段文字。遵循这种模式的主流评测包括DROP、QuAC、RACE和SQuAD。
对于这些评测,每个问题从“问题范围”中选择的内容不再是独立的。因为包含关于同一段文本的几个问题所产生的信息量要比选择相同数量关于不同段落文本的问题所产生的信息量少,所以将中心极限定理简单应用于非独立问题的情况会导致低估标准误差,并可能误导分析师从数据中得出错误的结论。
幸运的是,聚类标准误差问题在社会科学中得到了广泛的研究。当问题的纳入不独立时,研究建议以随机化单位(例如,文本段落)对标准误差进行聚类,并在论文中提供了适用的公式。
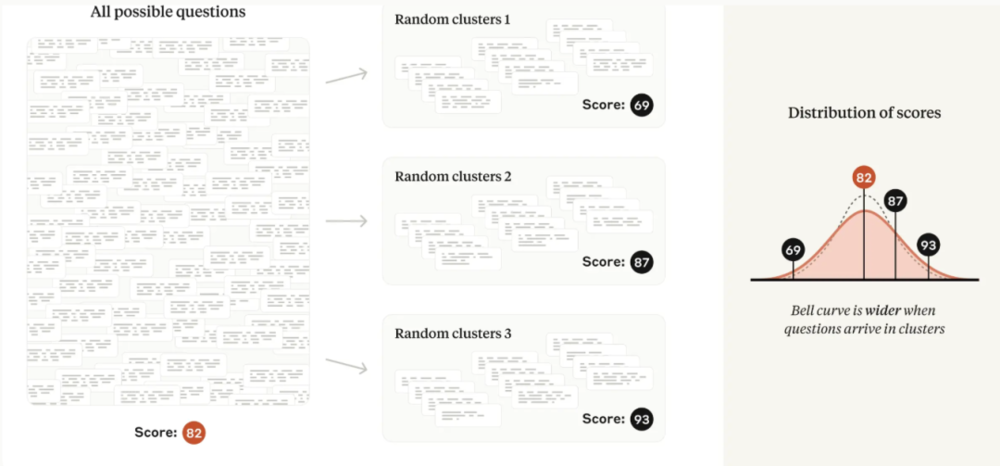
图|如果问题出现在相关的集群中(阅读理解评测中的常见模式),那么与非集群情况相比,评估分数将更加分散。
研究发现,在实践中流行评测的聚类标准误差可能是简单标准误差的三倍以上。忽略问题聚类可能会导致研究人员无意中发现模型能力的差异,而实际上并不存在差异。
建议3:减少问题内的差异
方差是衡量随机变量分散程度的指标。评测分数的方差是上文讨论的平均值标准误差的平方;该量取决于每个评测问题的分数方差量。
研究中一个关键见解是将模型在特定问题上的得分分解为两个相加的项:
平均分数(如果无数次询问相同的问题,模型将获得的平均分数-即使模型每次可能会给出不同的答案);
随机成分(实际问题分数与该问题的平均分数之间的差异)。
根据总方差定律,减少随机分量的方差会直接导致整体平均值的标准误差更小,从而提高统计精度。研究重点介绍了两种减少随机分量方差的策略,具体取决于是否要求模型在回答之前逐步思考(即CoT或思维链推理的提示技术)。
如果评测使用思维链推理,他们建议多次从同一模型中重新采样答案,并使用问题级平均值作为输入到中心极限定理的问题分数。他们注意到,Inspect框架通过其epochs参数以这种方式正确计算标准误差。
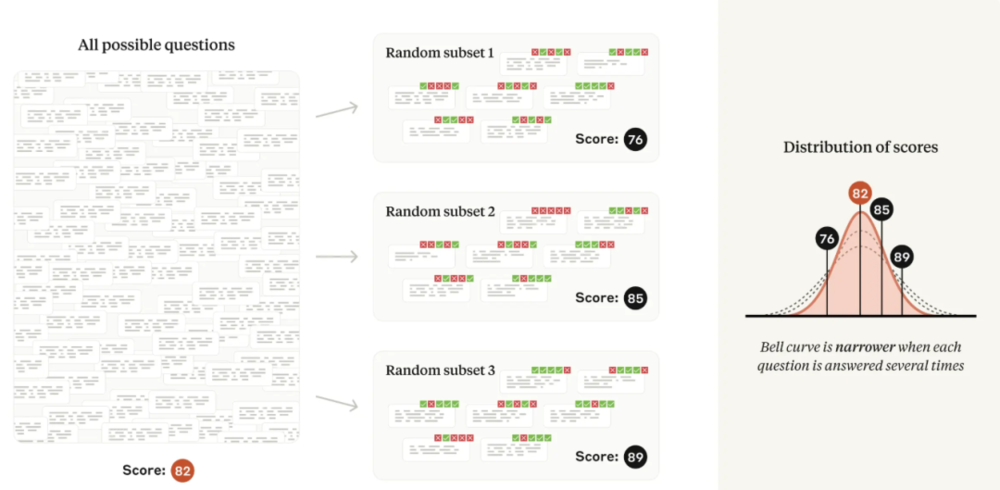
图|如果模型产生的答案具有不确定性,那么每个问题生成(和评分)多个答案将导致评测分数分散。
如果评测不使用思维链推理(即其答案不是“路径依赖”),那么分数中的随机成分通常可以使用语言模型中的next-token概率完全消除。例如,如果多项选择题的正确答案是“B”,那么只需使用模型生成token“B”的概率作为问题分数。研究团队表示不知道目前有哪个开源评测框架实现了这种技术。
建议4:分析配对差异
评测分数本身没有任何意义;它们只有在相互关联时才有意义(一个模型优于另一个模型,或与另一个模型能力相当,或超过某一个人)。
但是,两个模型之间测量到的差异可能是由于评测中问题的特定选择以及模型答案的随机性造成的吗?可以通过双样本t-test来找出答案,仅使用从两个评测分数计算出的平均值的标准误差。
然而,双样本检验忽略了评测数据中的隐藏结构。由于问题列表在模型之间共享,因此进行配对差异检验可以消除问题难度的差异,并专注于答案的差异。
研究中展示了配对差异检验的结果与两个模型的问题分数之间的皮尔逊相关系数之间的关系,相关系数越高,平均差异的标准误差就越小。
研究发现,在实践中,前沿模型之间主流评测中问题得分的相关性相当高——在-1到+1的范围内介于0.3和0.7之间。换句话说,前沿模型总体上倾向于对同样的问题做出正确和错误的回答。
由此可知,配对差异分析代表了一种非常适合AI模型评测的“自由”方差减少技术。因此,为了从数据中提取最清晰的信号,研究建议在比较两个或多个模型时报告配对信息——平均差、标准误差、置信区间和相关性。
建议5:使用效力分析
统计显著性的另一面是统计效力,即统计检验检测出两个模型之间差异的能力(假设存在这种差异)。如果评测中没有太多问题,则与任何统计检验相关的置信区间都会很宽。这意味着模型需要具有很大的潜在能力差异才能记录具有统计显著性的结果,而微小的差异很可能不会被发现。
效力分析是指观察计数、统计功效、假阳率和感兴趣的效应大小之间的数学关系。
研究展示了如何将效力分析的概念应用于评测。具体来说,他们向研究人员展示了如何制定假设(例如模型A的表现比模型B高出3个百分点)并计算评测应包含的问题数量,以便根据零假设检验该假设(例如模型A和模型B是平局)。
他们相信效力分析在很多情况下都会对研究人员有所帮助。他们的效力公式将告知模型评估人员重新抽样问题答案的次数(参见上面的建议3),以及在保留所需效力特性的同时可包含在随机子样本中的问题数量。
研究人员可能会使用效力公式得出结论,在特定模型对上运行具有有限数量可用问题的评测是不值得的。新评测的开发人员可能希望使用该公式来帮助决定要包含多少问题。
结论
统计学是在噪声环境下进行测量的科学。评测提出了许多实际挑战,而真正的评测科学仍未得到充分发展。统计学只能构成评测科学的一个方面,但却是至关重要的一个方面,因为经验科学的好坏取决于其测量工具。
Anthropic希望,论文中提出的建议将帮助人工智能研究人员比以前更精确、更清晰地计算、解释和传达评测数字,并且鼓励他们探索实验设计中的其他技术,以便能够更准确地理解他们想要测量的所有内容。
