不少同学在初学线性代数时感到迷茫、痛苦,体会不到课程的实际意义。这很大程度上是因为,教材为了由浅入深、循序渐进,须从基础的抽象概念讲起,而真正直观的部分,往往要等到后面的细分领域或具体应用。于是初学者往往知其然,不知其所以然;只见树木,不见森林。希望本文能让你换个视角,以轻松有趣的日常眼光,看到一个不一样的线性代数。
本文是系列文章《N文粗通线性代数》的第三篇。我们在上篇文章中通过矩阵初等变换来引入矩阵的逆及其性质,讨论了线性方程组的求解过程。线性方程组解的结果只有三种可能:无解,有唯一解,有无穷多个解。那么,这其中又有什么规律呢?
往期文章:
第一篇:矩阵乘法
第二篇:逆矩阵
撰文|吴进远
上回书说到,某近视宅男,某日下楼到早点铺买早餐。眼镜忘在家里,看不清黑板上写的价目。于是,宅男就一边排队,一边听着前边顾客买早点的品种数量,和服务员小妹报的总价,据此计算各种早点品种的单价。
一通采集数据,分析计算之后,近视宅男求出了线性方程组系数矩阵的逆矩阵,算出了食品单价,买了早餐。一边吃,一边陷入了沉思。
(1)几笔买卖定乾坤?
我们知道,只有正方形的矩阵才可以求出逆矩阵。具体在我们这个买早餐的问题中,三个未知数,需要正好三笔交易,或者说三个线性方程,才可以求出未知的食品单价。但在现实世界中,我们完全可能遇到不是正好三笔买卖的情况,这些情况下,我们的计算会遇到什么问题呢?
从直觉上我们知道,方程个数少于未知数的个数,肯定无法求出唯一解。可是,假如二者相等,就一定能求出唯一解吗?更进一步,要是方程的个数比未知数的个数还多,情况又会怎么样?我们下面一步步地分析一下:
为了直观地讨论这些问题,我们把三种食品的单价画在一个三维的坐标系中。下面的这些图中:
水平方向是油饼单价x1,
竖直方向为茶叶蛋单价x2,
而豆腐脑的单价x3则指向纸面之外。
上面这个图中画出了一个平面(红色),它是线性方程组中的第一个方程的图像,也就是第一个顾客那笔买卖。
这位顾客买了一个油饼、一个茶叶蛋、一碗豆腐脑,总价14元。
仅仅根据第一笔买卖,我们显然无法算出三种食品的单价,但我们多少还是获得了一些信息。具体说,我们知道这三种食品的单价一定在这个平面的某一个点上。
比如这个平面和横轴相交在x1=14这个点上,这个点对应于油饼14元,茶叶蛋和豆腐脑免费。
尽管在现实中很少有老板这么定价,但这个点所对应的这一组单价与这一个方程是没有矛盾的。事实上,整个平面上所有的点都与这个方程没有矛盾,而真实的单价也处于这个平面上,就是我们图中标出的蓝色圆点。
的确,仅仅知道一笔交易,或者一个方程,我们没有足够的信息确定真实的单价。现在我们引入第二笔买卖,这个方程在图3中对应另一个平面(绿色)。
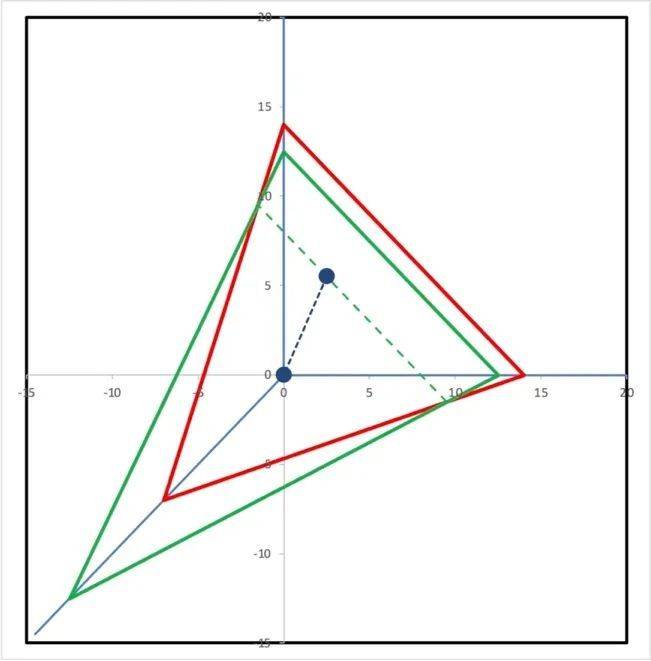
图3
这个平面与第一个平面在一条直线上相交。这就是说,同时满足两个方程的单价组合,只能处于这条直线上。尽管真实单价组合确实位于这条直线上,但我们仍然无法确认其准确位置。同时符合这两个方程的,仍然有无穷多个解。
显然,我们需要引入第三笔买卖。第三笔买卖对应的线性方程,在下面图中对应紫色的平面。
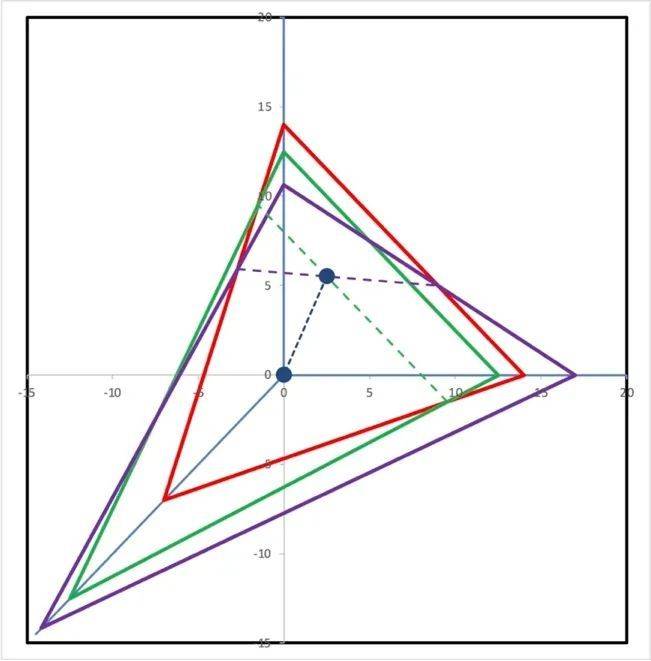
图4
这个新的平面与前面两个平面相交在一个共同的空间点上,这就是这个问题中真实的单价组合。因此,如果有N个未知数,至少要有N个方程才能求出唯一解。
那么,是不是方程数等于未知数个数就一定能求出唯一解呢?不一定。假设在买早餐这个例子中,宅男没有听清楚顾客3的交易数据,只用顾客1、2、4的交易数据来求解,就无法得到唯一解。
为了读者理解方便,我们把几位顾客的购买数据重新列在下表:
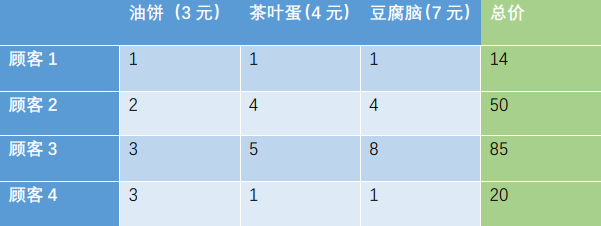
大家仔细观察,就会发现这位顾客4的交易数据是顾客1、2两组数据的线性组合:5×(顾客1数据)-(顾客2数据)。
因此,顾客4的数据没有提供任何新的信息,这一方程对应着图5中紫色的平面。而这个平面,与前面两个平面相交于同一条直线,这条直线上的所有点都同时满足三个方程。
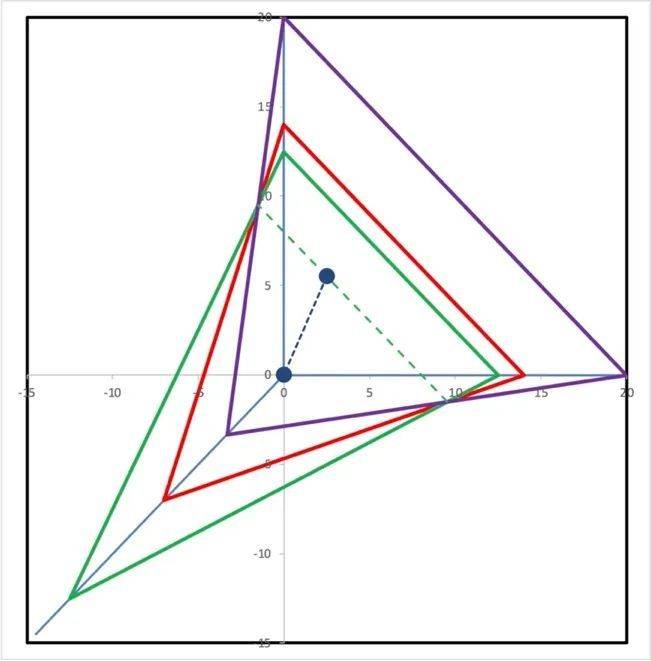
图5
不难想象,即使我们再增加若干方程,但如果新增加方程是原有方程的线性组合,则新增方程仍然不能提供新的信息,或者新的约束,所以仍然无法得到唯一解。这些方程画在上面的图中,是一组平面,而这些平面都相交于一条公共的直线。
(2)秩的那些事
线性方程组Ax=y解的性质,和矩阵A的秩(rank)关系密切。所谓秩,是指矩阵中线性独立的行或列的最大个数。前面买早餐的例子中,顾客1、2、3的三笔交易互相线性独立,因此这一个矩阵的秩rank(A)=3。而如果不包含顾客3,只考虑顾客1、2、4这三笔交易,则我们只能找到两个线性独立的行,第三行只是前两行的线性组合。因此,这样一个矩阵的秩rank(A)=2。
一个矩阵的列数m对应于方程组的未知数个数,而它的秩rank(A)则是线性独立的方程数的最大个数,也可以看成是能够提供独立信息的约束的个数。当rank(A)=m,我们管这种情况叫做列满秩,这时方程组如果有解,则其解是唯一的。
如果rank(A)
如果一个矩阵是“矮胖”的,或者说它的行数小于列数,显然它不可能是列满秩的。“矮胖”矩阵对应的方程组没有唯一解,如果有解也是无穷多个解。
当行数大于列数,矩阵变成“瘦高”的,对应的方程组才可能有唯一解(如果有解的话)。但在有解的前提下,具体什么情况还要看它是不是列满秩。
这两种情况通过前面的例子很容易理解。
(3)什么叫无解?
读者可能会问,为什么要强调方程组“如果有解”呢?难道还有方程组无解的情况吗?的确如此。
一个方程组里,每添加一个方程,就可能增加一个约束。这样,在理想的情况下,有效的约束够了,就可以帮助我们找到方程组的解。
继续增加方程,则可以帮助我们验算,检查前面算得对不对。
可是,在我们往方程组里添加方程时候,完全可能添乱,加进去自相矛盾的方程。这种情况下,这个方程组是没有解的。
比如买早餐的例子中,第一个顾客买了一个油饼、一个茶叶蛋、一碗豆腐脑,服务员小妹报价14元。假设另一个顾客买了两个油饼、两个茶叶蛋、两碗豆腐脑,这时报价应该是28元。假定顾客是位广东人,服务员小妹贴心地按照广东话来发音,于是我们的宅男就完全可能把“二十八”误听为“一三八”。这样一来,我们就遇到了一个自相矛盾的方程组。
在现实世界,数据采集传输中出现错误的情况非常普遍,因此方程组自相矛盾的情况也会非常普遍,而且自相矛盾的花样可能会非常复杂。为了搞清楚方程组有没有解,就需要用到另一个矩阵的秩:就是增广矩阵(A|y)的秩rank(A|y)。这里说的增广矩阵,就是把方程组Ax=y当中的y与A拼在一起。这里,y是纵向的一列数字,它可以看成是一个向量。而A当中各个列,也分别是同样维数的向量。
不难看出,如果方程组Ax=y有解,则y就一定是A当中各个列向量的线性组合。我们把y添加到A当中,新增加的这一列,与其他各个列是线性相关的。这样一来,增广矩阵(A|y)的秩rank(A|y)就不会比原矩阵A的秩rank(A)大。因此,方程组有解就等价于rank(A|y)=rank(A)。
反之,如果添了一列之后,秩增加了,即rank(A|y)=rank(A)+1,则方程组必然是自相矛盾的,没有解。
我们把前面谈到的这些情况列个表出来,就一目了然了。
这里需要指出,当矩阵A不是满秩的时候,如果方程有解就会有无穷多个解,但不同情况下的“无穷多个”是不一样的。具体说,就是解空间的维数等于m-rank(A)。
比如我们买早餐的例子中,m=3。当只有第一个顾客数据时,rank(A)=1,这时解空间是一个平面,解空间的维数等于(m-rank(A))=3-1=2。
在第二个顾客,乃至第四个顾客的数据加进来后,rank(A)=2,这时解空间的维数等于3-2=1,解空间是一条直线。
当第三个顾客的数据加进来后,rank(A)=3,这时解空间的维数等于3-3=0,于是解空间成为一个点,解的个数从无穷多变成了1,方程存在唯一解。
(4)零元购与齐次线性方程组
我们有时候会遇到齐次线性方程组,也就是Ax=0。“齐次”的意思说的是方程中只有未知数x的一次方项,没有常数项,或曰没有未知数x的0次方项,因此各个项中的方次是“齐”的。
由于方程组右边等于0,因而它的增广矩阵的秩显然不会增加。因此齐次线性方程组肯定是有解的,我们用肉眼就可以看出x=0显然是方程的解。
可是问题来了,除了x=0这样一个平凡解,齐次线性方程组Ax=0还会不会有不等于0的解呢?从前面讨论我们知道:rank(A)
为了便于理解,我们画出下面这个图,图中的每个平面相当于一个线性方程,这三个平面对应的方程是线性无关的。每个方程的右端常数项都等于0,其几何意义是每个平面都经过原点。
上面图中,三个平面只存在唯一一个公共交点,也就是原点。因此,当rank(A)=m的时候,方程组有唯一解,也就是说,只有x=0这样一个平凡解。
如果三个平面对应的方程存在线性相关(比如秩等于2),它们之间的空间关系就可能看起来像这样:
由于每个方程右边也都等于0,因此每个平面也都经过原点。不过由于三个方程是线性相关的,这三个平面有无穷多个公共点。
在秩等于2的情况下,这些公共点构成一条直线,这条直线也通过原点。这样,除了x=0这一个平凡解,这条直线上其他地方也是方程组的解,或者说,这个齐次线性方程组存在非0解。
在实数中,只有0乘以一个数其乘积才会是0。因此对于非零解,我们有时不容易想象。实际上,一堆不完全是0的数和另一堆不完全是0的数相乘,它们的乘积相加,确实可能得出一个0。这种情况并不难发生,比如只要两组数相乘之后,乘积有正有负,它们就完全可能相互抵消为0。再比如所有不等于0的数在矩阵相乘时都完美错过,都与0相乘,则结果也是0。
在线性代数中,所有元素都为0的矩阵叫零矩阵。零矩阵与任何矩阵相乘自然会得到零矩阵,但反过来却不一定。事实上,两个非零矩阵相乘,也完全有可能得到零矩阵。一个存在非零解的齐次线性方程组,实际上就是两个非零矩阵相乘得到零矩阵的例子。
齐次线性方程组在我们买早餐的例子中会是什么情形呢?首先,我们的宅男听到前面的所有交易的结果都是0,可以想象这种“零元购”是个非常欢乐的情况。过去学校或者单位的食堂,有的时候因为管理员经营有方,经常能到菜市场采购到便宜的食材,一年下来会结余很多,于是到年底就会有一天“吃结余”。显然,如果所有食品的单价都为0,就会出现吃结余或者零元购的结果。
但是反过来却不一定。比如,仅仅根据下面两个顾客的购买数据,我们并不能确认所有食品单价都是0:
第一个顾客买了一个油饼、一个茶叶蛋、一碗豆腐脑,0元;
第二个顾客买了两个油饼、四个茶叶蛋、四碗豆腐脑,0元。
因为除了所有食品都不要钱的情况,我们完全可能找到使这两个方程成立的非零解。比如设想:
油饼、茶叶蛋、豆腐脑的单价0元、X元、-X元,上面两个方程就可以成立。
这一组单价表示油饼不要钱,茶叶蛋一颗X元,而买一碗豆腐脑不但不收钱,还会倒送X元的礼品券。这种情况在做买卖上听着不很合理,但在理论中,却是齐次线性方程组理论上存在的非零解。
现在,如果把第三位顾客的数据加进去:
假定他买了一个油饼、三个茶叶蛋、三碗豆腐脑,0元;
我们仍然不能确认所有食品单价都是0。因为他的购买数量向量是前两位的线性组合(第二位购买数量向量-第一位购买数量向量)。
只有再来顾客,他的购买数量向量与前几位的线性无关,整个矩阵变成了列满秩的,我们才能得到新方程组的唯一解,即所有单价都为0。(未完待续)
