为了理解一个数学概念，例如群或流形，人们典型地要经历不同的阶段。很明显，从熟悉这个结构的几个代表性的例子开始，然后了解由老例子建立起新例子。特别重要的是要了解由这个结构的一个例子到另一个例子的同态，即“保持结构的函数”。

一旦了解了这些基本之点，还需要了解什么？一个一般理论要想有用，就必须就某些特定的例子告诉我们些什么。例如，拉格朗日定理被用来证明费马小定理。拉格朗日定理是关于群的一个一般事实∶若G是一个群，其大小为n，则其任意子群的大小必是n的一个因子。要想得到费马小定理，就需要把拉格朗日定理用于“G为非零整数关于mod p 的乘法所成的群”这个特例。我们得到的结论（a^p≡a mod p）远非显然的。

然而，如果关于群G我们想要知道一点对于一般群并不一定为真的什么事情，又该怎么办呢？就是说，现在我们想要判定，G是否具有一个某些群具有某些群则不具有的性质P。既然这个性质是不能从群的公理导出的，看来似乎应该放弃群的一般理论，而只来看特定的群G。然而，在很多情况下，还有一种介乎其间的可能性∶对于群G，去鉴识它是否具有一个"相当一般"的性质Q，再看能否从Q导出我们关心的性质P。

下面是这一类方法在不同背景下的一个例子。假设我们想要确定以下的多项式是否有一个实根∶

方法之一是去研究这个特定的多项式，试着找出它的一个实根来。例如，在花了一番力气以后，我们可能会发现p（x）可以因式分解为

第一个因子恒为正，但是用二次方程公式于第二个因子，我们发现，

另一个方法则要用一点一般理论∶注意到p（1）为负，而当x很大时，p（x）也很大，然后再用中间值定理（若一个连续函数有时为正，有时为负，则必在中间某点为零）就行了。

注意，在第二种方法里，仍然需要某些计算，找出x的一个值，使得p（x）为负但是它比第一个方法里的计算要简单得多。在第二种方法里，我们是去证明 p（x）仍然具有一个"相当一般"的性质，即在某处为负，然后再用中间值定理结束论证。

在整个数学里这样的情况很多，在这些情况里，证明某一个一般的性质是特别有用的。例如，已经知道一个正整数n是素数，或者知道某一个群G是阿贝尔群（即对G中任意两个元g，h均有gh=hg），或者知道某一个映复数为复数的函数是全纯函数，然后就能作为这些一般性质的推论，关于这个对象，知道更多的东西。

当这些性质已经确定是重要性质时，它们就会给出一大类数学问题，其形式如下∶给定一个数学结构，并选择一些它可能具有的有趣性质，这些性质有哪些组合会蕴含其他性质？并非所有这些问题都是有意义的，但其中有一些问题是非常自然的，而当人们试图去解决它们时，一开始又时常是极难解决的。这时常是一个信号∶碰上了一个数学家称为“深刻”的问题。下面就看一个这样的问题。

群G称为有限生成的，如果G有一个元素的有限集合

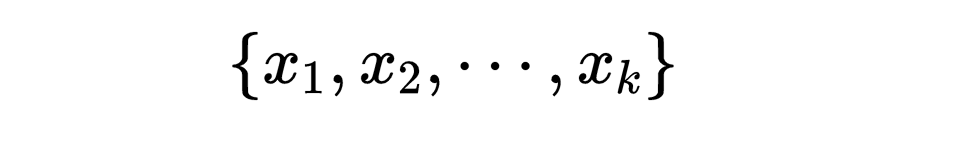
使得群的其余的元素都可以写成它们的乘积。例如

这个群就是一个有限生成的，证明它的所有元素都可以用4个矩阵通过矩阵乘积来生成，

第一步是证明

现在考虑第二个性质。若x是群G的一个元，则说x是有限阶的，如果存在x的一个幂，恰好等于恒等元。这个最小的幂就称为 x 的阶。例如，在非零整数 mod 7的乘法群中，恒等元就是1，元素 4的阶是3，因为

至于3，它的前6个幂是3，2，6，4，5，1，所以它的阶是6。有一些群有一个特殊的性质，即存在一个正整数n，使得对于群的一切元素x，x^n都是恒等元，或者用一个等价的说法，即所有元素的阶都是n的一个因子。对于这种群，我们能说些什么？

现在先看所有的元素都以2为阶的情况。用e表示恒等元，我们的假设就是，对于每一个元素 a，a^2=e。如果用逆元 a^-1 去乘上式双方，就得出 a = a^-1。反向也容易证明，所以这种群就是所有元都等于自己的逆元的群G。

现在令 a ，b 是 G 的两个元。对于任意群的任意两个元 a，b，总有恒等式

而对于特殊的群G，则还可以由此导出 ab=ba。就是说，G自动地是阿贝尔群。

我们已经看到一个一般性质∶G的每个元平方以后均得恒等元，蕴含了另一个一般性质∶G为阿贝尔群。现在再加上一个条件∶G为有限生成群，而令

为生成元的最小集合，就是说，群G的每一个元素都可以用最小集合中的元素 构造出来，而且这些元素一个也不能少。因为群G是阿贝尔群，而每一个元素又都等于自己的逆元，就可以重新排列这些x_i的次序，把这个元素化为标准形式，即各个x_i只出现一次，而且依下标的次序排列。例如看下面的乘积

因为群G 是阿贝尔群，这个乘积就等于

又因为每个元都等于自己的逆元，所以这个元就等于

这就是标准形式。

这就证明了群G最多只有2^k个元素，这是因为对于每一个x_i都有两种选择，即或者包含或者不包含在标准形式中。特别是“群G为有限生成的”以及“群G的每一个非恒等元均等于自己的逆元”，这两个性质就蕴含了第三个性质∶群G为有限群。还可以很容易地证明，若两个元素的标准形式不同，则它们本身自然也不同，所以，群G确实恰好有2^k个元素（这里k是最小生成元组的大小）。

现在我们要问，如果使得对于一切元x都会有x^n=e的这个幂指数n>2，会发生什么？就是说，如果群G是有限生成的，而且对一切元x都有x^n=e，群G是否必为有限群？这是一个难得多的问题，最早是由本塞德提出的。本塞德本人证明了若n=3，则群G必为有限群，但是直到1968年前一直没有大的进展，1968年Adian和Novikov得到了一个值得注意的结果，即若n≥4381，群G不一定是有限的。当然，在3和4381之间还有很大的间隙，在这个间隙上建一座桥的工作进展很缓慢。只是到了1992年，才由Ivanov 改进到n≥13。想要体会一下本塞德问题有多难，只需看一下以下的情况就明白了∶甚至两生成元的群，若每个元的五次幂均为恒等元，此群是否有限都还未知。