文|史说百家

编辑|史说百家

使用大约330000颗矮星的完整样本，由盖亚DR3测量，仅限于银河南北立体角||%3C75∘在2 kpc的垂直距离内，我们根据投影的切向速度分析了银河系恒星盘的垂直结构。

从由其相应总体支配的选定子样本中，我们获得薄和厚圆盘尺度高度如下ℎ=279.7612.49pc和=797.2312.34分别是pc。

通过对整个样本的两个总体的和的同时拟合，假设这些尺度高度，我们估计银道面上厚盘与薄盘的数量密度比为/=0.7500.049，在银道面上有大量的厚盘星，可能与薄盘星一样多，这也表明存在比通常认为的更多的厚盘星。

那么薄盘之外存在更多的恒星吗？这是双盘模型可以解释的吗？

银河系(MW)由一些在观测上容易区分的成分组成，这些成分在空间分布、运动学和化学丰度上有所不同。

凸起、圆盘和晕这些结构与许多其他盘状星系相同，尽管在其中许多星系中，我们已经观察到薄盘和厚盘的存在。仅仅40年前，吉尔摩和里德发现了中波厚的圆盘一如今，这部分星系被认为是理解星系形成过程的重要组成部分。

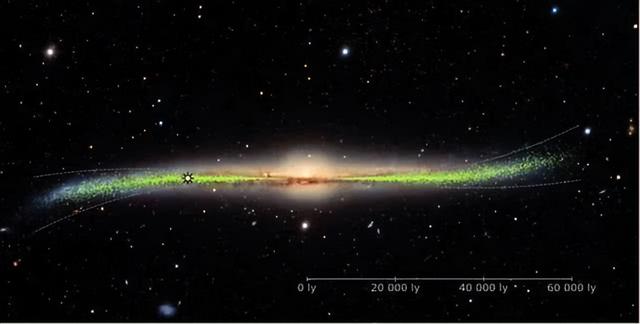
许多研究致力于测量薄盘和厚盘的标度高度，薄盘的结果大约从120到300 pc变化，而厚盘的结果范围从500到1900 pc。

最近Everall等人使用GAIA EDR3数据，估算了银河系盘面的垂直空间结构，以及垂直于银河系盘面方向上的银河系晕。考虑到样本的不完全性，Everall等人使用了一种基于泊松似然函数的方法。

他们发现银河系中垂直于银盘的密度分布，可以表示为两个指数剖面的总和，垂直尺度高度为260±3(stat)26(sys)PC的薄盘和尺度高度为693±7(stat)121(sys)PC的厚盘，以及恒星晕中的幂律密度分布。

研究仅限于垂直于银河系盘面的密度分布，在距银河系中平面2 kpc范围内，使用了一个完整的主序星样本，表观G星等在4到8之间。

尽管人们为理解它的物理性质付出了巨大的努力，但对于它的确切起源还没有一致的看法，人们一致认为厚盘是先前存在的薄盘动态加热的结果，薄盘是由(I)巨大分子云散射薄盘星、螺旋形或条状结构、小伴星系的轻微合并、恒星的径向迁移。

有人建议厚盘是由来自吸积破裂的卫星星系的恒星形成的，另一方面，其他人喜欢主张一个连续的垂直圆盘结构，由一系列单独的恒星单丰度群体连接，随着年龄的增长，这些群体由薄到厚，其综合垂直空间密度显示为两个圆盘。

要弄清楚哪一个被提出的形成场景发生在微波辐射中，唯一的方法就是详细研究银河系厚盘的特性。为了选择厚盘星，人们提出了几个标准:α元素的相对丰度、恒星年龄，或者仅仅是在银河中面以外1-2 KPC处的绝对垂直距离的一个切割。

尽管薄圆盘的高度远低于这个切割值，但仅位置不足以解开两个群体，需要不同的运动学和丰度切割来实现。

在这种情况下，可以测量标度高度，但不能计算所研究体积内的数密度比，这是理解厚盘性质的基本量。

我们的目标是选择盖亚DR3星的一个子集，在银道面上方和下方的两个立体角上对银河系进行全面采样，直到3 kpc的距离，对于这种情况，投影的切向速度可以用作星系的安全代理-恒星的速度。

这种方法过去曾被用来研究银河系的垂直结构和更高高度的动力学，只有天体测量数据。如今盖亚数据显著增加了天体测量和径向速度的恒星数量，但后者仍然只测量了一部分恒星(G ≲ 13)。

无论如何，Gaia允许我们将这种方法扩展到比过去的研究更远的地方，这意味着我们可以在采样的体积中获得更多厚的盘状恒星。

从选择的恒星中，我们可以对703，176颗恒星进行校正，其中87%有5参数解，13%有6参数解。只有视差和自行，我们计算近似（,)速度(U朝向银河中心V在银河旋转的方向)通过假设视线速度为零。

这是可以安全地完成的，因为在所选的银河帽样本中，它的投影贡献U和V速度很小，低于估计的速度误差。

为了支持我们的假设，我们比较了我们的近似与完整（,)盖亚DR3测量径向速度的子样本上的速度(只有数据的23%)，我们确认它们的差异足够小。从现在开始，所有的速度都是指近似速度或基于近似速度的速度。

（,)相对于LSR的速度(参见图1)，显示了少量但不可忽略的晕星，落后于LSR的旋转，通过拒绝那些2+2−−−−−−−√≥180公里秒−1。

经过这一切割，样本减少到684740颗。我们还发现了两个在极冠中很容易看到的疏散星团，即北部的Coma星团和南部的Blanco 1星团，但它们的存在并没有干扰我们的结果，因为它们的恒星数量与整体样本相比可以忽略不计。

图一。 （,)从盖亚提取的样本的速度。

从（,)速度，我们计算以半乳糖为中心的圆柱速度(远离银河中心)和(相对于银河自转)速度，假设相对于当地静止标准(LSR)的太阳运动、LSR的半乳糖中心切向运动和太阳半乳糖中心距离的下列值:（,,)⊙=（11.10,12.24,7.25)公里秒−1，,=−244.5公里秒−1和⊙=8科索沃保护团。

图二。圆盘样本的色阶图，通过消光和变红进行校正。盘状恒星显示为灰色，而盘状矮星显示为黑色。

盖亚DR3完整性，基于EDR3的已知信息，估计在星等19到21之间。

假设一个经常被引用的完备性值低至20.7，那么所有矮星被观察到3.4 kpc的距离，包括我们的两个圆锥体积。

但是完整性可能会受到损害，因为我们应用了质量削减。因此，我们进一步检查我们的盘矮星样本的完整性，以恒星的太阳为中心的圆柱半径平方的累积分布是沿着Z在扁平圆柱体体积上或硬币，其半径随着Z随着锥体的形状远离平面生长。

但每个点的分布应该是统一的。对每一处的不完整性进行估计硬币，如所示图3。

图3。339，876个盘矮星样本的完整性评价。

灰色线在图3是样本中恒星垂直位置的直方图，每100测量一次，显示了双锥体积采样的预期两个最大值分布，但请注意计数的不对称性，这在过去已被其他作者检测到。

从取样的体积形状来看，距离银道面100 pc以内的恒星非常少：两个顶点在=0。

越靠近银道面的恒星数量越少，采样的体积越小，这使得密度计算非常不稳定，容易出错，这就是为什么我们避开银道面进行密度计算。

最后，考虑到远离银道面垂直方向上超过2 kpc的完整性的巨大变化，我们将盘矮星的样本限制在垂直方向上的范围内2kpc来自银道面，因此我们的最终样本有337859颗恒星。

在我们的盘矮星样本中，我们检查了Z对于由间隔定义的不同子样本20公里长−1宽度。我们看到子样本的垂直分布，根据它们围绕MW的平均旋转速度而变化。

图4。不同高度垂直分布的KDE图间隔。

每条曲线对应一个20公里的箱子−1宽度，以南纬290至50公里为中心−1。灰色粗线是由薄圆盘支配的子样本，黑色粗线由厚圆盘支配。

细黑线是两者的混合，细虚线是旋转最快的样品，表现出显著的不对称性。填充的浅灰色和深灰色图对应于图例中定义的子样本：薄(−280%3C%3C−200公里秒−1)和厚盘(%3E−140公里秒−1)主导样本。

我们看到随着子样本从较快(薄盘)向较慢旋转(厚盘)转变，预期的变宽。特别是，我们注意到−280%3C%3C−200公里秒−1共享一个相似的形状集中在银道面周围(薄圆盘)，而子样本在−140%3C%3C−60公里秒−1(厚盘)共享更宽的形状。

中间的子样本表现出具有混合特征的变化曲线。我们还注意到旋转最快的样品−300%3C%3C−280(虚线在图4)表现出明显的南北不对称性，这是我们选择不将其包括在薄圆盘样本中的原因。

通过考虑6228颗矮星1000%3E||%3C2000pc和%3E−140公里秒−1，我们使用Python包scipy.optimize.curve_fit来拟合以下形式的函数，对于高度为50 pc的截锥，每25 pc计算一次的数密度，介于=−2科索沃保护团和=+2科索沃保护团。

由此产生的密度(黑点)和拟合(灰色曲线)可以在中看到图5，拟合产量0=7.204×10−53.075×10−6个人计算机，−3和=797.2312.34个人电脑。

图5。厚盘样品(1000 %3C||%3C2000pc和%3E−140公里秒−1)垂直数密度拟合。

图6。薄磁盘样本(100%3C||%3C200pc和−280%3C%3C−200公里秒−1)垂直数密度拟合。

至于银道面上厚薄盘数密度比的计算，我们计算了双锥体积中圆盘样本的垂直数密度，考虑了所有矮星100%3C||%3C2000个人电脑和没有切入，总计336899颗恒星。

我们拟合一个函数的形式：

在高度为100 pc的截锥上，每50 pc计算一次数密度，介于=−2科索沃保护团和=+2不包括科索沃保护团||%3C100个人电脑。

结果，包括前面小节中的比例高度，在中列出表1可以在中看到图7。

图7。使用等式同时拟合薄和厚盘的盘样本垂直数密度(一).

我们注意到拟合度高于测量的密度||≳700 pc。我们做了几个测试来拟合方程一，在以下条件下:

假如ℎ和估计,和；

假如和估计ℎ,和；

估计所有参数ℎ,,和。

在所有这三种情况下，拟合的标度高度与我们之前获得的显著不同，并且它们的百分比误差显著更高，尽管它们的RMSD更小，最后一种情况得到最小的一个，并且最接近点拟合。

估计所有参数时，对于精简磁盘参数的百分比误差分别达到184%和663%ℎ和分别是。因此，当给定拟合所有参数的自由度时，算法很难找到稳定可靠的值，即参数误差方面的最佳性能。

代价是在更高的情况下，不能正确拟合数据，是在我们之前估计ℎ和作为固定值给出。我们相信我们对薄圆盘和厚圆盘高度的估计表1是可信的，因为尽管没有进一步的信息来改进数据选择，这些子样本仍由这些群体所主导。

至于厚与薄的垂直数密度的比率，我们注意到，对于发现的参数，比率sech2（/)sech2（/ℎ)是最大值，等于/在=0，降低到at的5%||700 pc，超过该值趋于零。

这意味着方程的拟合，主要由数据驱动||%3C700如果我们把分数提高到这一点以上，结果不会有太大的变化。

我们证明了这一点，通过限制数据||%3C700,1000和2000个人电脑，我们发现两者都和在相应的内改变3水平，增加和随着样本在垂直方向上远离银道面而减少。

奇怪的是，覆盖面越大||所有参数的百分比误差越小，但这可能仅仅意味着||范围意味着找到的参数更加“稳定”。

假设时ℎ和估计,和，我们得到了一个很差的估计数密度对于薄盘和明显更小的与先前报道的值相比，该值看起来更像薄和厚盘的普遍接受值之间的平均值。

我们的慢速和快速旋转样本可能无法分别正确测量厚盘和薄盘的垂直剖面，这是一种可能性，或者假设的两个群体拟合是不够的，需要不同的模型。

另一种选择是，观察到的不对称，在这项工作中没有考虑，是足够重要的，需要加以考虑。

它提醒我们注意，将薄圆盘和厚圆盘的总和(或多或少被普遍接受的银河系模型)与高质量的盖亚DR3数据进行拟合，无法解释||%3E700pc，其中精简磁盘的贡献可以忽略不计。

以前的工作通常分别处理任一圆盘，但是同时装配两个圆盘似乎是一个更困难的任务。我们认为，我们工作中使用的近似值，将体积限制为两个圆锥体，并忽略视线速度的影响，不会使所得结果产生偏差。

研究从银河系的垂直密度分布中得出的薄盘和厚盘是否真的是不同的组成部分，它们是在不同的时间通过不同的形成机制形成的。为此，使用了来自新视野模拟的18个大质量盘状星系和来自卡拉狄加模拟的一个盘状星系。

这些模拟具有高空间分辨率，这使它们成为研究星系详细结构的有力工具。将两分量拟合应用于r波段垂直剖面，发现两分量薄厚盘结构在数值模拟中得到了很好的表现。

在银河系中，在更高尺度高度的恒星比那些需要解释的薄圆盘中的恒星要多。考虑到大多数厚盘恒星位于银道面上，那么仅基于详细的化学丰度，并且完全独立于运动学选择，分离靠近太阳的薄盘和厚盘种群将提供更清晰的答案。

阅读此文后，烦请您关注+评论，方便剩下后续事件有新的进展能够让您迅速关注到

参考文献：

1、吉尔摩湾；昏暗恒星上的新光III。朝向南极的银河结构和银河厚盘。

2、k .库伊肯；银盘中的质量分布——II。太阳附近银盘表面质量密度的测定。

3、比利尔公司；卡拉阿里；Ak，s；Yaz，e；依赖银河经度的银河模型参数。

4、尤里奇，硕士；伊维兹奇。；布鲁克斯，a。勒普顿；施莱格尔特区；Finkbeiner博士；新泽西州帕德马纳班；邦德，n。塞萨尔湾；罗科西，C.MSDSS的银河系层析成像。恒星数密度分布。

END