傅里叶光学 Fourier optics

近代光学的重大进展之一,傅里叶变换光学的简称。又称信息光学,对光学信号(光学图像)进行傅里叶变换,在空域(图像本身所在的空间)和空间频域(经傅里叶变换后的频谱空间)同时研究光学信号的行为。方法是通过透镜等光学器件和衍射等光学效应来实现傅里叶变换,并经过空间滤波手续来处理光学信号。
傅里叶光学包括空间滤波和光学信息处理、光学成像系统的脉冲响应和传递函数、波前再现和全息术等研究领域。它在空间频谱的架构内分析光学信号,通过修改空间频谱处理光学信息,用被改变的空间频谱评价成像系统的品质,已在相衬显微镜、图像和特征识别、黑白图像的假彩色处理、光学传递函数和像质评价、全息术等领域都获得了重要的应用。
1.单色光傅里叶变换
一幅单色光图像总是由缓慢变化的背景、粗大的物体和急剧变化的边缘、局部细节构成。傅里叶光学中用空间频率来描述光强空间变化的快慢程度,把图像中缓慢变化的成分看作图像的“低频“,而把急剧变化的成分看作图像的''高频”。它的单位是“1/毫米”,即每毫米中光强变化的周期数。空间频率等于0表明图像中没有光强变化(如一张白纸)。
通常一幅图像中既有零频分量,又有非零频分量,后者包含各种空间频率的分量。零频分量在物理中代表平均光强,称图像的直流分量,非零频分量又称交流分量。数学上可用傅里叶变换提取图像中给定空间频率的成分含量:
为的傅里叶变换,式中和分别是和方向的空间频率,指数函数表示空间频率分别为和的平面波。图像中对应于空间频率和成分的含量即式中的,如果低频分量对应的傅里叶系数大,表明图像总体变化较缓慢;如果高频分量对应的傅里叶系数!¥#@大,表明图像总体变化较为剧烈。如果仅有某一空间频率的傅里叶系数不为零,则该图像就是余弦光栅。
上式的逆变换为:
此式的物理意义在于,任何二维单色光物体或图像都可分解为沿方向和沿方向、具有空间频率和的一系列平面波的叠加。其物理意义是把复杂的函数分解为一系列简单基元函数的线性组合,而空间频谱只是与各基元函数对应的权因子。基元函数可形象地看成是一些不同取向,不同空间周期的余弦光栅,该光栅在物体或图像内的或分含量由空间频谱确定。
2.用夫琅禾费衍射实现傅里叶变换
根据傅里叶光学的理论,一幅图像可分解为一系列空间频率不同的余弦光栅。余弦光栅的透射率可表为。当某一频率的余弦光栅被波长为的激光照射时,会出现三个透射光束,如图1所示。

图1 余弦光栅的衍射效应
居中的为直接透射光,又称零级项。一对衍射光对称分布在直接透射光两侧,与零级光的夹角满足条件(光栅方程)。当衍射角较小时,该条件近似表为。用波长为的单色光(如激光)照射尺度为的图像,相同空间频率的衍射光具有近似相同的方向。根据傅里叶光学的原理,其振幅为该空间频率的傅里叶谱项,不同方向的衍射光对应于不同的空间频率的谱项,因此称为角谱。角谱与傅里叶谱的实质相同。当衍射光传播的距离足够大时,不同空间频率的角谱近似在空间分离,因此远场衍射效应能实现傅里叶变换。
用波长为的单色光(如激光)照射尺度为的图像,它的复振幅分布为,在距离图像为处的屏上会出现图像的衍射像。当远场条件成立时称为夫琅禾费衍射。一幅图像的夫琅禾费衍射具有傅里叶变换的效应,衍射屏上的复振幅分布就是的傅里叶变换。
3.透镜的傅里叶变换性质和傅里叶处理器
如果用波长为的单色光(如激光)照射图像,该图像的复振幅函数为,并用透镜或透镜系统将同一方向的角谱会聚到透镜焦面上不同的位置,角谱就转换为焦平曲上的空间频谱。透镜后焦面的复振幅分布就是的傅里叶变换,空间频率与后焦面上一点的对应关系为,式中为透镜的焦距。这里略去了不重要的相位因子。后焦面又称为傅里叶谱面或滤波平面。
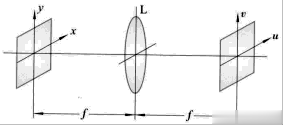
图2 透镜傅里叶处理器
图2是一个透镜傅里叶光学信息处理器,简称傅里叶处理器。原则上所有具备将同一方向的光束聚焦在空间一对应点的性能的器件都可能具备傅里叶变换的性能,如球面反光镜、自聚焦透镜等。
自从透镜对于相干光的复振幅信号的傅里叶变换效应被发现以后,光学图像的空间频谱就不再是抽象的数学概念,而变成了物理现实。透镜的傅里叶变换效应具有二维相干光并行处理、大容量的特点,价格非常低廉,但透镜的傅里叶变换效应只在接近光轴的所谓近轴区域内近似成立,而且是模拟变换。
4.系统和光学信息处理
两个傅里叶处理器可以串联起来,构成光学信息处理系统,如图3所示。

图3 4f系统
将输入图像放置在第一个傅里叶变换透镜的前焦面上,该平面就是系统的输入平面。用准直(平行)的相干光(如激光)照射,根据傅里叶光学的理论,在透镜的焦平面上将出现输入图像的空间频谱,该平面称系统的变换平面、谱平面或滤波平面,这一过程为输入图像的傅里叶变换。再用第二个傅里叶变换透镜对图像的空间频谱进行第二次傅里叶变换,即逆变换,便还原了输入图像。第二个透镜的前焦面与谱面重合,后焦面即输出平面。
一般情况下,取两个焦距均等于的透镜,系统长度为,称此系统为系统,为典型的光学信息处理系统。如忽略透镜的像差,输出图像与输入图像完全相同(-1倍倒像)。如果在谱面上设置空间滤波器,滤掉噪声或不需要的频谱成分,提取或加强感兴趣的信息的频谱,经傅里叶逆变换后,就得到经过处理的图像。
经典的光学仅在空域研究图像信号,而傅里叶光学重点讨论图像信号在傅里叶频域的行为。光学信息处理是在傅里叶光学的理论框架下建立的一门新的学科,研究如何对各种光学信息进行各类光学运算(加、减、乘、除、相关、卷积、微分、矩阵相乘、逻辑运算等)和光学信息的提取、编码、存储、增强、去模糊、光学图像和特征识别,以及各种光学变换(傅里叶变换、对数变换、梅林变换、拉普拉斯变换)等。
傅里叶光学把相干光处理系统看作是一个光学模拟计算机,它具有二维并行处理的能力、极高的运算速度(光速)及极大的容量等,这些都是目前数字计算机难以达到的。由于受到某些器件如实时空间光调制器性能的限制,运算速度远没有达到光学信息处理的理论极限,同时光学模拟处理的精度较低,灵活性较差,使它在应用上受到了一定的限制。
5.光电混合处理
早期的光学信息处理中,输入图像和滤波器用照相干板记录,经处理的输出图像也用照相干板记录,需经过显影、定影,全过程是非实时的。
近年来,开发出各种电寻址的空间光调制器,如液晶显示器(LCD)、磁光空间光调制器(MOSLM)等,当光波通过器件时,振幅(光强)或相位受到调制,复制了计算机内的输入图像函数和滤波器函数,再用电荷耦合器件(CCD器件)或数码相机记录输出图像。全部输入、滤波和输出过程由计算机控制,称为光电混合处理。
把光学信息处理的二维、高速、空间带宽积大等优势与电子计算机数字处理的灵活性和高精度相结合,是相对完善和有实用价值的系统。
6.图像和特征识别
图像和特征识别是光学信息处理的一个重要课题,称为相关识别。图4是一个光电混合实时相关识别的例子。

图4 光电混合实时相关识别
工厂中移动的产品零件在传送带上由200瓦卤钨灯照亮,由透镜1成像到像转换器一侧,激光束通过偏振分光棱镜照亮像转换器另一侧,使产品零件的像变为相干光图像,并由透镜2进行傅里叶变换,它的后焦面即谱面上放置匹配滤波器,并由透镜3进行傅里叶逆变换。当相同产品零件在传送带上出现时,透镜3的后焦面即输出面上就会出现相关亮点。如果出现的是不同的零件,相关亮点就不出现。
推荐书目
赵凯华,钟锡华. 光学. 北京:北京大学出版社,1984.
宋菲君,朱塔穆利亚 S. 近代光学信息处理. 北京:北京大学出版社,1998.
摘自:《中国大百科全书(第2版)》第7册,中国大百科全书出版社,2009年
