很多人以为在太空中看地球，是感觉旋转速度慢，但其实你根本就看不到地球自转。

不仅角速度太慢了，且和卫星发射形式有关。

为什么角速度太慢，就不容易察觉呢？

答案就在我们的眼睛上。

人的眼睛本身就是一个光学系统，就像一台摄像机，分辨率由我们的镜头（瞳孔）所决定。

我们看任何物体，本质上都是光线在我们的视网膜上“交织”而成。

而光的本质就是电磁波，穿过瞳孔的时候就会发生衍射。

很多人应该都有这样的经验，当用不同形状的小孔对着光源，把光斑照射在墙壁上，孔越小，光斑的形状也就越模糊。

如果点变得更小，就会形成明暗相间的光斑，这便是爱丽里斑。

这种衍射，在光学中称为夫琅禾费衍射

人在分辨足够小的物体时，本质上相当于分辨相邻的点光源。

两个过于靠近的点光源，会因为衍射图像互相重叠而不可分辨。

在光学中，把恰好能分辨的度数称为瑞利判据。

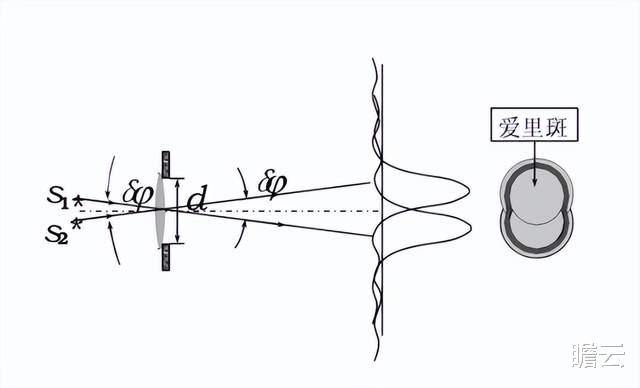
其公式为：

Δθ=1.22λ/D

θ为角分辨度，λ为光线的波长，D为孔径大小。

系数 1.22 通过爱里斑第一个暗圆环的位置计算得出。

这个数字更准确地说是 1.21966989……它是通过第一类贝塞尔函数一阶计算而来。

这个公式告诉我们，光波长越短，孔径越大，才有越高的分辨角。

瑞利判据公式适用于任何光学系统，当然包括我们的眼睛。

这和地球的自传角速度有什么关系呢？

因为瑞利判据本身，就决定了人眼的分辨率并不是一个固定的距离，而是一个角度。

正常人的瞳孔大小为2~4mm，肉眼最为敏感的可见光波长为555nm。

如果瞳孔大小取平均值，那么我们很容易得到人眼的角分辨度：

∆θ≈0.005°

相当于0.3角分，18角秒。

我们假设人与地表某点的相对速度为v，观察者距离地表的高度为h

那么在观察者眼中，单位时间转过的角度为：

a=360v/2πh

当 a≤∆θ时，我们无法察觉到地球的旋转；

当a＞∆θ，我们才能察觉到地球旋转。

显著大于时，我们才能看到明显的旋转，我们这里假设a＞5∆θ为显著大于。

一天86400s，地球角速度为360/86400，那么自转速度为466m/s。

求得，我们能看到地球旋转的最高高度为：

h=5340km

巧合的是，由于地球半径6371km，在这个高度看地球，地球差不多正好能充满我们的视野。

要能看到地球显著旋转，则 h=1068km。

很明显这个高度，我们只能看到地球的局部。

这也注定，当地球在我们视野中足够舒服的位置，是看不到地球自转的。

那我们近轨道看到的地球旋转画面，就是地球的自转吗？

其实根本就不是。

卫星主要有三种轨道：

低轨道：卫星飞行高度小于1000公里；中高轨道：卫星飞行高度在1000公里到20000公里之间；高轨道：卫星飞行高度大于20000公里。

理论上，在低轨道卫星上是可以看到地球显著旋转的。

速度较低的中轨道卫星，同样也能看到地球旋转。

然而由于卫星的发射方式，实际你根本看不到地球旋转。

我们知道太空中的照片都是卫星拍摄的。

而火箭发射，为了省力节约能源，是顺着地球自传方向发射的。

目前太阳同步轨道是逆行轨道，地球卫星是极少的

当卫星的速度超过地球的自转速度时，自然无法分辨地球的自传。

而卫星发射后距离地面轨道越近，速度越快。

我们知道第一宇宙速度是7.9km/s，这是航天器最小发射速度，也是最大运行速度。

这个速度远远高于地球自转，此时即便拍摄的地球旋转的照片，也是卫星公转产生的。

所以在近地轨道的卫星上无法拍摄出地球的自转。

随着卫星的不断升空，一直到达36000km的高空，卫星飞行的角速度才会逐渐减慢到与地球同步。这个时候，我们看到的地球是静止的，自然看不到地球的自转。

如果要看到地球的自转，那么卫星还需要往更高的高度飞行。

但其实为了实用的需要，人类的卫星最高轨道就是36000km。这就注定了人类无法亲眼观察地球的自转。

如果卫星的高度再升高， 卫星速度足够慢。

甚至我们到达月亮轨道，太阳同步轨道，还能看到地球旋转吗？

很遗憾根本看不到。

因为前面我们已经计算出，要看到地球的自转，高度必须要在5340km以下。

月地距离38万公里，如果我们要在月球上看到地球旋转。

易得，地球的旋转速度需要达到3.3km/s，而要显著看到地球旋转速度则超过10km/s，这已经大于第一宇宙速度，地表所有非结合物体都会飞出去。

总之，无论地球自转，我们眼睛的分辨率，还是卫星发射方式，甚至万有引力本身，都决定了我们根本无法亲眼看到地球的自转。

而这些的背后，都由物理法则所决定。