2000多年前，古希腊哲学家毕达哥拉斯预言，我们的世界建立在数学之上。然而，很多人当时将这个预言视为笑话。宇宙是一个实体，我们可以看到它、摸得着它，但数学却是一个抽象的概念。宇宙怎么可能是由数学构建而成的呢？

2022年1月24日，证明这个理论的论文出现了，中国科技大学的潘建伟教授和他的团队首次用实验证实：描述量子力学必须要使用复数。这一发现表明复数与实体世界之间存在着对应关系。为什么人类发明的数学可以帮助我们破解宇宙的秘密呢？这背后到底有什么更深层的原因？

让我们回到公元前6世纪，一群希腊人正在爱琴海上举行派对。聚会的高潮是杀害一位叫做希帕索斯的人，人们把他扔进大海，活活淹死了。而这些杀人凶手竟然都是必达格拉斯派的数学家，古希腊的高级知识分子。为什么数学家要杀人呢？这是因为他们要保守一个惊天的秘密。

秘密是这样的：首先，让我们画出一个正方形，假设这个正方形的边长为1。连接正方形的对角，我们得到了一条线，问这条线有多长？今天的初一学生都能立刻回答，这条线的边长是根号2。然而，古希腊人还不知道什么是根号，他们费尽心机，也计算不出这条边的准确数字。最接近的一个长度值是707/500，也就是说这条边接近1.414，但显然又不完全相等。

这个问题打破了古希腊人对世界的认识。他们认为世界与数应该是一一对应的关系，比如2只羊、5把弓，7个贝壳这都没问题。但是根号2代表什么呢？莫名其妙地出现了无理数，这打破了他们对世界的基础逻辑。比达格拉斯派吓坏了，这会不会说明世界是虚幻的呢？

为了保守这个秘密，他们只能杀死发现无理数的人，就是希帕索斯。这就是历史上非常有名的第一次数学危机。然而，数学这种东西有一个特性，一旦某个公理或公式被发现，很快就会被其他人发现。无理数并不难找，反而可以说是随处可见，当越来越多的无理数被发现时，整数的大厦就轰然倒塌了。除不尽意味着什么呢？似乎意味着我们的世界并不那么完美，它存在着不确定性。

事实上，我们的世界很有可能就是不确定的。科学家观测组成世界的微观结构，本身就是一种概率。咱们来观察一下微观世界。虽然从来没有人见过真正的原子结构，但下面这个图像已经非常震撼了。这是铂纳米粒子，铂就是我们通常说的是白金。这个球上的每个小点都是一个单独的铂原子，目前这个球状的区域里大概有27,000个铂原子。

原子看上去像个小球，但实际上它并不是小球。我们还能近距离地观测原子吗？科学家使用最先进的MRI，即核磁共振仪，拍摄了单个原子的图像。虽然图像不是很清楚，但大家需要非常仔细地观察。这就是一个原子自旋状态的变化，这才是原子的庐山真面目。

那么，我们还能更贴近原子吗？不可能了。现在的科技完全达不到这一点，只能用三维动画来模拟原子内部的样子。电子以超高的速度围绕着原子核运转，因为原子核太小，而电子的运动速度又太快。看上去电子既出现在这里，又出现在那里，所以形成了电子云。电子是无法精确描述的，通常使用概率波来表示。理论上，电子可以出现在任何地方，就好像电子能够穿墙一样，这种现象称为量子隧穿效应。这说明不确定性是量子世界的常态。

时间来到1425年，意大利著名建筑师布鲁内莱斯基画了一幅奇怪的画。以前从来没有人见过这样的画。画里的空间好像全部都指向了一个点，离这个点越近，离观察者就越远，受到的压缩程度就越大。如果这个点足够远，一切事物、人、建筑，甚至山脉和海洋，都可以压缩进这个零维的点。所以这个点不仅是零，也是无限的。在今天的绘画学上，这个点被称为灭点。

在布鲁内莱斯基画出灭点之前，所有的画都是平的，没有空间透视关系。例如，十字军东征图中，骑着马的十字军领袖和城堡差不多大，而城上的弓箭手又变成了小矮人，这些都是扁平失真的二维图像。

关于灭点，还有一个有趣的故事。德国主教尼古拉斯库萨与布鲁内莱斯基是同时代的人，他曾长时间观测夜空。最后，他得出了一个惊人的结论：地球不是宇宙的中心。大主教是怎么得出这个惊人的结论的呢，因为他没有在宇宙中看到任何灭点。布鲁内莱斯基的画使欧洲的数学家们意识到不能再回避零与无限了。

200年后，一位全世界初中生的敌人现身了，他就是法国人迪卡尔。笛卡尔有两件事特别有名，一是他的哲学思想，用一句话总结就是“我思故我在”。第二件事更了不起，就是笛卡尔发明了平面直角坐标系，让初中生痛苦无比的解析几何。据说笛卡尔曾经想过，x轴和y轴能不能从1开始呢？他马上就发现那是不可能的。0必须排在-1与1之间，没有0整个坐标系就不存在了。

1927年，比利时天体物理学教授勒梅特提出了一个极其震撼的理论：宇宙大爆炸。今天主流的物理学界是这样解释的：距今138亿年前，宇宙产生于一次大爆炸，宇宙是从无到有的。它最初就是零，早期宇宙经过一次猛烈的爆炸，然后宇宙常数趋向于0，空间开始正常膨胀。按照这个理论，宇宙似乎有一个开始，但是没有结局。

这样看,平面直角坐标系就是一个二维化的数学宇宙。它有起点0，同时向四周发散，形成了无限的空间。数学再一次表现了它的预言能力。

随后，科学家们在宇宙中发现了更多的0与无限。这就是人类拍摄的第一张黑洞影像。这是位于M87星系中心的超大质量黑洞。黑洞是一个非常神秘的地方，越趋近黑洞，时空曲率越大，因为黑洞的体积为零，所以曲率将会趋向于无穷。光也无法从黑洞中逃离出来。

据意大利科学家预测，宇宙中黑洞非常多，甚至银河系就有可能有1亿个黑洞。这些黑洞就是零和无限的结合点，数学与宇宙似乎有着剪不断的联系。无理数好像预言了世界的不确定性，0与无限似乎在讲述宇宙的开端与结束。但是这些还不是最神秘的，真正烧脑的部分才刚刚开始，那就是虚数的出现。

时间来到16世纪上半页，有个叫塔塔利亚的数学家，以一己之力独自解开了一元三次方程。在那个时代，这样的知识是无价之宝。塔塔利亚靠着数学比赛和解题能够挣到很多奖金，所以解方程的秘密是不会让任何人知道的。有一位米兰的医生，同时也是数学家卡尔达诺，千方百计地想要得到解题的方法。在他糖衣炮弹的攻势下，塔塔利亚就把解题方法告诉了他，但他要求卡尔达诺发誓永远不会把方法告诉任何人。

塔塔利亚是这样解题的，他将一个正方形扩展到三维，取一个三次方程：x^3 + 9x = 26。想象一个立方体边长为x，它加上一个9x的体积等于26。再将立方体的边长扩展y，得到一个新的边长为z的立方体，其中z等于x + y。将扩展出的体积分为7块，其中3块大的矩形棱柱的体积是x*x*y= xxy，还有3块小的矩形棱柱的体积是xyy。最后还剩一个小立方体，体积是y的三次方。

塔塔利亚将这6个矩形棱柱重新装配成一个大的立方体，其中一侧的长度为3y，另一侧为x + y也就是z，高度仍然是x。这个新的矩形棱柱的体积就是3yzx。卡尔达诺敏锐地意识到，这个体积等同于三次方程中的9x，所以3yz = 9。

将6个矩形棱柱装回去，还缺了一块，即最小的立方体。因此，在方程的两边各加上y的三次方，大立方体z的三次方就组装好了，它等于26 + y^3。

现在我们有两个方程和两个未知数。将z=3/y代入第一个方程，就得到y^6 + 26y^3 = 27。

现在看上去好像更复杂了，因为要解决六次方的问题了。但实际上，我们可以将y^3看成一个整体。

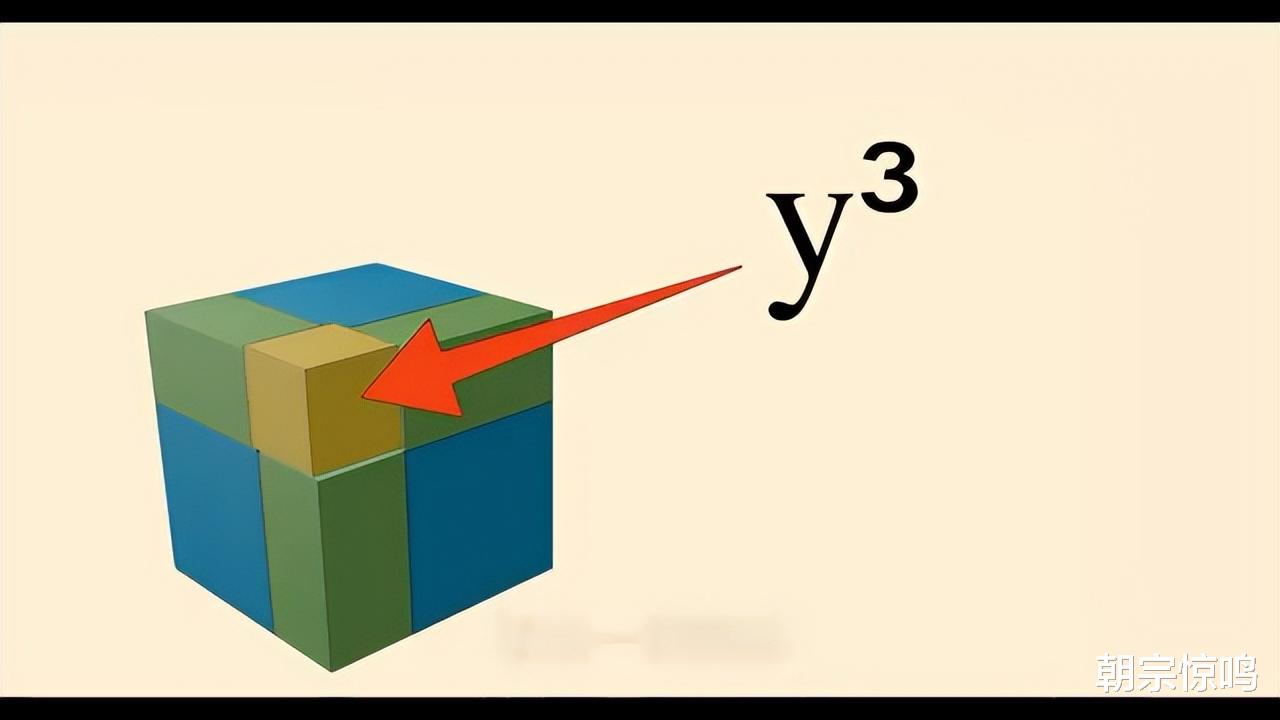
塔塔利亚再将这个三维图形变成二维，计算出小正方形的边长等于1。

由于z=3/y，所以z=3。从而得出x=2。这是一个极为了不起的思维过程，塔塔利亚得到了一个一元三次方程的正确解。虽然得到了塔塔利亚的解析式，但是塔塔利亚并没有给出证明。卡尔达诺用了好几年的时间，终于独立地推导出完整的证明步骤。接下来的事大家一定猜到了，他把一元三次方程的求解写成书出版了。虽然在书里，他明确提到这个方法是塔塔利亚发现的，但实际上还是违背了他的诺言。

卡尔达诺在解一元三次方程时，有时会得到一些奇怪的解，比如x^3 = 15x + 4。代入公式会得出一个从来没有见过的东西：根号-121。负数怎么能开方呢？卡尔达诺认为这种表达是没有意义的。他在书中说，这种现象似乎没有什么用处，但是这种奇怪的数就像是幽灵一样，总是存在于方程的解中。

前面我们提到的大数学家笛卡尔终于给这种数起了一个名字，叫做虚数。虚数表达为a + bi，其中a和b为实数，i等于根号-1。

1799年，德国数学家高斯假定实数与虚数和平面直角坐标系上的点一一对应。于是他就发明了震惊数学界的复平面。有人会说，这不和前面的平面直角坐标系一样吗？怎么就震惊数学界了呢？别看同样是横竖两条直线相交，复平面所赋予的思想内涵要深刻得多。可以说，人类对复平面的探索才走了一半的路，我们还远远没有参透复平面的真正含义。

下面我们使用最简单的概念来介绍一下复平面。举个初中数学的例子，假设给出一个方程：y = x^2 + 1。在平面直角坐标系中，就得到这样一个图形。

这个图形与x轴没有交集，所以没有根。根在哪里呢？其实不是没有根。如果把这个方程拓展到虚数的维度里，就得到了这样一个图形，图中标记的部分就是方程的虚数根，另一个根在纸的下半部分，我们看不见。

从这个最简单的一元二次方程可以看出，虚部的出现将我们引入到另一个维度。需要说明的是，这个维度并不是我们通常说的二维、三维，而是一个虚构的维度。在这个维度里，可以随心所欲，想要表现三维空间吗？那就是小菜一碟。

最直观的例子就是机场的控制塔。从雷达屏幕上，可以读出飞机的航线与实时的速度。在飞机降落时，有很多的变量，为了简化计算，就需要使用虚数i。虚数这么抽象的概念，为什么会有这么大的实际用途呢？

我们再回到复平面上。假设一架飞机的航向为3 + 4i。如果让飞机逆时针转动45度角，新航线是多少呢？

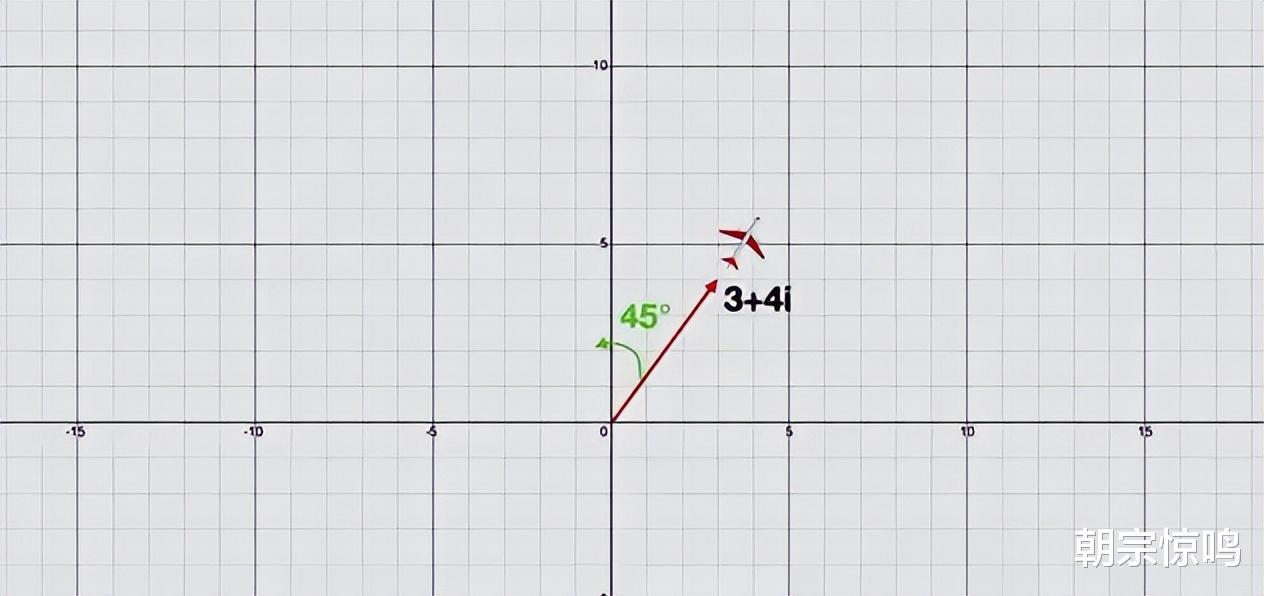
45度在复平面中表示为1 + i。只要把3 + 4i与1 + i相乘就可以了，最后得出-1 + 7i，这就是新的航向。

飞机除了在平面上转向，还会改变高度，这就又引入了新的维度，这些都需要使用虚数来计算。背后的原因是什么呢？这是因为每成一次i，实际上都是在复平面上旋转了90度。1乘i来到了i，0点，i乘i来到来到了0 -1点，再乘i来到了-i 0点，再乘i回到了0 1点。

我们一直乘i，按这个点就会在数轴上连续旋转起来。如果从x轴方向向下移动，就会得到一个螺旋，而这个螺旋在虚部上就是正弦波。

我们的世界很有可能是由波组成的，所以到处都是波。音乐、流体、量子力学中，波动力学都是波。从复平面上看，解释波动现象的最佳方法就是虚数。

我们再回忆一下虚数是怎么来的。它最先是解决三次方程中一个古怪的解，却可以用来描述大千世界。这真是太奇怪了。虚数到底是一个高度抽象的概念，还是像无理数0和无限一样真实地存在于我们的世界中呢？这一直是人们思考的问题。

现在我们回到文章开始介绍的中科大潘建伟教授的实验上。这是一个非常巧妙的实验。从两个粒子源各产生一对纠缠粒子，甲源产生A和B1，乙源产生B2和C。AC分别进入1号和3号探测器，B1和B2进入到2号探测器。强迫原本不纠缠的B1和B2进入到纠缠态，这个过程称为纠缠交换。最终，原本无关的a和c居然也产生了纠缠。潘建伟教授和团队用实验证实，这个过程用实数理论是无法描述的，必须使用虚数。这是一个非常重要的发现，虚数不虚，说明虚数在我们的世界里是真实存在的。

这就不禁让我们思考，数学到底是什么？为什么数学总是能带领人类去不断探索宇宙的本质？这个问题现在依然没人能够回答，所以也只能给出一种似是而非的答案。因为数与真实世界是一一对应的，如果宇宙有智慧，数学也许就是宇宙的思维规律。人类通过掌握数学，不断地探索宇宙的思维规律，进而揭开宇宙的真相。从这个角度上说，数学的本质是宇宙的逻辑。