为什么宇宙的最高温度是1.4亿亿亿亿摄氏度,最低温度却是零下273.15摄氏度。
我的第一层理解是,最高温度到零点的距离和最低温度到零点的距离之所以相差如此悬殊,是因为零摄氏度是以人类为中心线来定义出来的,开氏温标就不存在这个问题。
后面仔细想一想,这样的理解还是草率了。这个问题真正想传达的意思应该是,为什么人类生存的温度这么接近温度的下限,和绝对零度仅相差两个数量级,却极其远离温度的上限,和普朗克温度相差了32个数量级。
那我的第二层理解是,由于构成碳基生命的基础材料是有机物,维持有机物稳定状态的温度就决定了生命体居住的温度,而这一温度和绝对零度靠得就比较近。

在经典力学中,温度的本质是微观粒子运动剧烈程度的体现。现在我们假设有一群气体分子,并且保持这群气体分子的总压强不变。如果这群气体分子运动越剧烈,温度也就越高,所以气体所占据的空间体积就越大。如果气体运动剧烈程度降低,温度就降低,其气体所占的空间体积就缩小。
在压强不变的情况下,气体体积和温度呈线性关系,这种关系可以用二维坐标清晰地表达出来。x轴代表气体的温度,y轴则为气体的体积。而我们通过实验得出的数据就可以描点了。比如,当温度为零摄氏度时,气体的体积为一立方米;而当温度为50摄氏度时,体积为1.183立方米;当温度为100摄氏度时,体积为1.366立方米。现在三点连线形成一条直线,其关系是很容易得到的。
气体体积V=1/273.15 X T+1。当气体温度越低,体积就越小。做一个延长线相交x轴,通过关系式可以计算出这一点的坐标为-273.15。这就说明直到温度低至零下273.15摄氏度时,气体体积就为零了。

也就是说,在这一温度下,气体分子消失,不再运动。但是呢,在物理事实上,分子不可能不运动,所以体积不可能为零,温度也就不可能低至零下273.15摄氏度了。
那有人就会问了,能不能把这一空间中的所有分子原子移除掉,也没有任何光线射入到这一空间内,那是不是就意味着这一空间的温度可以达到绝对零度了呢?即便你拿掉空间中的所有物质,真空中也会不断随机产生正反粒子对,这就是量子涨落。
这些粒子从真空中诞生,也消灭于真空。量子涨落就会体现出温度,所以即便是没有任何物质的真空,也不可能达到绝对零度。
开头已经讲过了,温度的本质就是微观粒子运动剧烈程度的体现。粒子运动越剧烈,温度就越高。如果粒子运动剧烈程度有上限,那么温度就存在上限。前面一直说粒子运动剧烈程度,想要精确度量这种剧烈程度就需要用物理量量化。
在国际单位制中,只有七个基本量,分别是长度、质量、时间、电流、热力学温度、物质的量和发光强度。如果让你在这七个基本量选出几个来度量粒子运动的剧烈程度,你会选择哪几个呢?
你不妨先这样想,一个粒子的质量是固定不变的。如果在单位时间内,这个粒子运动经过的距离越长,那么速度就越快。运动就表现得越剧烈。所以描述粒子运动剧烈程度的基本量可以是质量、长度和时间。
长度和时间相除就是速度v,而质量m和速度v相乘就是动量。因此,动量就可以用来描述粒子运动的剧烈程度。一个粒子的动量越大,温度就越高。动量由质量和速度决定。如果引入狭义相对论,那么粒子的运动质量又由速度决定。所以粒子动量唯一的决定因素就是速度。
速度的极限我们都知道是光速。这个粒子是不可能达到光速的,所以运动剧烈程度就有了上限。严格来说,这个上限就是该粒子能够以黑体辐射形式辐射成波长为普朗克长度的电磁波。
那么它的温度就是普朗克温度。通俗一点说,这个粒子运动剧烈程度的上限值,必须要求这个粒子达到光速。可是这个粒子是不可能达到光速的,但是我们可以把它想象成能辐射波长为普朗克长度的光子。光子就是我们刚才说的以黑体辐射形式辐射的电磁波。所以这时候光子能量的最大值就是微观粒子运动剧烈程度的最大值,也就是温度的最高值。
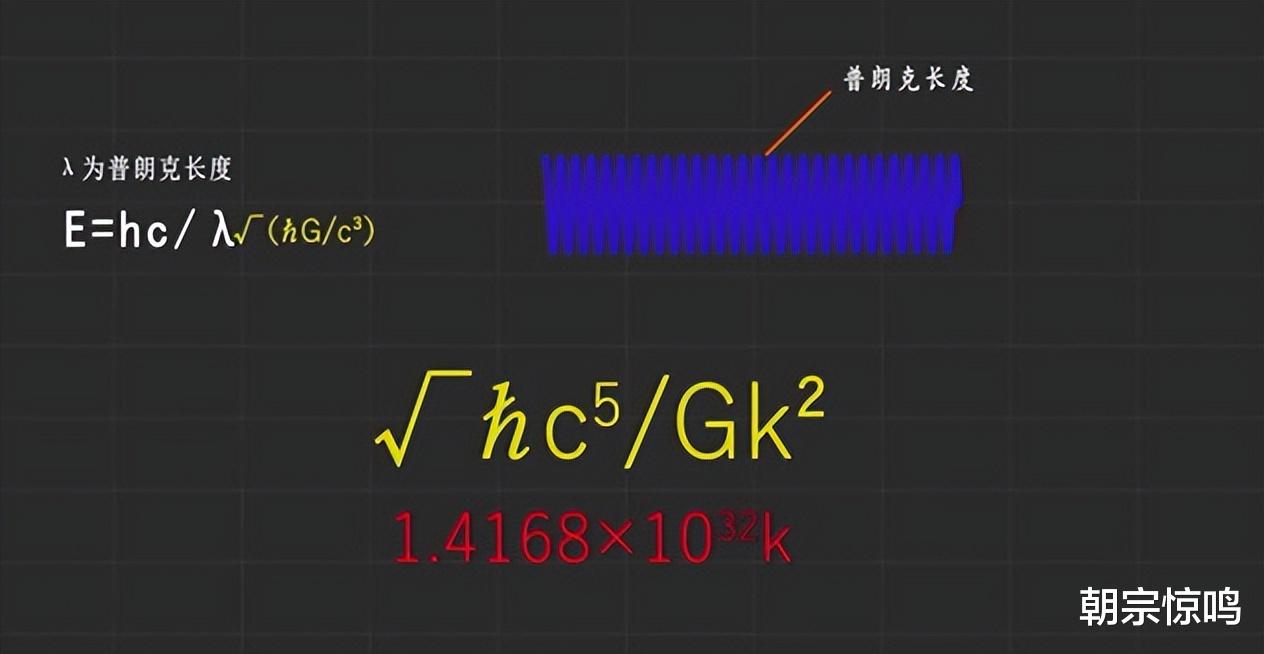
那么光子能量的最大值该如何计算呢?通过普朗克公式E=hν,我们就可以知道光子的能量和频率成正比。只要光子的频率不断增加,那能量就不断增加。而频率和波长成反比的话,光子的频率不断增加,波长就不断缩短。波长最短顶多到空间的最小尺度,这个尺度就是普朗克长度。所以,当光子波长缩短到普朗克长度,光子频率就越大,能量也就越大。通过普朗克公式E=hc/λ,波长λ的最小值为普朗克长度。
光子的能量的表达式E=hc/λ,普朗克长度是根号下c的三次方分之ħG。当光子波长为普朗克长度时,将其带入这里面,普朗克常数h等于2πħ。带入后,E等于2π根号下g分之ħG的五次方。这就是光子能量最大时的值。此能量下的温度也就是温度的上限,也就是普朗克温度。
由于麦克斯韦和波尔兹曼的贡献,我们可以得出能量和温度之间具体的线性关系。能量等于波尔兹曼常数k乘以温度。所以此时普朗克温度就是这一能量除以波尔兹曼常数k。
得到的结果就是2π根号下gk²分之ħc的五次方。这里面约化普朗克常数ħ,光速c,万有引力常数g,波尔兹曼常数k都是基础物理常数。普朗克温度则是自然单位制中的普朗克单位。
说人话,就是普朗克温度的数值必须是被基础物理量常数导出。和基础物理成述任何无关的无量纲因素都需要剔除,所以必须剔除2π。剩下的就是普朗克温度的表达式。这里面呢,全部都是常数。大家自己查一下就可以算出普朗克温度为1.4168乘10的32次方开尔文,也就是1.4亿亿亿亿摄氏度。
宇宙大爆炸是从那个体积无限小的起点开始的。起点爆炸后的第一个瞬间,宇宙尺度会经过普朗克长度。所以这个时候宇宙的温度有可能到达过普朗克温度。但这也只是猜想。
