1、只列式不计算
①一批水泥共重3/4吨,运走它的1/3,还剩几分之几?
1-1/3
②桃树有140棵,比梨树的棵树多40%,比梨树多多少棵?
140÷(1+40%)×40%
或140-140÷(1+40%)均可
③桃树有140棵,比梨树的棵树多40%,梨树有多少棵?
140÷(1+40%)
④桃树有140棵,梨树比桃树多40%, 梨树有多少棵?
140×(1+40%)
以上几题错误率较高,最直接的问题就是部分学生对单位“1”已知用乘法和单位“1”未知用除法运用不熟练,还有的学生在用除法时没有找准对应量及其对应分率导致做错。
2、某商店同时卖出两件商品,每件各卖得60元,但其中一件亏20%,另一件赚20%,问这两个商店卖出这两件商品是亏本还是赚钱?
解析:成本=销售价÷(1+利润率)
60÷(1-20%)+60÷(1+20%)=125元
60×2=120元
125元>120元
亏本
3、加工一批机器零件,师、徒合做12小时可以完成。先由师傅加工8小时,接着再由徒弟加工6小时,共加工了这批零件的3/5。已知师傅每小时比徒弟多做10个零件。这批零件共有多少个?
解析:师傅加工8小时,接着徒弟加工6小时,可以看成师徒合作6小时,然后师傅单独加工2小时
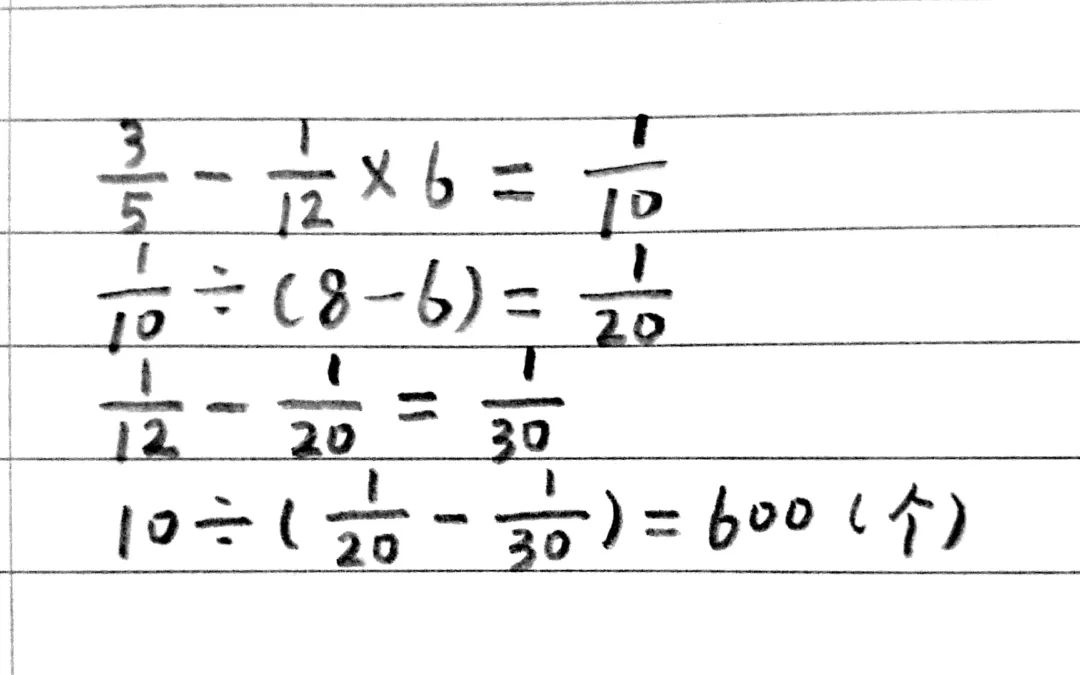
4、从甲班调10%的人到乙班, 两班人数相等。下列说法中,正确的是( )
A.甲班的人数比乙班多20%;
B.乙班的人数比甲班少20%;
C.甲班的人数比乙班多10%;
D. 乙班的人数比甲班少10%。
解析:本题可以借助以前的一个情境来理解,“甲给乙10支铅笔后,甲乙铅笔数相等,原来甲比乙多几支铅笔?”,这个问题都知道答案是甲比乙多两个10支也就是多20支铅笔,迁移到这题,甲调10%给乙就相等,甲看做单位“1”,说明甲原来比乙多2个甲的10%,也可以说乙比甲少20%,选择B。A选项单位“1”是乙,应该说成甲比乙多25%。
5、1000g哈密瓜在新疆测得含水量是99%,运抵南京后测得含水量为98%。哈密瓜运抵南京后还剩多少克?
解析:哈密瓜作为水果,构成分为两部分:水分和果肉,本题要抓住果肉不变,先求出果肉重,再用果肉重除以后来的果肉占的分率即可求解。
1000×(1-99%)÷(1-98%)=500克
6、甲、乙两人各有钱若干,现有2400元资金,如果全部给甲,则甲的钱是乙的2倍;如果全部给乙,则乙的钱是甲的3/2。 问原来两人各有多少元?
解析:本题要抓住总和不变(甲+乙+2400),可以利用量率对应,也可以利用比(量份对应),推荐下面两种解法:
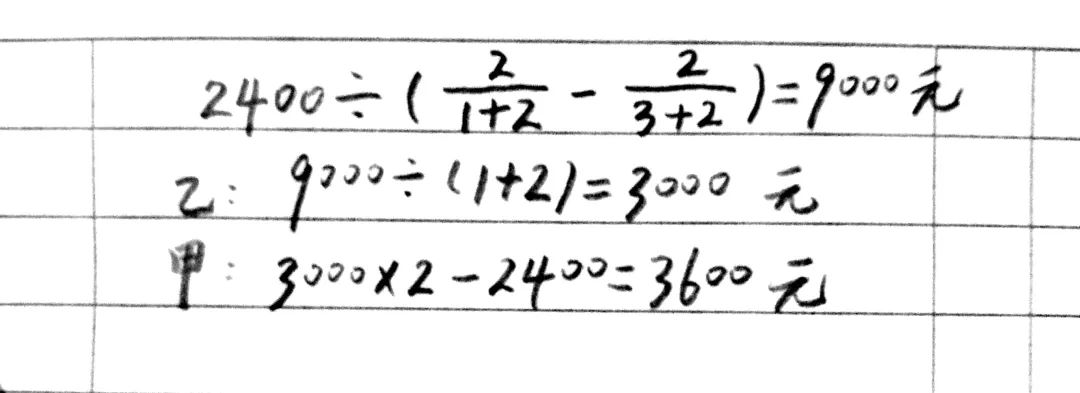

7、一艘观光船顺水每小时行6千米,逆水每小时行3千米,往返的平均速度是( )千米。
A.4.5
B.2
C.5
D.4
解析:本题很多学生不假思索直接用(6+3)÷2=4.5,从而错误地选择了A,平均速度不等于速度的平均,往返平均速度=往返总路程÷往返总时间,推荐以下两种思路,一种是假设一个具体路程数,还有一种是把单程看做“1”,选择D。
方法①
假设两地距离6千米
(6+6)÷(6÷6+6÷3)=4千米
方法②

8、一个正方形边长减少20%,则它的面积减少( )。
A.20%
B.64%
C.1/5
D.9/25
解析:边长变成原来的4/5,则面积变成原来的4/5的平方,也就是16/25,面积少了9/25,选择D。

9、小王和小李合伙投资,年终根据每人的投资进行分红,小王取了全部的1/3另加9万元,小李取剩余1/3和剩下的14万元。问小王比小李多得多少万元( )。
A.2
B.3
C.4
D.5
解析:本题要注意两个1/3的单位“1”是不同的,最终是利用倒推法求解。
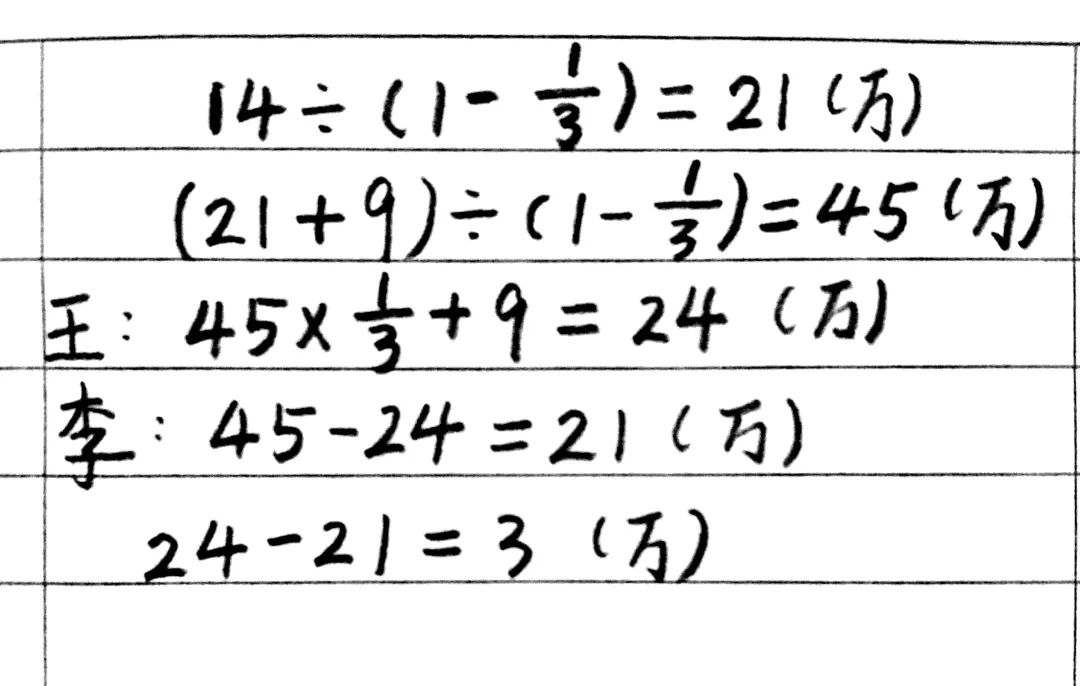
10、一个等腰三角形底和高的比是8: 3,把它沿底边上的高剪开,拼成一个长方形,这个长方形的面积是192平方厘米,长方形的周长是多少厘米?
解析:示意图如下
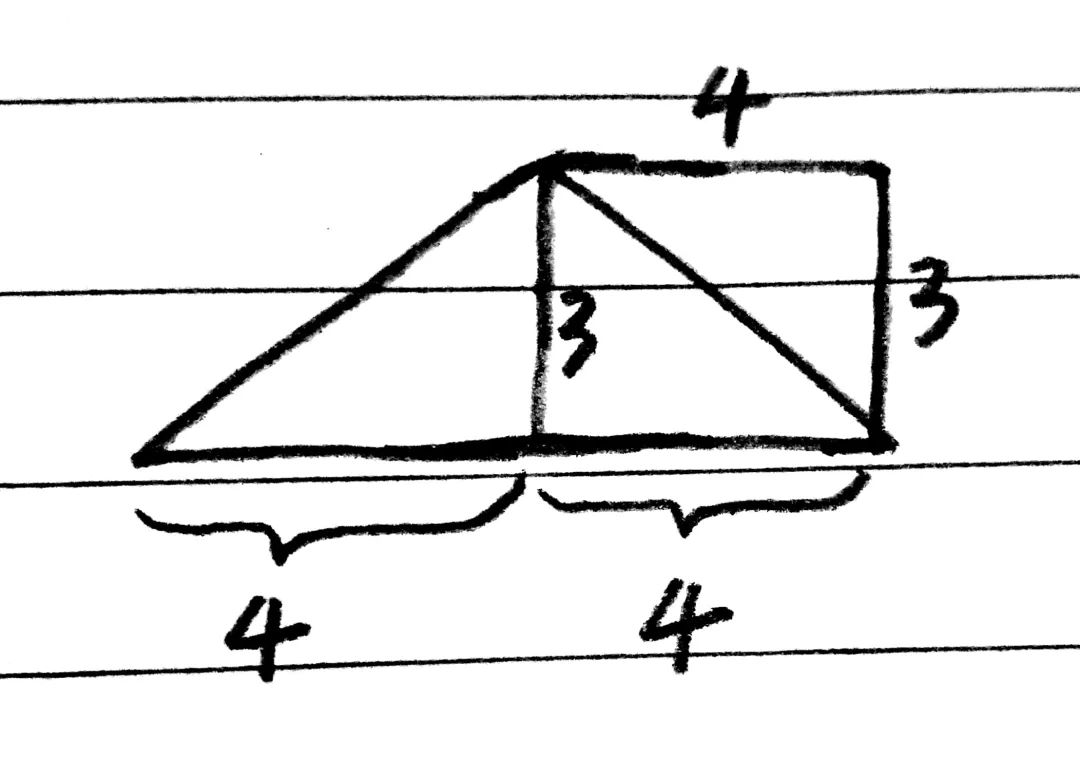
本题把长方形的长宽比求出后,可以把长看做4a,宽看做3a,4a×3a=12a²=192,即可求出a的值,进而求解。
8÷2=4厘米
4×3=12
192÷12=16
16=4²
长:4×4=16厘米
宽:3×4=12厘米
周长:(16+12)×2=56厘米
11、如下图,AD=3BD, BF=1/4BC,AB=1/4EC,如果三角形DEF的面积是60平方厘米,那么三角形ABC面积是多少?

解析:本题关键是能根据三角形三条边上不同的等分点求出三个空白三角形的面积占三角形ABC面积的分率,最终求出阴影三角形面积占三角形ABC面积的分率,利用量率对应求解。

12、明明和亮亮各有一些邮票。明明说:“你的邮票张数是我的3/4。”亮亮说:“如果把你邮票的1/3送给同学后,我就比你多5张了。”明明和亮亮原来各有多少张?
解析:推荐两种思路,一种是量率对应(明明的张数看做单位“1”),一种是比的知识也就是量份对应,先求出一份量,再乘以各自的份数。

13、《中华人民共和国个人所得税法》第14条规定,个人月收入超过5000元为应纳税所得额,并按下表方法纳税:

14、小冬爸爸每月工资是80000元,他每月应缴纳个人所得税多少元?刘经理每月缴纳个人所得税490元,他每月税后所得的工资是多少元?
解析:刘经理的490元税是两个税率段的税收之和,可以从中减去级别1中的90元税收,算出级别2中的税收,然后根据量率对应算出此税率段中的收入,再把两段收入再加上免税额度5000,最后减去税收即可求解。
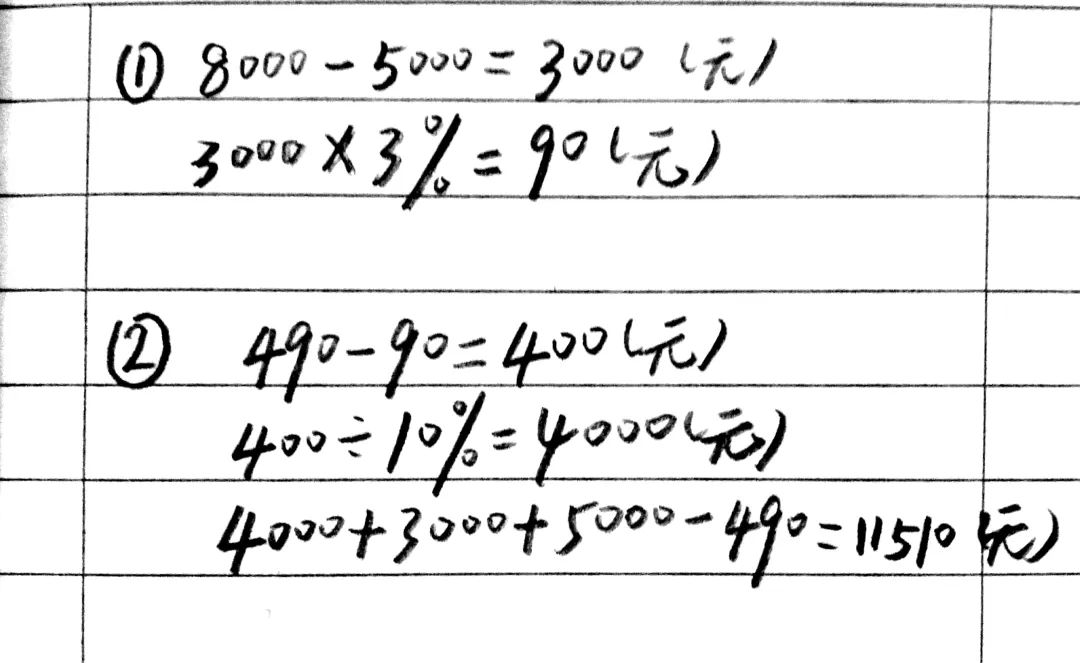
15、甲数是乙数的80%,乙数比丙数多20%,甲乙内三个数的比是( )。
解析:本题属于两个分比化成连比,关键是根据“是百分之几”和“多百分之几”求出两两之比,最后通过两两之比,依据比的基本性质化成三个量之比

16、木器加工厂有98名工人,每个工人平均每天能加工10张课桌或15把椅子,为满足市场需求,必须1张桌子与2把椅子配套发货。如果你是厂长应安排多少名工人加工课桌,多少名工人加工椅子才能保证成套供货而不会造成浪费?
解析:推荐两种解法,一种是比,一种是方程。
方法①:比
根据题意,一张课桌需要1/10人,一把椅子需要1/15人
方法②:方程
等量关系:课桌数×2=椅子数

17、科学研究发现,当人的下肢长与身高的比值为0.618时看起来最美。如果某成年女士身高153cm,下肢长92cm,那么该女士的高跟鞋鞋跟的最佳高度约为厘米? (精确到0.1厘米)
解析:本题关键是抓住上身高度不变,上身与身高的比值应该为0.382。
153-92=61厘米
61÷(1-0.618)≈159.7厘米
159.7-153=6.7厘米
18、一本书定价12元,售出后可获利定价的50%, 如果按照定价的八折出售,可获利( )元。
解析:利润=售价-成本,所以先要求出成本。
12×50%=6元
成本:12-6=6元
定价八折:12×80%=9.6元
利润:9.6-6=3.6元
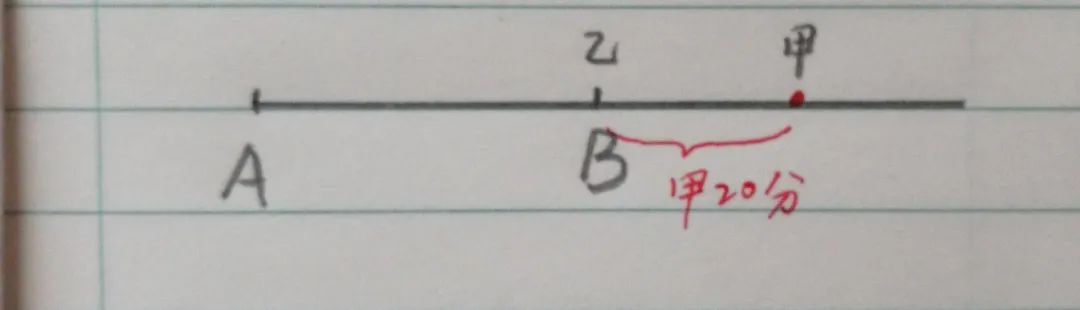
19、甲乙两人骑车从A地同时出发同向而行。甲每小时比乙快3千米,甲比乙早20分经过途中B地,当乙到达B地时,两人相距5千米,AB两地多少千米?
解析:推荐两种解法,核心都是利用路程差÷速度差=时间,再用时间×速度=路程。
①甲的路程就是AB距离
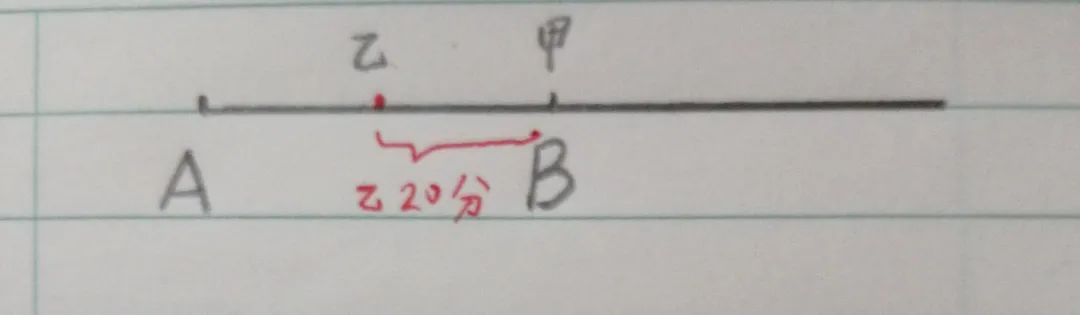

②乙的路程就是AB距离