可能会感到奇怪，洗扑克牌跟数学奥秘有何干系？答案是，确实有相当干系。这里小编简单介绍一本即将出版发行的新书，你也许就知道有多大的干系。

这本书的书名就叫：《洗牌的数学》（The Mathematics of Shuffling Cards），这本书探讨了洗牌与一些高等数学理论之间的联系，包括与李论、代数拓扑、超平面几何、随机微积分、数论等等。它提供了一个有趣的桥梁，了解如何应用概率论以及通向高等数学的许多不同领域。

这本书由美国数学学会（American Mathematical Society，AMS）将于六月正式出版发行，小编有幸浏览了该书的电子版。这里对这本书做简单介绍。

简单的来讲，这本书告诉你，数学如何可以回答一个古老的洗扑克牌的问题，即一副纸牌需要洗多少次才能确保牌完全混合。它可以揭示洗牌与发牌的最佳方法。

本书作者为著名数学家、斯坦福大学数学与统计学教授、佩尔西・戴康尼斯（Persi Diaconis），和南加州大学多恩西夫文学、艺术与科学学院的数学教授、杰森・富尔曼（Jason Fulman）。

在具体介绍这本书之前，有必要先简单介绍一下书的著者之一戴康尼斯，一位传奇式的人物。他14岁离家与魔术传奇人物戴·福农（Dai Vernon）周游世界表演扑克魔术，他从乔治华盛顿高中辍学后老师给他的成绩获得了高中文凭。24岁时回到学校学习数学，钻研了数学家威廉·费勒 (William Feller ) 著名的《概率论及其应用概论》两卷本论著。就读于纽约城市学院本科，1971年毕业获得博士学位。1974年取得哈佛大学数理统计学博士。

其夫人、苏珊·福尔摩斯（Susan P. Holmes），也是著名统计学家、斯坦福大学教授，她在将非参数多元统计、引导方法和数据可视化应用于生物学方面的工作而闻名。

这本书是戴康尼斯几十年的扑克生涯、25年的学术研究的结晶。他解决了一系列关于随机性的学术问题，包括掷币和洗牌。1992年，他和合作者证明了完美洗牌至少要洗七次。他又和合作者证明了掷币哪面向上，物理因素比运气要重要得多。他发表了几十篇有关论文、著有多本书，其中《神奇的数学：激发伟大魔术的数学思想》（普林斯顿大学出版社，2012 年）获得2013年欧拉图书奖。

好了，因篇幅期间，这里不再详细讲述作者动人的传奇故事。书归正传，回到对这本书的简单介绍。

这本书首先给读者的深刻印象就是：洗牌是一种数学。比方说简单的数学问题，洗好一副牌，一副52张的扑克牌，所需的理想洗牌次数应该是多少？洗牌与具体所使用的牌局类型有什么样的联系？我们许多人知道，常见的洗牌有下面几种扑克洗牌方法：

翻页洗牌法（riffle shuffle），或称鸽尾式洗牌：将一副扑克牌大致分成两半，然后用拇指快速穿插，如翻书一样，是一种常用的有效洗牌法，如下图所示。理论上，一副扑克牌需要七次洗牌能很好地混合一副牌。

平滑混洗法（smooshing shuffle）：将扑克牌平摊在桌子上，然后将它们随机彼此平滑混合，故称“smooshing”，如下图所示。理论上，一副扑克牌需要 30 到 60 秒钟的时间才能彻底混合。

（注：上面动画图中示范者为本书著者之一、富尔曼教授）

过手洗牌法（overhand shuffle）：取一叠叠牌的一部分并将它们移动到新的叠牌中，如下图所示。理论上，一副扑克牌需要必须重复多达一万次才能很好地混合牌。

一般来讲，一副扑克牌混合得好与坏，取决于什么样的扑克牌局。譬如说，对于21点牌局来讲，由于牌10、J、Q、K皆为同一种牌，那么这几种牌的洗牌后的顺序没差别，这样，从理论上将，一副扑克牌只需要4-5次洗牌能很好地混合洗一副牌。

我们许多人都知道有一种扑克魔术，可以将一副牌洗牌恢复到原来的顺序，这成为完美洗牌（perfect shuffle），或称：完全洗牌、全混洗、最佳洗牌等。

与上面完美洗牌类似的还有特定序列洗牌法（specific sequences shuffle），或称：特定序列混洗，将牌洗到所需的位置，从而魔术师能够以一种看似神奇的方式巧妙控制牌。

该书还从数学上探讨了扑克牌局的公平性，如何确保纸牌游戏中发牌的公平。

两种常用的发牌方法：一种是循环法（cyclic method），一种是来回法（back-and-forth）。在循环法中，扑克牌按循环法顺序发牌，例如座位一、位二、位三、位四、然后位一、位二、位三、位四。来回法发牌使用交替的方向，例如位一、位二、位三、位四，然后是位四、位三、位二、位一，如下图所示。

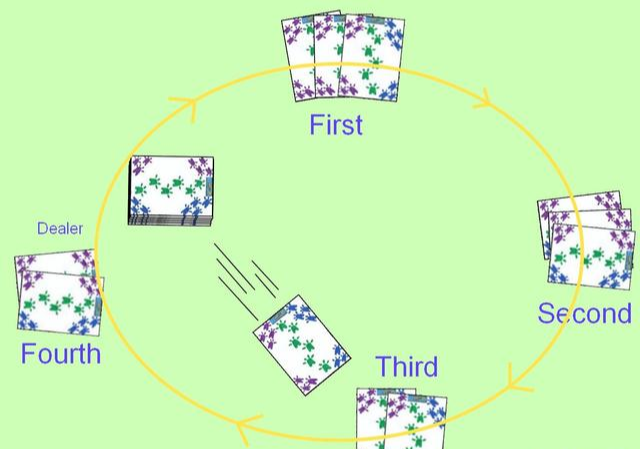
数学证明，来回法发牌速度更快，并提高了牌的随机性，因此对于混合良好的牌组只需要更少的洗牌次数。

洗牌的数学应用在纸牌游戏、魔术和赌博之外还具有其它重要的、实际科学技术应用。

分析洗牌的混洗的混合时间有助于计算机科学家确定数据库中文件和文件夹的最佳分布。生物学家运用洗牌数学混洗的混合时间来研究基因的顺序，这可以帮助生物学家评估两种生物之间的进化差距。

洗牌的数学与一种称为耐心排序（Patience Sort）的计算机科学理论有密切联系，如上图所示。耐心排序是将数组的元素分类成很多堆再串接回数组的一种排序算法，其命名正是来自于洗牌的数学。这种算法的变体有效地计算给定阵列中最长的增加子序列的长度。譬如描述客运航班的登机，研究人员通过洗牌数学以期了解和改善旅客耐心排序的交通流量。

在书中著者谈到洗牌推测性的应用是研究交通。如果你想象两条车道的汽车，汽车有时会相互交错，所以你可以把它们想象为平滑混洗法中拖来拖去的牌。

这本书还告诉我们说，洗牌数学中还存在一些一直难以解决的的问题，数学家们仍然对洗牌数学的这些问题感到困惑。

作为拉斯维加斯赌场特聘洗牌顾问，本书作者想知道使用拉斯维加斯赌场采用的所谓“近乎完美”的洗牌技术，即彻底混合一副牌所需的洗牌次数，按赌场说法需要执行“干净”的翻页洗牌法洗牌，两只手如何“近乎完美”地交替。这对数学家来说还是个难题。

数学家们还对最优猜测策略（optimal guessing strategy）感到困惑，即在一系列洗牌后翻开一张牌时最大化地正确猜测的预期数量。这个问题的答案无论对于扑克玩家、还是赌场管理人员都很感兴趣。对于扑克玩家，希望能够正确评估出尽可能多的牌；而对于赌场管理人员，希望的是，如何最有效地洗牌使玩家尽可能困难地评估要出的牌。

本书作者表示说，如果有足够的时间，他们相信很可能会解决这些以及许多其它洗牌难题。

读了这本书，会使人感到，原来扑克洗牌中竟然有这么有趣的数学与高深的奥秘，这也是作者写这本书的原因，想与他人分享洗牌与数学及其它不同领域的奥妙关系。