封面|万数归一
大家好,我是科学羊🐑。
你是否曾想过,一个再简单不过的数字游戏,竟然能让最聪明的数学家们困惑不已?
今天我们要聊的,就是这样一个谜题——考拉兹猜想,又称奇偶归一猜想、3n+1猜想、冰雹猜想等。
让我们从一个简单的规则开始。考拉兹猜想的规则简单到令人惊讶:选择任意一个正整数 N。
如果 N 是偶数,将它除以 2。
如果 N 是奇数,将它乘以 3,再加 1。
不断重复这个过程,直到最终你得到 1。
就这,听起来很简单,对吧?
似乎无论从哪个数字开始,这个过程最终都会收敛到 1。那么问题来了,这真的适用于所有的正整数吗?

我们先从一个小的数字 6 开始:
N = 6:
6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
一切顺利,6 最终确实变成了 1。N步骤中最高的数是16,共有8个步骤。
再试一个稍微大一点的数字,比如 19:
N = 19:
19 → 58 → 29 → 88 → 44 → 22 → 11 → 34 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
你看,无论是 6 还是 19,最终都不可避免地回到了 1。
N = 27:
数字太长了,我们就不列举了,看图就好。
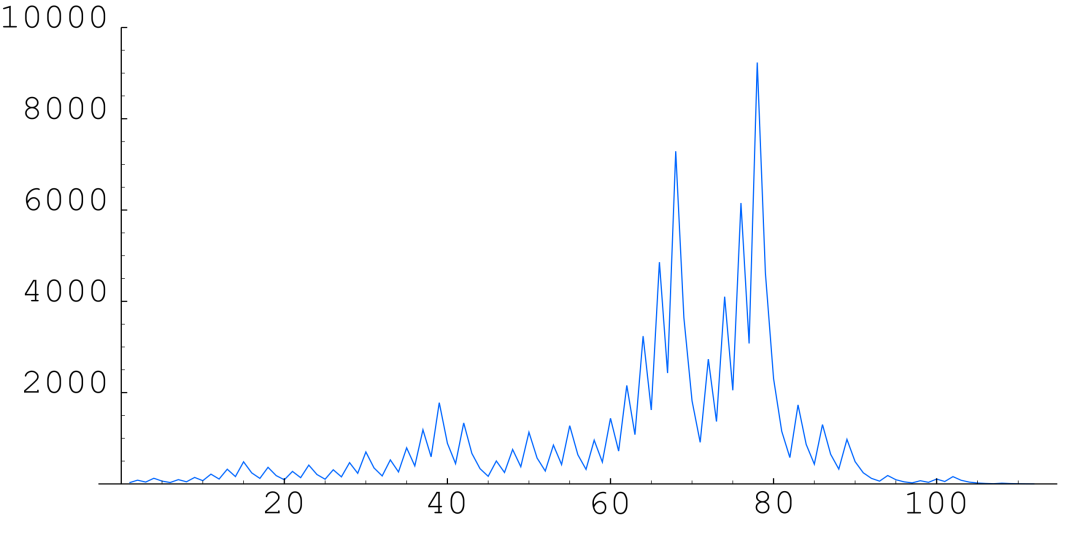
n=27时的序列分布(横轴-步数;纵轴-运算结果)
问题来了:真的这么简单吗?虽然目前看来无论测试多少个数字,都会陷入这个 4→2→1 的循环,但数学家们却无法证明,这种规律适用于所有的正整数。
数学家们已经用计算机验证了数万亿个数字,甚至计算到了 2^68 这个天文级别的数字,结果都指向 1。
但问题是,这并不是一个严格的数学证明。计算机只能验证有限的数字,而数学证明需要无穷的覆盖面。
为什么这么难?考拉兹猜想表面上看似乎是一道连中学生都能理解的问题,但它真正的难点在于如何用严密的数学逻辑证明它在所有正整数上都成立。
就像一座悬在数学家头顶的高山,仿佛已经看到了山顶,却始终无法抵达。
传奇数学家保罗·埃尔德什(Paul Erdős)在谈论考拉兹猜想时曾说过一句著名的话:“数学还没有为这样的问题做好准备。”
当一位历史上最伟大的数学家都发出这样的感叹时,我们就知道,这个问题远没有想象中简单。
考拉兹猜想看似只是一个关于数字的游戏,但它的本质却隐藏着数论和动力系统的深刻哲理。
你可能听过那句“蝴蝶扇动翅膀可以引发一场飓风”。
考拉兹猜想也是如此,微小的数字变化,最终却可能引发完全不同的结果,或者说看似规律却又充满不可预测性。
数学家们想要的不仅仅是一个经验性的结论,而是一个能解释为什么考拉兹猜想成立的完整数学框架。这正是难题所在。
不过,数学界从未停止努力,因为他们相信,一旦解决了考拉兹猜想,将带来数论甚至整个数学领域的新突破。
也许,在未来的某一天,这个谜题会由一个普通的数学爱好者,甚至是一个偶然提出新思路的年轻学生解决,又或者是AI...

无聊
色即是空
JYYX
这题很难,类似歌德巴赫猜想。但这结论貌似本身没啥用。所以研究的人很少。
Shooting Quasar
[得瑟]对奇数一通操作过后会得到2的高次幂,然后就回到1了。。