当高斯于1855年去世后，留下的文件中有大量未发表的数学文章，其中就有高斯支持波尔约和罗巴切夫斯基关于非欧几何的证据。当这些文件被逐步发表以后，人们才真正意识到波尔约和罗巴切夫斯基究竟研究了些什么。

相当偶然的是，高斯在哥廷根有一个学生能够革命性地把非欧几何向前推进，这个学生就是黎曼。1854年他被召来作就职演说答辩。黎曼按照当时的习惯提出了三个演说题目，而高斯作为主试人选取了黎曼最不希望的题目∶《论作为几何基础的假设》。这篇论文直到黎曼去世以后才在1867年发表，它对于几何学作了完全的重新陈述。

黎曼提出，几何学就是对他所说的流形的研究。这些流形是点的“空间”，并附有距离的概念使之在小尺度上就像是欧几里得距离，而在更大的尺度上可以大不相同。他建议，这种几何学可以利用微积分来研究，可以对任意维的流形作研究，事实上，黎曼甚至准备思考维数为无穷的流形。

黎曼的几何学的一个非常本质的方面就是它只研究流形的内蕴的性质，而不问那些依赖于如何嵌入在更大的空间里的方式，在这一方面，他是完全遵从高斯的。 特别是，两点x和y的距离定义为连接这两点的完全位于此曲面上的曲线的最短的距离。这个曲线称为测地线（在球面上，测地线就是大圆弧）。

甚至2维流形也各有各的不同的内蕴曲率（即令单独一个2维流形在不同点也有不同的曲率），所以黎曼的定义，在每一个维数上，都引导到无穷多个真正不同的几何学。此外，最好的是这些几何学的定义不需要参考包含它们的欧几里得空间，所以，欧几里得几何学的独断的地位被一劳永逸地打破了。

黎曼就职演说标题中的“假设”一词说明他对欧几里得所需的公设毫无兴趣。他对于欧几里得几何学与非欧几何学的对立也没有多大兴趣。他在这篇文章开始处只是稍稍提到，尽管有勒让德的努力，几何学心脏里还有一点模糊之处，而在文章末尾，黎曼考虑了在2维常曲率流形中的三种不同的几何学。他注意到，其中一种就是球面几何学，另一种是欧几里得几何学，而第三种则又不相同；在每一种情况下，只要知道到了一个三角形的内角和，就可以算出所有三角形的内角和。

但是。 黎曼没有提到波尔约和罗巴切夫斯基，只是说如果空间的几何学真是常曲率的3维的几何学，则想要确定究竟是哪一种几何学，就需要在极其广袤的区域里作量度，而区域之大又使得这种量度是办不到的。他讨论了把高斯的曲率推广到任意维空间，而且指明了在常曲率空间里度量（即距离的定义）应该是什么。 他写出的公式非常广泛，但和波尔约以及罗巴切夫斯基的情况一样，其中含有一个实参数——即曲率。如果曲率为负，黎曼的距离定义就会给出非欧几何学。

1866年黎曼去世，而当他的就职演说发表时，一个意大利数学家贝尔特拉米已经独立地接近了他的某些思想。贝尔特拉米感兴趣的是，如果把一个曲面映为另一个曲面，会有哪些可能性。例如可以对一个特定的曲面S问，能否找到一个映射把S映到平面上，而且使每一条测地线都被映为一条直线？他发现，这当且仅当空间有常曲率时才可能。例如从半球面到平面就有一个著名的映射具有这个性质。贝尔特拉米找到一个简单的方法稍微修改一下公式，使它定义一个从常负曲率曲面到圆盘内域的映射，而且他认识到这样做的意义∶他的映射在圆盘内域定义了一个度量，而所得的度量空间服从非欧几何的公理，所以，这一组公理不会导致矛盾。

其实，在德国，数学家明定早几年就找到过这样一个具有常负曲率的曲面，他称此曲面为伪球面（pseudosphere），是由一条称为曳物线的曲线绕自己的轴旋转而得的。这个曲面形状像喇叭，看来与欧几里得平面比较起来颇不自然。几年以后，伪球面又由刘维尔独立地重新发现，而法国数学家柯达齐也从这个来源得知了这个曲面，并且发现其上的三角形服从双曲三角学。但是这些人没有一个看到它与非欧几何学的联系，这要有待于贝尔特拉米了。

贝尔特拉米认识到，他的圆盘描述了一个常负曲率空间，在其中罗巴切夫斯基几何学为真。他看到他的圆盘与伪球面的关系，可以说是类似于平面与无限圆柱面的关系。经过一段时期的怀疑以后，贝尔特拉米学到了黎曼的思想，而且认识到他的圆盘就是非欧几何的空间的最好不过的描述，没有必要再去把他的几何学实现为3维欧几里得空间的某个曲面上的几何学。 于是，他在1868年发表了自己的论文。这是我们可以称呼为非欧几何这个数学领域的坚实基础第一次公开问世。

贝尔特拉米

1871年，年轻的克莱因也开始投身到了这个学科。他知道英国数学家凯莱正企图把欧几里得度量引入射影几何。当克莱因还在柏林学习时，他就想要推广凯莱的思想，把贝尔特拉米的非欧几何学也纳入射影几何学为其特例。他的思想遭到魏尔斯特拉斯（当时柏林的领头的数学家）的反对，理由是射影几何学不是度量几何学，所以，他宣称，射影几何学不能产生度量概念。

但是克莱因坚持下来了，而且在1871-1873三年的三篇文章里证明了所有已知的几何学都是射影几何学的子几何学。他的思想是把几何学重新铸造成为对于作用在空间上的某个群的研究。图形（即空间的某个子集合）的在此群作用下不变的性质就是几何性质。所以，例如对于某一维的射影空间，适合于射影几何学的群就是所有映直线为直线的所有线性变换的群，而其中把某一给定的圆锥映入此圆锥内域的线性变换所成的子群，就可以看成非欧几何的变换群。

交比和圆锥内的距离。 平面的射影变换把同一直线上的 4 个不同点A，B，C，D 映为另外 A'，B'，C'，D'，而且保持

不变，即

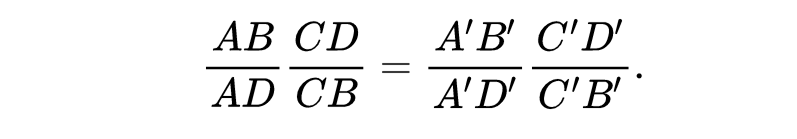
这个量称为A，B，C，D4点的交比，并且记为CR（A，B，C，D）。

1871年，克莱因把非欧几何描述为在一给定的圆锥 K 内之点的几何学，它所允许的变换是把K映为自身，内域映为内域的射影变换。

克莱因的非欧几何的射影模型中一条直线上的三点 P，Q，R

为了定义 K 内两点 P，Q 的距离，克莱因注意到如果把直线 PQ 延长到与 K 相交于 A，D 两点，这时，交比 CR（A，P，D，Q）在射影变换下不变，就是说，它是一个射影不变量。 此外，若R是直线PQ上的第三点，而其次序为P，Q，R，则CR（A，P，D，Q）CR（A，Q，D，R）=CR（A，P，D，R）。依照此式，克莱因定义两点P，Q的距离为

按照这个定义，沿一直线的距离是可加的，d（PQ）+d（QR）=d（PR）。

19世纪70年代，克莱因的研究成果是由他的上述文章中的第一和第三篇传递的。 这些文章发表在当时新创办的刊物《数学年刊》上。随着克莱因名声的增长，情况有了改变，到19世纪90年代，当他把第二篇文章重新发表，著名的埃尔朗根纲领才广为人知。埃尔朗根大学就是克莱因当了教授的大学，当时克莱因非常年轻，只有23岁。 但是它并不是克莱因的就职演说。有好多年，埃尔朗根纲领这篇文章还是奇怪地少为人知，看来，当时这篇文章对数学的影响并不像有些历史学家认为的那样。

非欧几何学把人们的注意力从几何图形引向了那些在关键方面不改变这些图形的变换。例如，欧几里得几何中，重要的变换有我们熟悉的旋转和平移。这些变换相应于刚体的运动，而当代的心理学家认为，人们正是通过刚体运动来认知周围的空间的。但是这个理论在哲学上是颇有争议的，特别是在它有可能被推广到另一种度量几何学，即非欧几何学时也是如此。因此，克莱因小心地把自己的数学论文标题定为《论所谓非欧几何学》，以安抚持敌意的哲学家们（特别是哥廷根的很有地位的康德哲学家罗泽）。

但是，克莱因的这些文章和贝尔特拉米以前的工作已经提出了充分的论据、几乎所有的数学家都被说服了。他们相信除了欧几里得几何学以外，现在还有一种同样有效的数学系统，称为非欧几何学，至于要问哪一个在空间中是真的，似乎非常清楚，欧几里得几何学是明智之选，这也没有疑问，无需讨论了。

利普希茨证明了可以在这个新背景下让物质就放在这里，这样做出全部力学来，这只是一个有某种魅力的假设的情况，而除此以外就什么意外也没有了。当时居于领导地位的物理学家亥姆霍兹对此也有了兴趣，而且写了一篇文章论述空间应该是什么样的，才能在其中有自由的运动。他的第一稿有大错，因为他当时还不知道非欧几何学，但是当贝尔特拉米向他指出错误以后，他又写了第二稿。重写的文章在数学上仍有瑕疵，后来由李（lie）向他指出。但是，他马上就在哲学上遇到了麻烦。

他们的问题是∶“非欧几何学是一种什么样的知识？”康德哲学正在回潮，又成了一种时尚，而在康德看来，关于空间的知识是一种基本的纯粹先验的直觉，而不是要由实验来决定的事情∶没有这种直觉，就根本不可能有关于空间的任何知识。 面对着非欧几何这样一种对立的理论，新康德主义哲学家遇到问题了。他们可以同意，数学家们做出了一个新的冗长的逻辑练习，但它可能是关于世界的知识吗？难道不是肯定，世界不会有两种几何学吗？亥姆霍兹进行了反击，论争说，欧几里得几何学抑或是非欧几何学，都是以相同的方法获取到的（通过经验），但是这种经验主义的调门是哲学家们不能接受的，所以，直到20世纪初叶，非欧几何对于他们还是一个问题。

其实数学家们对于正在成为人们共识的立场，还不能给出完全严格的辩护，而当新闻传开，说是对于空间有两种可能的解释，因而不能断定欧几里得几何学一定是对的，这时，受过教育的公众，就提出问题了∶什么才是空间的几何学？按照这种新的提法来掌握问题的第一批人中就有庞加菜。他在19世纪80年代，由于在一系列了不起的文章中重新提出了贝尔特拉米的圆盘，并使之成为共形的（conformal），而在数学上得了大名声。所谓共形就是说非欧几何的角度和模型中的角度是相同的，然后就用新的圆盘模型把复变函数论、线性微分方程理论、黎曼曲面和非欧几何连接起来，生成了一个丰富的新思想的整体。

后来，在1891年庞加莱又指出，这个圆盘模型使我们能够证明非欧几何的任意矛盾必定导致欧几里得几何学里的矛盾，反之亦然。所以欧几里得几何学是相容的，当且仅当非欧几何是相容的。这件事情有一个奇怪的推论∶如果有什么人真正能从欧几里得几何的核心导出了平行线公设，那他们必然在无意之中证明了欧几里得几何学是不相容的。

要想确定是哪一种几何学描述了真正的宇宙，一个显然的方法是诉诸物理学。 但是庞加莱不相信这一点，他在另外一篇文章中论证说，对于经验可以有多种解释，没有一种合乎逻辑的方法能够决定哪些属于数学，哪些属于物理学。 举例来说，设想有一种精巧的量度图形内角和的方法，说不定是天文学尺度的图形。 这里需要取什么东西为直的，可能是取光线为直的。如果最终得出结论说三角形内角和小于两直角，而且其差的大小正比于三角形面积。庞加莱说，这时仍然有两个可能的结论∶其一，光线是直的，而空间的几何学是非欧几何学；其二，光线是曲的，而空间是欧几里得空间。他接着指出，进一步，没有一种合乎逻辑的方法来在这两种可能性里作选择。

这种哲学立场在20世纪好长一段时间里以约定论（conventionism）之名存在着，但在庞加莱的有生之年，远未被人们接受。约定论的一位著名批评者是意大利数学家恩里克斯，他的论据是，一个性质是几何性质还是物理性质，可以从我们是否对它有控制而定。我们不能改变引力定律，但是可以通过让物质运动而改变一个质点受到的引力。庞加莱曾经把他的圆盘比作一个金属圆盘，使其中心很热，而向外边运动时变冷。他曾经给出过一个冷却定律来产生和非欧几何同样的图形。恩里克斯回答说，热也是可以改变的东西。如庞加莱所应用的那种确实在我们控制之外的性质就是几何性质。

这个问题最终还是解决了。有两个人把数学推动得远远超过了庞加莱的简单的二分法。第一个是希尔伯特，他按照公理化的途径对几何学进行了广泛的改写，他的这项工作开辟了许多公理化研究的道路。希尔伯特的工作极其出色地获得了一个思想：如果说数学是坚固可靠的，那么来自它的推理的本质是坚固可靠的，这引导到数理逻辑的深刻研究。

第二个是爱因斯坦，他在1915年提出了广义相对论，它在很大程度上是引力的几何理论。数学的信念被恢复了，他们对于几何学的感觉大为扩大了，对于几何学和空间的关系的洞察也复杂多了。爱因斯坦充分地应用了关于几何学的现代观念，如果没有黎曼的工作，爱因斯坦的成就是不可思议的，他把引力描述为4维时空流形的一种曲率，他的工作引导到关于宇宙的大尺度结构以及宇宙的最终命运的新的思考方式，引导到至今仍未回答的问题。