这些由非常简单的方程定义的曲线笼罩在神秘和优雅之中。事实上，描述它们的方程非常简单，即使是高中生也能理解。

然而，尽管世界上一些最伟大的数学家做出了不懈的努力，仍有大量关于它们的简单问题尚未解决。但这还不是全部。正如你很快就会看到的，这个理论连接了数学的各个重要领域，因为椭圆曲线不仅仅是平面曲线。

在数学中，一些几何问题可以转化为代数问题，反之亦然。例如，看一下几千年前的一个经典问题，正整数n是否等于某个边长是有理数的直角三角形的面积，也就是说。在这种情况下，n被称为同余数。例如，6是一个同余数，因为它是边长为3，4和5的直角三角形的面积。1640年，费马证明了1不是全等数。自从费马的证明之后，证明某个数是（或不是）同余数的研究就一直在进行。

令人惊奇的是，我们可以用初等方法证明对于每一组有理数数（a，b，c），如果有

我们可以找到两个有理数x和y，使得

反过来，对于每个有理数对(x, y)使得y^2= x^3- (n^2)x且y≠0，我们可以找到三个有理数a, b, c使得a^2+ b^2= c^2和1/2 ab = n。

也就是说，当y≠0时，面积为n的直角三角形恰好对应方程y^2= x^3- (n^2)x的有理解，反之亦然。数学家会说这两个集合之间存在双射。

因此，当且仅当方程y^2= x^3- (n^2)x有一个有理解(x, y)且y≠0时，n＞0是同余数。例如，由于1不是同余数，y^2= x^2- x的唯一有理解是y = 0。

具体对应如下，

如果我们在边长为3，4，5，面积为6的三角形上尝试这种对应关系，那么对应的解是(x，y) =(12，36)。这非常不可思议的。一个人从数论和几何的问题开始，通过代数，把它转化成一个关于平面曲线上有理点的问题！

一般来说，如果f(x)表示具有非零判别式的三次多项式（即所有的根都是不同的），那么y^2= f(x)描述的是一条椭圆曲线，除了“无穷远点”（即椭圆曲线上点在加法运算下构成的群中的单位元）。

现在，通过一个小小的代数技巧，我们可以对坐标进行适当的（有理）改变，并得到一条形式为

的新曲线，使得两条曲线上的有理数点一一对应。从现在开始，当我们说“椭圆曲线”时，指的是y^2= x^3+ ax + b形式的曲线以及无穷远处的一点𝒪。此外，我们假定系数a和b是有理数。

椭圆曲线有两种典型的形状，如下图所示。

维基百科

然而，如果我们把x和y看作复变量，曲线看起来就完全不同了。它们看起来像是甜甜圈。

那么我们为什么要研究椭圆曲线，我们可以用它们做什么呢？

首先，许多数论问题可以转化为丢番图方程的问题，其次，椭圆曲线与被称为格子（lattices）的离散几何对象有关，并与一些非常重要的被称为模形式的对象密切相关，这些对象是一些极其对称的复函数，其中包含大量的数论信息。

实际上，椭圆曲线和模形式之间的联系是证明费马大定理的关键，安德鲁·怀尔斯在20世纪90年代通过几年的努力实现了建立了这种联系，从而证明了费马大定理。在密码学中，椭圆曲线也被用于加密信息和在线交易。

然而，它们最重要的特征是一个令人兴奋的事实，即它们不仅仅是曲线和几何。事实上，它们有一个代数结构叫做阿贝尔群结构，这是一种几何运算（规则），用来把曲线上的点相加。对于阿贝尔群，你可以把它想象成一组对象，对它们进行运算，使得它们具有与整数在加法方面相同的结构（除了它们可以是有限的）。

阿贝尔群的例子有：

关于加法运算的整数ℤ。

将正方形顺时针旋转90度的操作。

以向量为元素，向量加法为运算的向量空间。

椭圆曲线的神奇之处在于，我们可以在椭圆曲线上的有理数点（也就是说，x和y坐标都是有理数）之间定义一个运算（称它为“⊕”），这样曲线上这些点的集合就变成了一个关于运算“⊕”和单位元素𝒪（无穷远处的点）的阿贝尔群。

让我们定义这个运算。如果你在曲线上取两个有理点（例如P和Q），并考虑一条经过它们的直线，那么这条直线与曲线相交于另一个有理点（可能是无穷远处的点）。我们称这个点为-R。

现在，因为曲线是关于x轴对称的，我们得到另一个有理点R。

这个反射点（上图中的R）是前面提到的两个点（P和Q）的相加。我们可以写成

可以证明，这个运算是满足结合律，这真的很令人惊讶。此外，无穷远处的点作为这个运算的（唯一）恒等式，每个点都有一个逆点。

事实证明，两条不同的椭圆曲线可以有截然不同的群。一个重要的不变量，在某种意义上是最具定义性的特征，就是所谓的曲线（或群）的秩。

一条曲线上可以有有限个有理点，也可以有无限个有理点。我们感兴趣的是，需要多少点才能根据前面提到的加法规则生成所有其他的点。这些生成器被称为基点。

秩是一种维数度量，就像向量空间的维数一样，表示有多少独立的基点（在曲线上）具有无限阶。如果曲线上只包含有限数量的有理点，那么秩为零。仍然有一个群，但它是有限的。

计算椭圆曲线的秩是出了名的困难，但莫德尔告诉我们椭圆曲线的秩总是有限的。也就是说，我们只需要有限数量的基点就可以生成曲线上的所有有理点。

数论中最重要和最有趣的问题之一被称为波奇和斯温纳顿-戴雅猜想（the Birch and Swinnerton-Dyer Conjecture），它完全是关于椭圆曲线的秩。事实上，它是如此的困难和重要，以至于它成了千禧年难题之一。

在具有有理数系数的椭圆曲线上寻找有理点是困难的。一种方法是通过对曲线p进行模数化简，其中p是质数。这意味着，我们不考虑方程y^2= x^3+ ax + b的有理解集，而是考虑同余

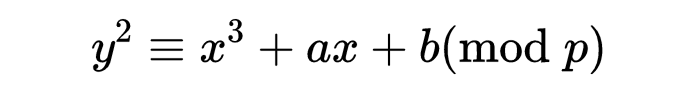
的有理解集，为了使它有意义，我们可能必须通过在两边乘以整数来消去分母。

所以我们考虑的是两个数，当除以p时余数相同，在这个新空间中相等。这样做的好处是，现在只有有限数量的东西需要检查。让我们用N_p表示对p取模的简化曲线的有理解的个数。

在20世纪60年代早期，戴尔在剑桥大学计算机实验室使用EDSAC-2计算机来计算在已知秩的椭圆曲线上取p模的点数。他和数学家布莱恩·约翰·伯奇一起研究了椭圆曲线，并在计算机处理了一堆下面形式的椭圆曲线之后

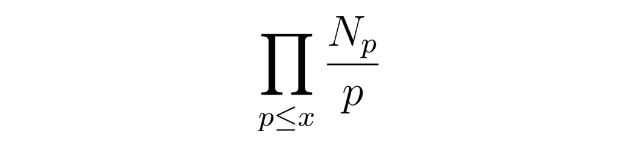
对于x的增长，他们从与曲线E相关的数据中得到以下输出：y^2= x^3- 5x（作为一个例子）。我应该注意到x轴是log log x，y轴是log y。

在这个图上，回归线的斜率似乎是1。曲线E的秩是1，当他们尝试不同秩的曲线时，每次都发现了相同的模式。拟合的回归线的斜率似乎总是等于曲线的秩。

更准确地说，他们提出了大胆的猜想

这里C是某个常数。这种计算机运算加上极大的远见，使他们对曲线的哈塞-韦尔L-函数L(E，s)在s = 1时的行为做出了一般性猜想。这个L函数定义如下。让

令曲线的判别式记为Δ。然后我们可以定义与E相关的L函数为以下的欧拉积

我们把它看做复变量s的函数。波奇和斯温纳顿-戴雅猜想现在是这样的：

设E为ℚ上的任意椭圆曲线。曲线E的有理点的阿贝尔群E(ℚ)的秩等于s = 1时L(E, s)的零点的阶。

之所以说它很有远见是因为，在当时，他们甚至不知道是否所有这样的L函数都存在所谓的解析延拓。问题是，上面定义的L(E, s)仅当Re(s)＞3/2。

它们都可以用解析延拓在s = 1处求值，这在2001年首次被证明，通过安德鲁·怀尔斯证明的与模形式的密切联系。有时这个猜想是用L函数的泰勒展开来表示的，但它是用不同的方式来表达同样的事情。有理数的领域可以被更一般的领域所取代。

椭圆曲线的是一场数论、抽象代数和几何之间的美丽舞蹈。关于它们，除了我在这里描述的，还有很多可说的，我希望你能感受到或看到一些令人震惊的东西。