本文的主题:微分方程(2):一阶微分方程及其定义
微分方程第一步,吃透基本概念——复数,多项式方程及矩阵理论

请点击输入图片描述(最多18字)
世界是一个微分方程,男人和女人只是变量。——Ben Orlin,《变化是唯一不变的:疯狂世界中的微积分智慧》
上一篇文章介绍了本系列中需要的先决条件和基础知识。本篇文章我们开始讨论一阶微分方程。
一阶微分方程
在物理现象建模中,微分方程在许多问题的求解中起着至关重要的作用。所有的物理学科中,都有其独特的物理情况,都要求你能写出必要的微分方程,然后解出它们。
一般来说,将一个未知函数与其各阶导数联系起来的方程就是微分方程。举两个例子:
u'=u
v''+tv’=t
方程组{x'=x+3y,y'=x-y}提出了确定同时满足两个方程的两个函数x(t)和y(t)的问题。
微分方程的解是一个满足方程在某个区间(α,β)上可微的函数。例如,u(t)= e^t对于所有t都满足u'=u,因为u'(t)= e^t,u(t)= e^t。因此,e^t被称为u'=0的解。
通常,用“基本”函数的组合来表示一个解是不可能的。下面对前面的例子做一个小修改:v'' +tv=t。在这些情况下,我们用其他方法来表示微分方程的解。这些方法包括表格、函数图或幂级数的形式。
定义
对于常微分方程(ODE),其中的因变量(未知函数及其导数)是一个自变量(因变量所依赖的量)的函数。
偏微分方程(PDE)是因变量为一个以上自变量函数的微分方程。如拉普拉斯方程:

其中因变量是u(x,y)。
因变量通常用来表示物理问题中所要求的未知量或与之密切相关的量。例如,如果想知道飞机机翼上的升力,根据流体力学的定律,可以列出具有未知函数的偏微分方程,未知函数是速度函数v(x,y,t)。如果v(因变量)可以被求出,那么我们就可以计算出机翼上的升力。
微分方程的阶数是出现在方程中的未知函数的最高阶导数。如下面方程的阶数是3

t^4和u^5的出现与确定方程的阶无关。
我们考虑一类重要的特殊方程,如果它们可以写成以下形式之一,则称为线性方程
一阶:u'+p(t)u=f(t)
二阶:u''+p(t)u'+q(t)u=f(t)
一般的n阶线性方程是

非线性的方程就是非线性的。方程

是非线性的,就像u''+sin(u)=0和u'+u^(1/2)=0。如果n阶线性方程中的f(t)=0,则该微分方程为齐次方程,否则就是非齐次的。你也应该注意到,

是标准形式:最高阶导数的系数是1,所有不包含因变量的项都在右边。
有些线性方程特别容易解。例如,一阶非齐次方程

有无穷多个解:

每个解对应一个常数K。三阶方程:u'''=0的解是:
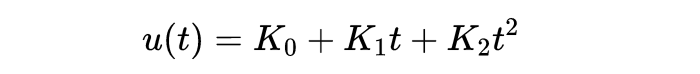
三个任意常数K_0,K_1和K_2是积分常数。
每一个线性常微分方程都有一组解。特解是通过对解的条件进行补充来确定的。
假设b_1,b_2,…,b_n是n个固定实数。n阶线性常微分方程的初值问题由下式给出

注意以下重要要求:
t_0是施加所有初始条件的自变量的值。
初始条件和微分方程的阶数一样多。
如果t的值有多个,则会产生一个边值问题。对于二阶线性常微分方程,边值问题是

一般来说,边值问题比初值问题更难解决。
注意,如果方程的解被限制在区间(α,β)内,那么我们总是假设点t_0和t_1在(α,β)内。
我们通常假定t_o=0。这不是一个严格的限制,因为总有可能将自变量从t变换到τ,使t=t_0对应于τ=0。这是通过定义τ=t - t_0来实现的。然后dt = dτ,并且
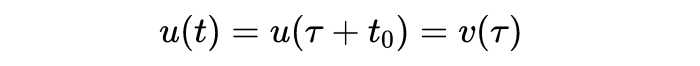
定义了一个新的未知函数v(τ)。因此,u(t_0)=v(0)=b_1,根据链式法则,

我们现在可以写出由这个方程给出的初值问题

为

本文介绍了微分方程的定义和基本特征。后面的文章将介绍不同类型的微分方程、定理和推论。

元道
[点赞]