数学中的一个常见主题是将在一个领域内有效的概念扩展到更大的领域。例如，利用伽玛函数将离散的概念扩展到连续的概念，或者用极限将有限的概念扩展到无限的，或者用矩阵将二维的概念扩展到任意维。

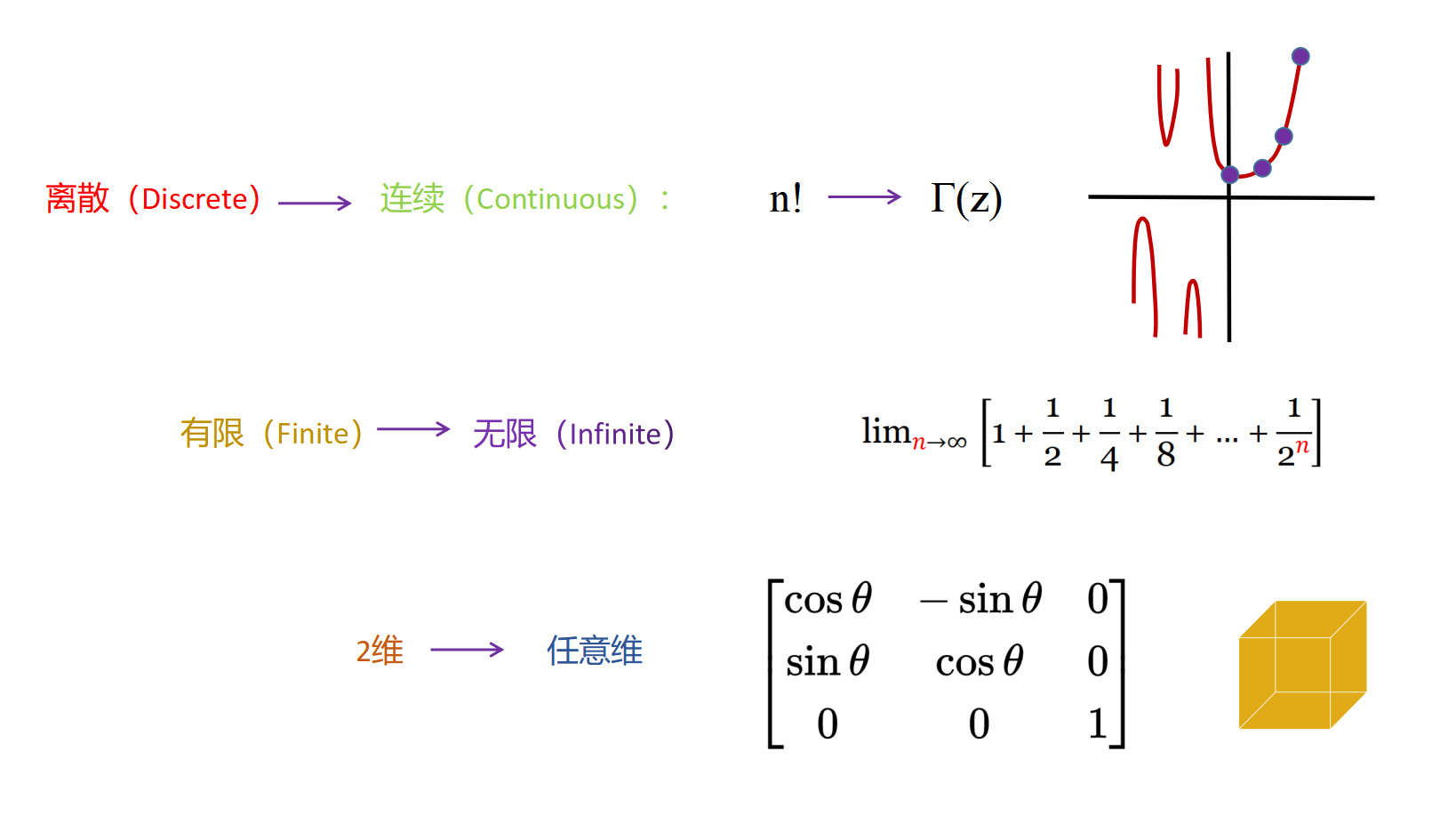
每当这种扩展成为可能时，总会让人兴奋不已，因为你会感觉你正在发现隐藏的更深层次的现实。但是，有些时候，这种扩展是不可能的，甚至可以被证明是不可能的。这是因为函数只限于它最初的小定义域。这是一个非常广泛且深入的主题，我既没有足够的知识，也没有足够的时间来阐述它的最一般形式。

我想分享的是，实际上已经有工具来预测某种现象肯定不能超越其原始定义域的例子，它和无穷级数以及一个叫做解析延拓（analytic continuation）的概念有关。

延拓一个几何级数

看一下这个无穷级数

这是一个几何级数（geometric series），任何两个连续的项都有相同的比例，本例中的比例为1/2，这个级数的和恰好是2。

可以将这个概念推广到任何比例x，

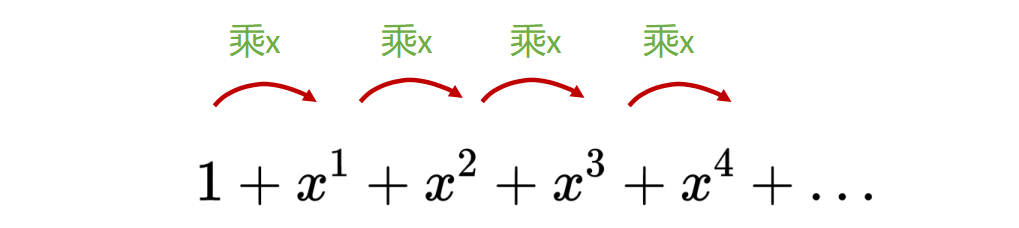
当x是介于-1和1之间的数字时，这个级数收敛，其和是，

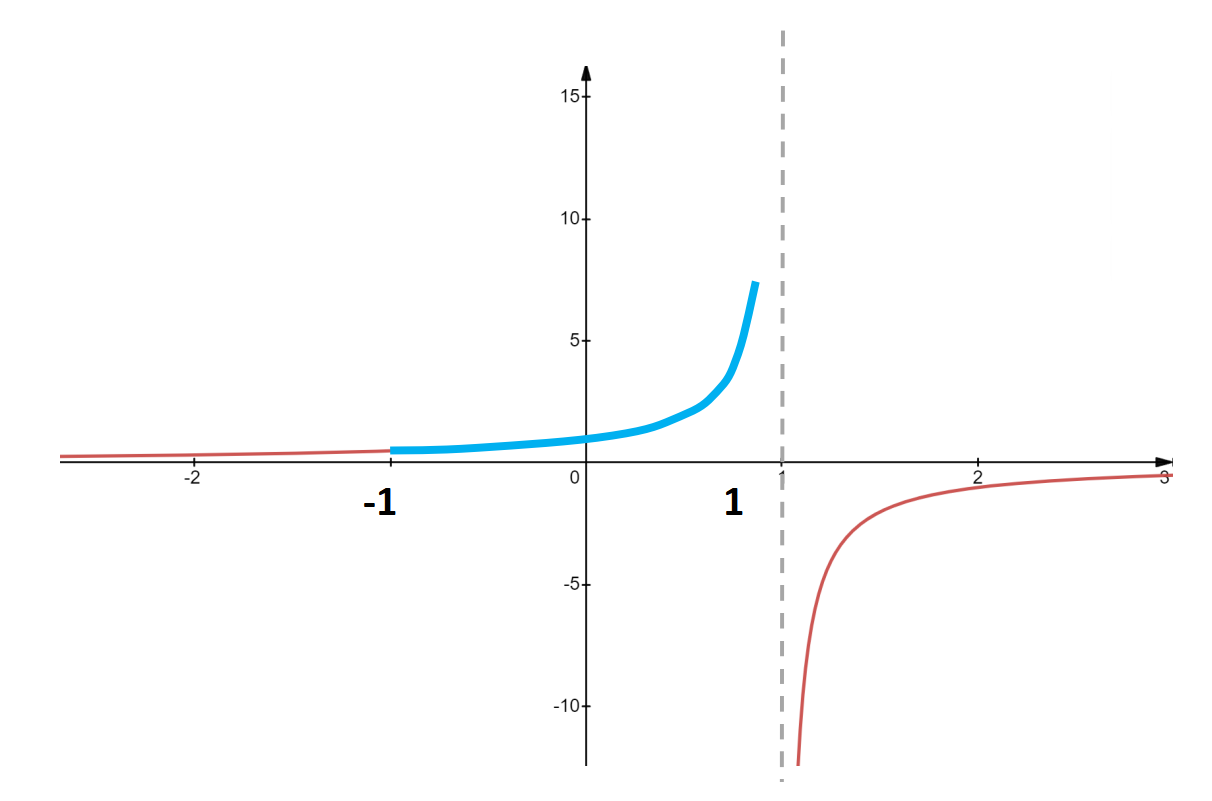
例如，当x = 1/2时，结果为2。但奇怪的是，即使在原始级数发散的x值上，这个公式仍然有效。例如，当x = 2时，级数变为，

所有2的幂的和显然是发散到无穷大的。但是用求和公式计算出来的结果却是-1。所以，尽管级数本身在-1到1的区间外没有定义，但我们找到的计算它的公式却可以（有定义）。这个公式成功地扩展了由级数定义的函数。

但是，现在让我们稍微改变一下这个级数，从中删除一些项，删除所有次数不是2的幂的项，留下来的是更稀疏的级数，

这个新级数实际上在相同的区间-1到1上收敛，

但是，原始级数可以被延拓到区间-1到1之外，这个新的级数，实际上不能被扩展。无论你怎么尝试，你都找不到一个能够将这个函数扩展到-1到1之外的公式，

从原始级数中删除一些项，使它不能再被扩展。但为什么呢？为了找到答案，我们将需要深入研究复平面。

复幂级数

下面的这种级数被称为幂级数（Power Series），

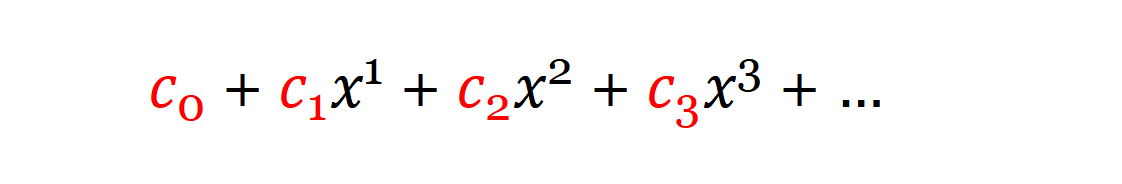
因为它们是x的无穷多个次幂的和。你可以将它们想象为一种无限次的多项式。如果你学过微积分，你可能知道它们的一些特性：比如它们总是收敛在一个有界的区间或者整个实数线上。这就引出了“收敛半径（Radius of convergence）"的概念，即收敛区间的中心到边界的距离，总是等于区间长度的一半。收敛半径完全受幂级数的系数的控制。改变系数，就改变了收敛半径。例如，所有系数都是1的幂级数，如经典的几何幂级数，

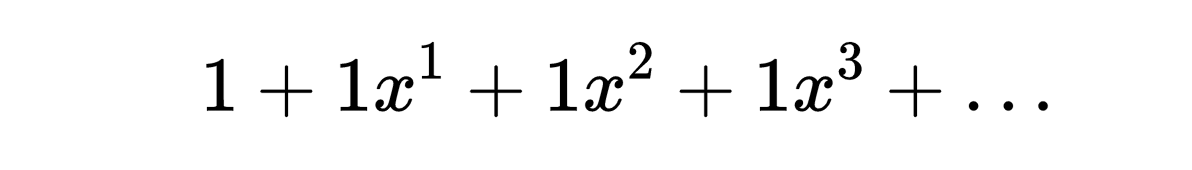
它的收敛半径是1。但是将系数改变为：

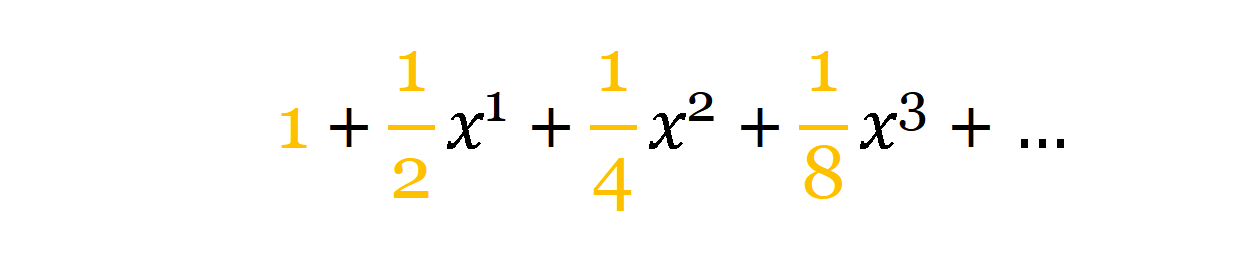
现在它的收敛半径就变为2，再次改变系数，

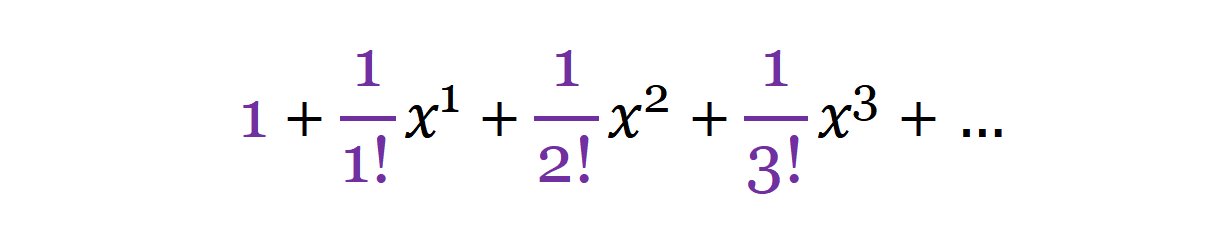
现在的收敛半径变为无穷大，它在整个实数线上收敛。

你可能会奇怪为什么要强调一个“半径”的收敛，为什么不直接谈论区间的长度，而要把它减半呢？其实，一旦进入复平面，这就会更有意义。

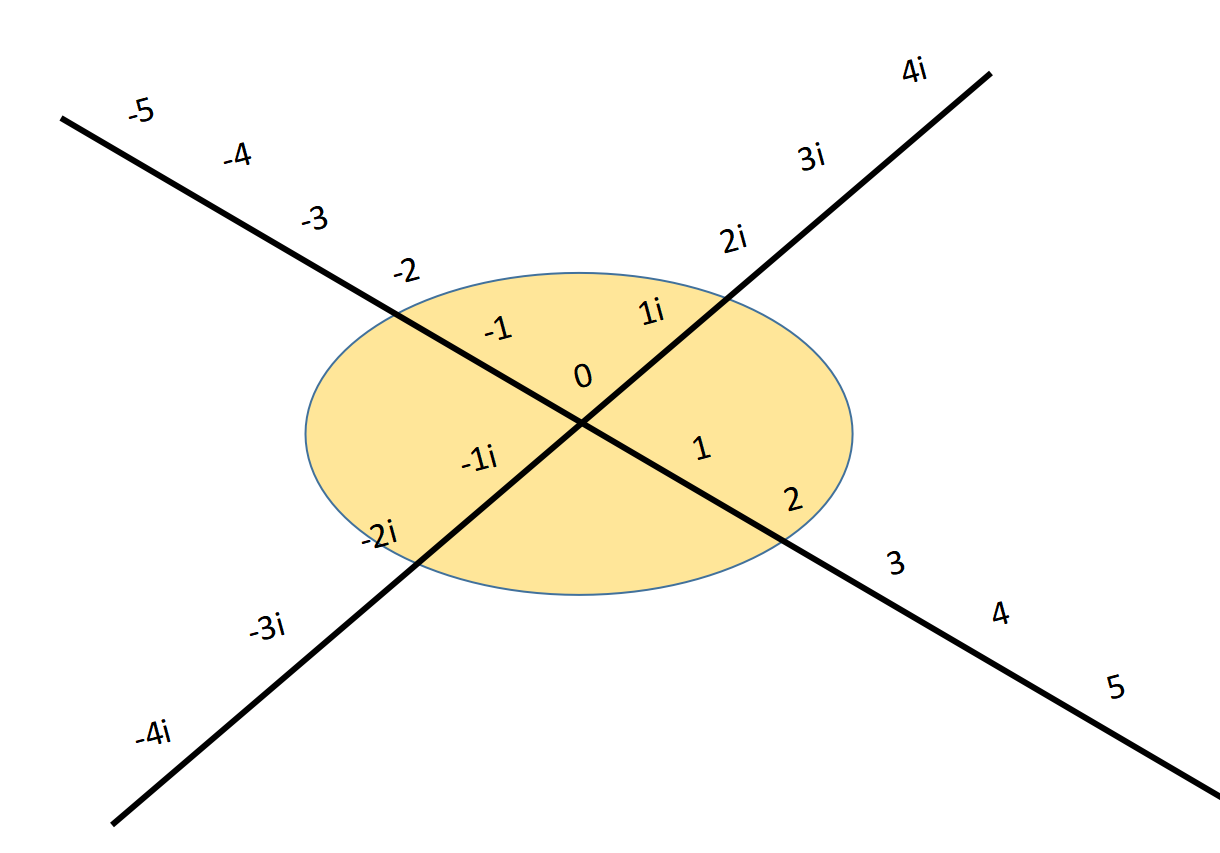
当允许幂级数中的变量x取复数值时，幂级数收敛的值在复平面上形成一个二维区域。就幂级数来说，这个区域总是具有圆盘的形状。例如，经典的x的幂级数，其中的系数都是1，在复平面上收敛在以原点0为中心，半径为1的圆盘内。

一旦处理复数变量，通常会使用变量z代替x，以此提醒我们它是复数。所以，现在开始，后面的复数变量用z表示。

实数函数1/(1-x)扩展了x幂级数的定义域。同样，复数函数1/(1-z)扩展了复数z的幂级数，把它扩展到了除了点z=1（因为这导致了“1除以0”）之外的整个复平面。

解析延拓

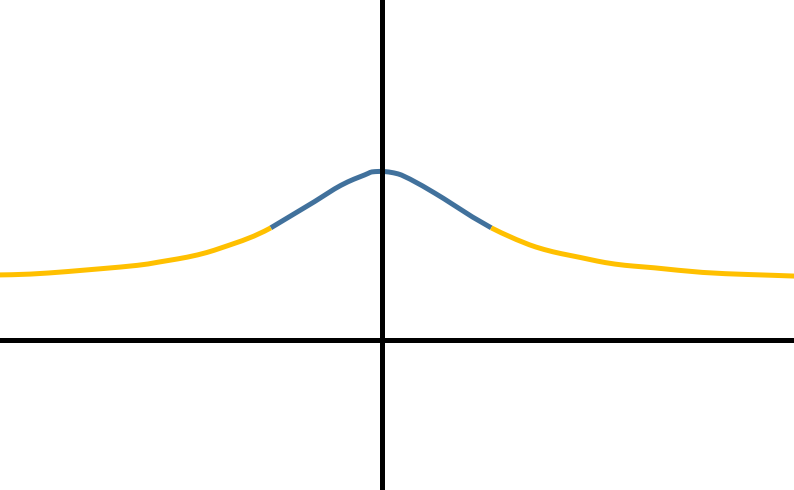
在继续之前，有必要明确这里所说的“扩展”函数的确切含义。给定任何图形，

你总是可以通过在其端部增加任何你想要的曲线来扩展它，

但是我们在这里所指的是一种非常特定类型的扩展。即，扩展需要在扩展域的每个地方，包括与原始域接合处的边界，都有一个导数。更重要的是，这个导数需要适用于复数。

这里无法详细解释复数导数是什么，以及它与普通导数有什么不同，但这对于本文来说无关紧要，你可以把它看作是一个更强的导数概念，它扩展了实数，但对函数的行为有更严格的约束。

此外，如果函数在其域的每一个点的邻域内都有一个复数导数，那么它是“行为良好的”，被称为“解析”函数，

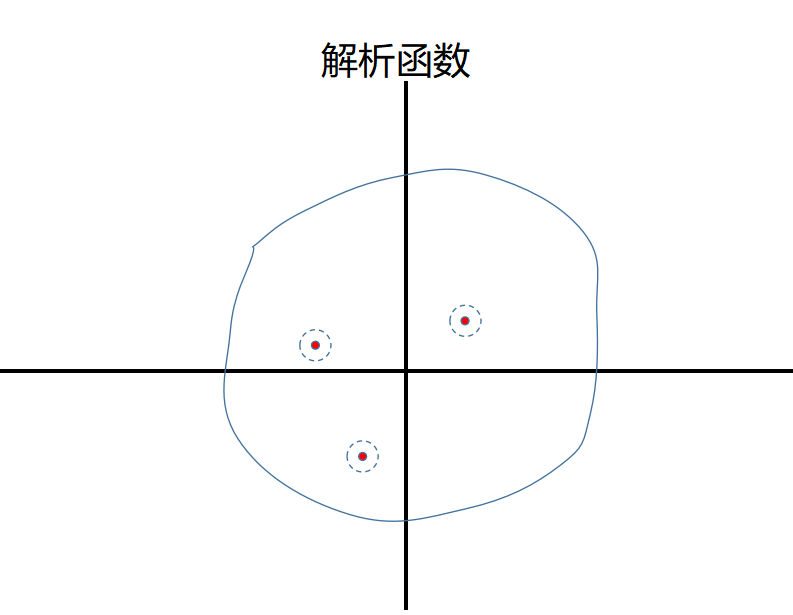
你见过的大部分函数都是解析的，如多项式、三角函数和指数函数。

所以大致来说，我们需要一个函数是解析的，以便用正常的公式来描述它。所以，如果我们想要扩展一个函数超越其原始定义域，并希望它会行为良好并可能有一个正常的公式，这就需要一个解析的扩展，学术称为称为“解析延拓”。

解析延拓是复分析中的一个基本概念。它涉及到将一个解析函数（即在其定义域内可导的复函数）从其原始定义域扩展到更大的定义域，同时保持函数的解析性。

解析函数：解析函数是一种在其定义域内任意点均可微（并因此无限次可微）的函数。这种函数通常可以用泰勒级数在其定义域内表示。

定义域延拓：如果一个函数在其原始定义域内是解析的，并且能在更大的区域内找到另一个解析函数与其相匹配（在两者的交集内函数值和所有导数都相等），我们就说这个新函数是原函数的一个解析延拓。

回到幂级数，复数函数1/(1-z)是z幂级数的解析延拓，它几乎适用于整个复平面——它在扩展域的任何点以及任何点的邻域内都有一个复数导数。

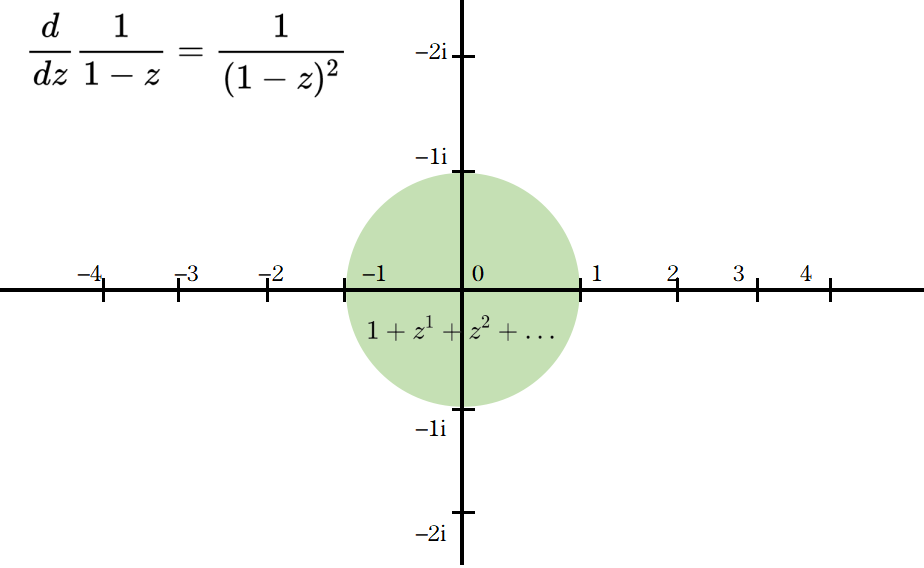
但是，按照某些规律删除一部分项后，比如只留下幂为2的幂的项，

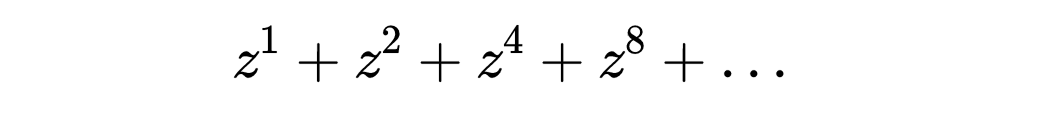
这个级数没有任何解析延续。但是，为什么？

分析间隔级数（Analyzing the Gap Series）

我们将频繁地将这个级数与原始的z的幂级数进行比较，其称为“间隔级数（Gap series）”，用函数g(z)表示它，并相应地用f(z)表示原始的z的幂级数。

首先，让我们试图可视化这两个级数，以便更好地理解间隔级数与原始级数的区别。

复数函数不能像实数函数那样被轻易地绘制，因为它们的输入和输出都是二维的，这意味着需要一个四维空间来以传统的方式绘制图形（这显然不可能）。但我们可以做的是将输入域中的一些点转换为相应的输出点。

在单位圆盘的中间放下一个极坐标网格，然后将f和g应用到网格中的每一点，

先从f开始，这是原始的良好级数。

单位圆盘在展开后覆盖了大约半个复数平面，你可以看到图案贴着这个黄色的垂直线，这就是这个函数的解析延拓开始的地方。

让我们看看间隔级数的情况如何？

网格似乎“爆炸”成一张混乱的网线。现在，我们不再尝试转换整个单位圆盘，而只转换一小部分，比如说，半径为1/2的圆盘，

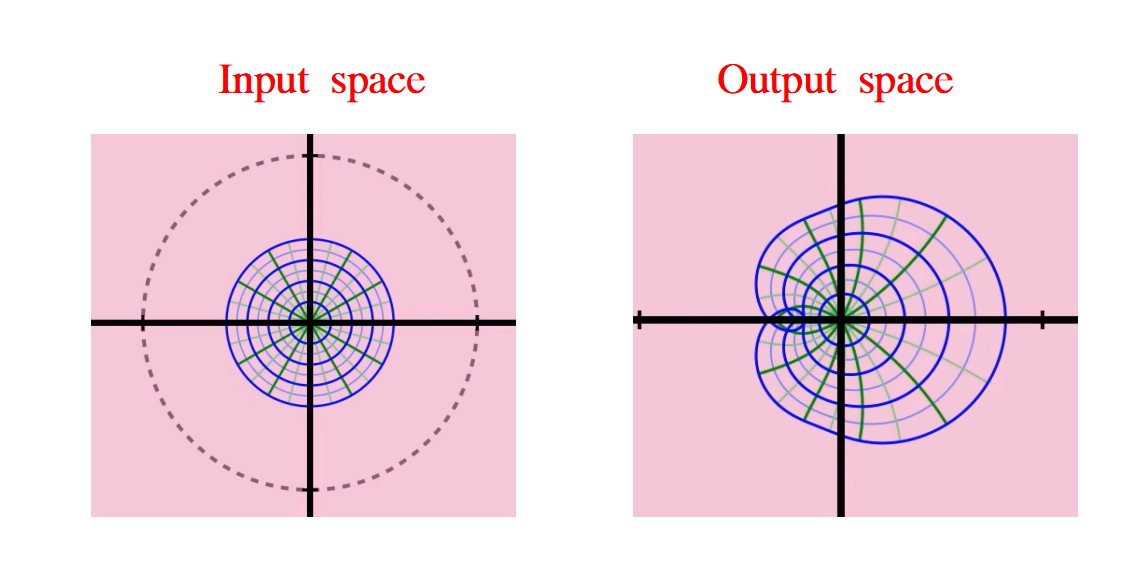
变换更为温和了。现在让我们看看当逐渐增加输入圆盘的半径接近1时会发生什么，

看起来越接近边界，变换就越疯狂。

如果在输入空间开始只画一个小圆，然后逐渐扩大会发生什么，

是的，问题就在这里。实际上，似乎选择输入圆的哪一部分都没关系。

如果将输入圆限制为只含有一个小圆弧，那么在间隔级数变换下，其g映像无论如何都会成为一个“爆炸的混乱”，

因此，看起来所有的混乱都发生在单位圆的边界上，这是有道理的，因为这是该级数从收敛转变为发散的地方。

这与原始级数f(z)形成对比，即使到达单位圆的边界，f(z)也表现得很好。它的映像接近成为一个垂直线，

因此，某种程度上，从这个级数中删除一些项，导致它在靠近外部边缘的输入处无法控制地增长。但是为什么呢？

可视化间隔级数

首先通过箭头链来可视化两个级数的各个项。从原始的z的幂级数f(z)开始。

这个蓝点表示输入到f级数的z值，用一串箭头表示f的项，每个箭头代表级数的一个复数项。

现在，显然我无法在屏幕上渲染无穷多的箭头，所以对于这个动画，我将其限制在大约25个箭头，这足够揭示问题的本质。

当z放在原点0时，只有一个箭头可见，这是代表常数项1的不变箭头，但当移动z时，开始看到其他项的贡献。

得到了一种螺旋形的箭头链，其中每个箭头之间的角度差总是相同，但每个后续的箭头都比前一个箭头短。这反映了一个事实，那就是连续地将一个点乘以一个复数z会使它按照z与正实轴的角度进行旋转。

所以例如，这个箭头，代表z的四次幂，

是原始z角度的四次连续旋转。箭头越来越短是因为z的更高幂有更小的大小，因为原始z的大小小于1。

要理解为什么原始f级数在接近边界时表现得如此良好，请看看它在输入点z接近单位圆上的某个特殊复数w时的行为，其中w是方程w^8 = 1的解。其中一个解就是1本身，但这里讨论的是复数平面，所以这个方程实际上有8个不同的解，它们均匀分布在单位圆上。

这些点被称为“八次单位根（8th roots of unity）”，因为它们中的任何一个的8次方都是1。

对于这个例子，将w选在这个位置，

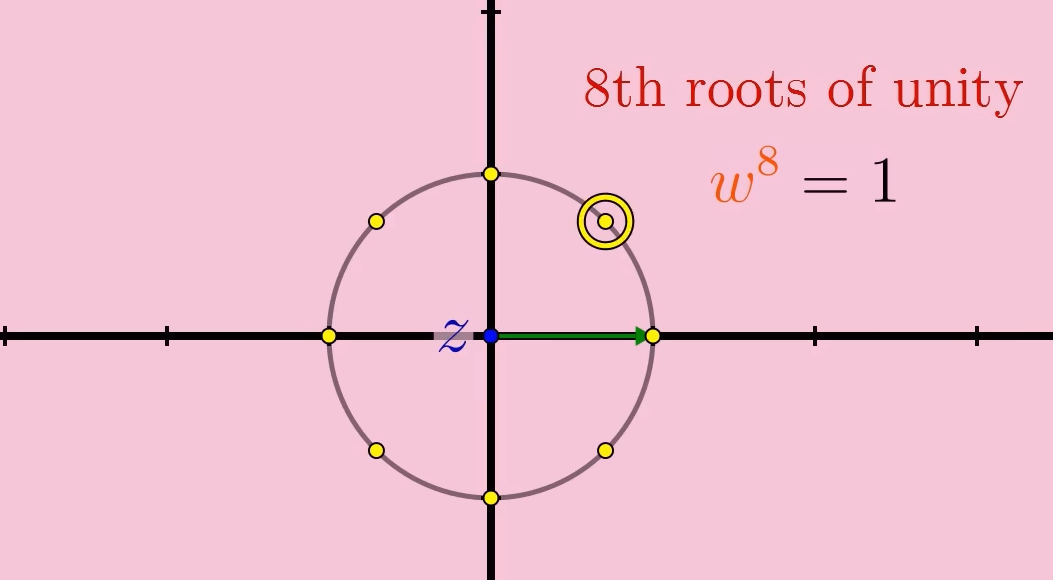
当我们将输入点z从原点向w延伸时，箭头链因为箭头收缩得更慢而更慢地螺旋向内，直到最后，当它达到w时，箭头不再收缩，变成一个多边形的箭头链，永远在一个周期内旋转。

实际上，它形成了一个正八边形，这是有道理的，因为它是一个8次单位根。

当然，这是一个发散的级数，因为箭头只是在一个周期内绕圈，没有接近任何东西，但至少它没有发散到无穷大！

实际上，如果将输入点稍微移离w，箭头链现在会螺旋向一个八边形的中心，即使它是非常慢的。

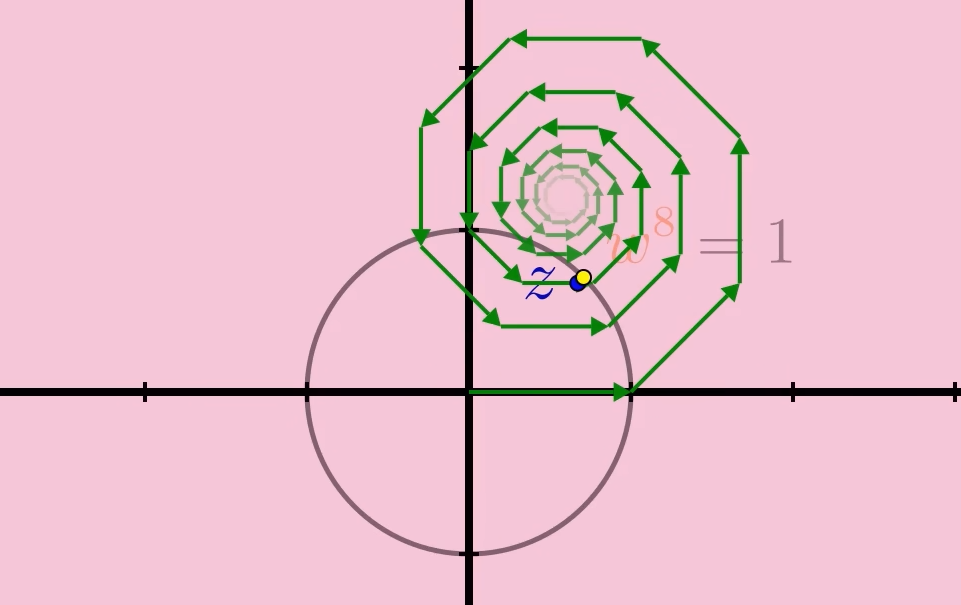
所以即使在w处级数是发散的，它似乎想成为它形成的八边形周期的中心，这给了我们一种将级数扩展到w的方法。

让我们看看间隔级数g。相同的设置：从原点开始我们的输入点，然后逐渐将它滑向w。

这很奇怪，箭头链最终变成了一个直线链，朝着右边前进。为什么会这样呢？

注意，链中的每个箭头都代表级数中的一个不同项。在这种情况下，其项是z、z^2、z^4、z^8等等。级数中的每一项都是前一项的平方：z^4是z^2的平方，z^8是z^4的平方。对于复数，将它们平方会导致它们与正实轴形成的角度翻倍。例如，复数i与正实轴形成90度的角度，所以将它平方就会将该角度翻倍至180度，将其放在数字-1上。

在这种情况下，当z接近w，如果足够多次对w进行平方，最终将得到w^8，之后就会停在1，1的平方仍然是1。

从某种意义上说，由于间隔级数只包含z的2的幂的项，因此当z接近1的8次方根时，它们之间有一种“Constructively interfere”，而原来的z的幂级数f(z)的项有一种“Destructively interfere”，以收敛到一个稳定的值。对于1的16次和32次方根等等，这种"现象也会发生！实际上，间隔系列g(z)将会在z接近任何1的2的幂次方根时发散！

所有1的2的幂次方根的集合形成了单位圆的一个密集子集，

这意味着单位圆上的每一个点要么本身就是1的2的幂次方根，要么是无限接近一个，就像每个实数要么是有理数，要么无限接近一个无理数一样。所以，单位圆包含了使间隔级数g(z)向无穷大发散的“奇点森林”。然而，并非单位圆上的每个点都是这些寄点。实际上，大多数并不是。那么，或许我们还是有可能通过某种方式在奇点森林之间将g解析地继续下去？

然而，在这里遇到了一个致命的问题。记住，解析函数是在其定义域的每一点以及每一点的局部邻域内都有复数导数的函数。所以，要将g解析地延续到单位圆上的一个点，至少需要在它周围有一个局部区域，无论多么小，在那里g能保持有界。但是，无论这样的区域有多么小，它都会包含一些使g发散的寄点。因此，间隔级数被无限奇点的森林困住。

间隔定理

这就完成了对这个特定间隔级数的证明，但你可能还想知道哪些其他幂级数，或更一般的复函数，不能被延拓超出它们的初始定义域。这是个很大话题，但有几个定理可以进一步将我们得到的结果推广到其他在z的幂之间有“间隔”的幂级数。

第一个也是最简单的被称为Hadamard间隔定理，它说如果一个幂级数在z的幂之间有间隔，并且这些间隔至少以几何序列的速度增长，那么它不能被解析地延拓超过其收敛盘。这告诉我们关键是间隔增长的速度，而不是它是否精确地遵循某种模式。

然而，事实证明，这个定理实际上可以被大大地强化。间隔实际上不必像几何级数那样快速增长；只需要它们增长得比所有线性级数更快就足够了。所以例如，间隔可以增长得像

那样慢，这一事实被称为Fabry间隔定理。

从某种意义上说，这大约是你能希望得到的最强的“间隔”定理，因为另一个结果，被称为Pólya定理，告诉我们，如果间隔增长得比某个线性级数更慢，那么就可以选择一些序列的系数，使得它可以在它的收敛盘之外被延拓。

文章来源：Morphocular的视频：“When CAN'T Math Be Generalized? | The Limits of Analytic Continuation”