
在过去的两年中,数学家们专注于发现各种简单形状的最理想表现形式,探索在特定限制条件下能最有效实现既定目标的形状,即“最优”形状。这个概念涉及在给定的约束(如空间大小或材料限制)下,找出最具效益或效率的几何形状。自然界中蜜蜂建造的六角形蜂巢是一个典型例子,展示了这一原理。蜜蜂本能地选择六边形结构来构建蜂巢,因为这种形状在占用最小空间的同时能提供最大的存储容量,这正是在资源有限的情况下选择最佳形状的实际应用。
布朗大学的理查德·施瓦茨教授和他的研究团队,包括他的妻子布丽安妮·伊丽莎白·布朗,一直在探究最优形状领域的问题。施瓦茨教授指出,他们的研究集中于一系列对象,旨在确定哪些形状能在特定条件下实现某些属性或功能的最大化或最小化。自上年八月以来,他已经发布了三项这方面的重要研究成果。
这些研究主要关注如何使用最少的材料,例如纸张、绳子或绳索,来构造特定的形状。其中一个关键的成果涉及莫比乌斯带(Möbius strip),这是一种通过将纸条扭曲一次并连接两端而形成的特殊几何形状。莫比乌斯带的独特之处在于它只有一个表面,这意味着可以在笔不离开带子的情况下沿着它的表面绘制一圈。施瓦茨教授的工作不仅揭示了这些形状的独特几何和拓扑特性,而且还展示了如何以最经济的方式构造这些形状,对于理解材料利用效率和形状的本质特性具有重要意义。

从20世纪30年代开始,数学家们就在探索能够制作成莫比乌斯带的矩形的最小尺寸。关键的问题是确定矩形的最短长度,以便在扭曲后仍能将两端连接起来形成莫比乌斯带。实际上,将一个长条形状的矩形扭曲成莫比乌斯带相对容易,因为它的长度足以在扭曲后连接两端。相反,将一个正方形(长度和宽度相同)转化为莫比乌斯带则似乎是不可能的,因为它的长度不足以允许扭曲后的连接。因此,数学家们试图找出长和宽之间的最优比例,这样的矩形既能够被扭曲成莫比乌斯带,又是尺寸上的最小可能(即临界点)。
在探讨最优形状时,数学家通常会关注最小化或最大化特定数值,例如条带的宽度与长度的比例。这一过程涉及寻找一种形状的极端表现,即在特定条件下形状的理想或高效表现形式。
最优形状的研究构建了几何学与拓扑学之间的联系。几何学关注具体的量度,如长度和大小,而拓扑学则专注于那些理想化的对象,这些对象在理论上可以无限伸展或压缩。在拓扑学的视角中,尺寸和形状的不同并不影响对象的基本性质。例如,莫比乌斯带在拓扑学中被视为相互等效,因为大小不同的莫比乌斯带可以通过伸展或压缩转换。这意味着,无论其实际尺寸如何,所有矩形条带在拓扑上被认为是相同的。

当一条带子经过扭曲并将两端相连形成莫比乌斯带时,这种操作实际上在挑战拓扑学的边界。莫比乌斯带的制造过程涉及改变带子的基本拓扑结构,从而创造出一个全新的形状,具有唯一连续的表面。
在研究最优形状时,特别是处理像莫比乌斯带这样的结构,本质上是在探索拓扑学的极限。拓扑学关注的是物体在经历连续变形(例如伸展或压缩)时保持不变的属性。因此,对于莫比乌斯带来说,关键问题是它能被挤压或拉伸到何种程度,而仍然保持其作为莫比乌斯带的拓扑特性?
近年来,在最优形状的研究领域,已经有至少五项重大发现,它们为不同的几何形状确定了新的最佳值。这些形状包括莫比乌斯带、三扭莫比乌斯带(three-twist Möbius strip)和简单结(simple knot)。一部分研究确立了这些形状的最佳值,这些值可能涉及到在特定条件下的最高效率或最低材料消耗。另外一些研究则证明了对于这些形状而言,已发现的最佳值是目前能够达到的极限,暗示着在当前的技术和理论水平下,不可能有更优的值。
最优莫比乌斯带
数学家们采用了被称为纵横比的数值来衡量矩形有多接近于一个正方形。纵横比是通过将矩形的长度除以其宽度来计算的。在这种计算方式下,一个正方形的纵横比是1,因为它的长度和宽度相等。另一方面,一个长条形状的矩形,像丝带一样,由于长度大大超过宽度,它的纵横比会更高。
这个概念在将矩形材料扭曲成特定结构时尤为重要,比如在制作莫比乌斯带时。具有较高纵横比的矩形,由于长度充足,可以较容易地被扭曲并连接成一个环状结构。然而,随着矩形的尺寸变短,其纵横比趋向于1,也就是越来越接近正方形的形状,进行这样的扭曲变得越来越难。一旦矩形足够短,几乎成为一个正方形,它可能就无法被有效地扭曲并连接成所需的结构了。因此,纵横比是判断矩形材料在制作特定几何结构时的可行性的一个关键因素。
1977年,两位数学家猜想,要使固定宽度为1的矩形能够扭曲成莫比乌斯带,它的长度必须超过√3。

2023年8月,施瓦茨证明了他们是正确的。
你可能会想找一个巧妙的解决办法。通过将正方形纸张像手风琴一样折叠成一条纸带,然后将其扭曲。这种方法似乎巧妙地解决了如何从一个较大的纸张中得到足够长的纸带的问题。但这种手风琴式的折叠方式在折痕处产生尖锐的角,而不是数学上所指的平滑曲线或表面。在数学用语中,“平滑”通常描述的是无断点、连续且没有尖锐转折的曲线或表面。因此,尽管这种折叠的正方形可以在物理形态上被扭曲成莫比乌斯带,但由于其折痕的尖锐角度,它不符合数学上定义的莫比乌斯带的平滑特性。
在确定最优形状的特征时,使用了一种称为“极限形状(limiting shape)”的关键概念作为工具。极限形状在某些重要方面与原始的优化对象不同,但同时也保持了一些共同的特征。举个例子,如果不断地拉长一个矩形,它会逐渐变得更细,最终看起来像一条线。同样,随着多边形边数的增加,其形状越来越接近于一个圆。在这两种情况中,矩形和多边形的极限形状分别变成了线和圆。这些极限形状虽然在某些属性上与原形状有所不同,但仍然保留了一些基本的几何特性。通过研究极限形状,可以获得关于形状的最优特性和可能性的深入见解。
在这种情况下,施瓦茨为莫比乌斯带创建了一个极限形状。从一块宽1单位、长√3单位的矩形纸开始。按照以下方式进行折叠,

开始时,你需要把纸张从左上角向下折,然后从右下角向上折,这样操作会使纸张变成菱形状。紧接着,在菱形的中线处折叠,并使用胶带把在菱形内相交的边(这些边在上图1中以蓝色和黄色虚线表示)粘合在一起。之后,通过调整纸带的长度或宽度来给予结构一些弹性,使得可以展开折叠形成的三角形。这样操作后得到的结构就是一个莫比乌斯带。在这个莫比乌斯带上,一个无穷小的蚂蚁如果在三角形表面上沿着折痕行走,就会绕行一圈——它只有一面。
数学家们早已知道,这样的三角形是莫比乌斯带的极限形状。施瓦茨证明了其他可能让条带更短的极限形状并不存在。为了证明这一点,他特别使用了由三角形折痕构成的“T”形,如上面最右边的三角形所示。
施瓦茨在他的研究中巧妙地将拓扑学和几何学的理念相结合。在拓扑学领域,他表明在莫比乌斯带的每一片纸上都能画出一种特殊的相交线条,这些线条组合起来形成一个"T"形。这一点在拓扑学中是有意义的,因为拓扑学关注的是物体在不断变形时保持不变的性质。
继而,他利用几何学的基本原理,特别是毕达哥拉斯定理和三角不等式,来证明这样的"T"形必然意味着原始纸带的长宽比必须超过√3。这个发现意味着为了构造一个莫比乌斯带,条带的长度必须至少是宽度的√3倍。
最优扭曲圆筒
在施瓦茨确定了最优莫比乌斯带之后,很多人自然会问到:如果增加扭曲次数会怎样?任何奇数次的扭曲都会产生一个莫比乌斯带,因为结果形状仍然只有一面。另一方面,偶数次的扭曲产生一个叫做扭曲圆筒(twisted cylinder)的双面结构(如下图左侧所示)。不同于普通的圆筒,它没有明确的内外之分。
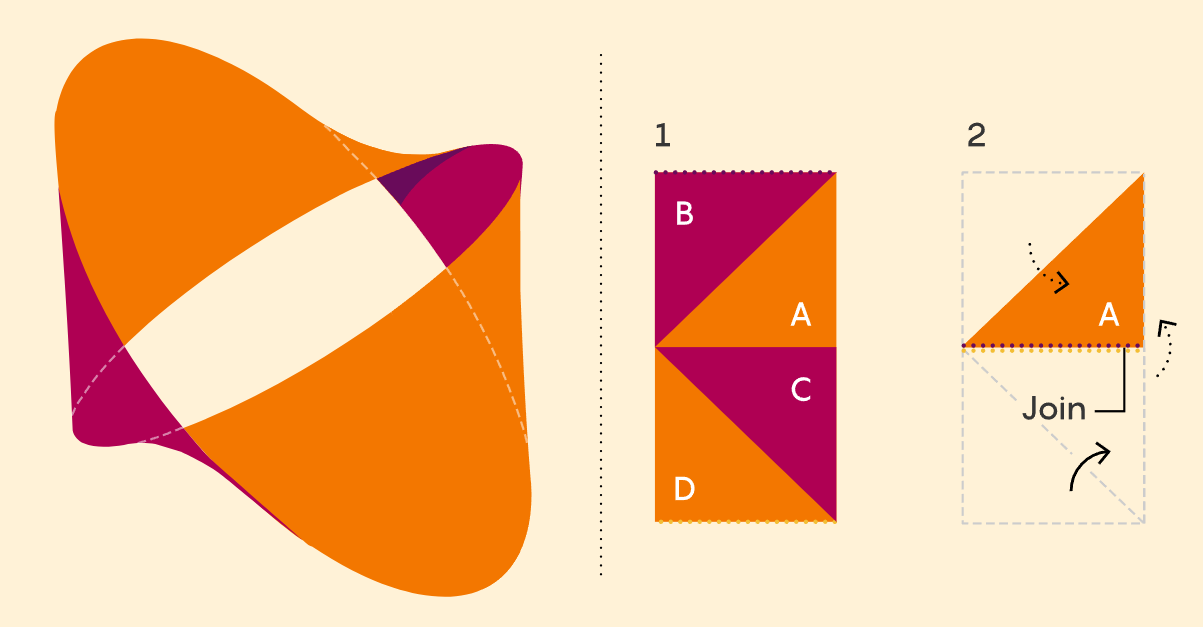
在完成了关于莫比乌斯带的论文之后,施瓦茨在9月下旬证明了扭曲圆筒的极限形状可以通过折叠一个1×2的矩形制成,该矩形由四个堆叠的直角等腰三角形组成(如上图右侧所示)。首先,将B三角形折叠到A三角形后面,将D三角形折叠到C三角形上面(虚线箭头表示向后折叠,实线箭头表示向前折叠)。然后将得到的三角形对折,将下半部分折叠到上半部分后面。接着将蓝色和黄色的虚线(原本是矩形的上下部分)用胶带粘在一起。最后,使起始的矩形稍微变长一些,以便有足够的松弛度将扁平的形状拉伸成一个挤压的扭曲圆筒。
基本的想法是先构建极限形状,然后稍微放松一些并圆滑折痕,施瓦茨写道。
如图所示(上图右侧),堆叠的三角形形状的长度是其宽度的两倍,因此扭曲圆筒的最优纵横比为2。
最优三扭莫比乌斯带
施瓦茨接下来的研究专注于具有三次扭曲的莫比乌斯带,这是一个仍然保持单面特性的形状,但由于增加了两次扭曲,其边界结构比单次扭曲的莫比乌斯带更复杂。这种三扭莫比乌斯带被认为可能对应于一种称为六边形变形体的极限形状,这是一种由等边三角形组成的几何结构。这种结构具有通过挤压边缘来改变其形状的能力,这种变形方式类似于某些游戏中的操作,使得不同的三角形部分显露出来。
但施瓦茨的妻子布丽安妮·伊丽莎白·布朗开始自己用纸玩耍,质疑了六边形变形体作为三扭莫比乌斯带极限形状的假设。布朗找到了一个她称为“交叉”的构造(如下图所示),

这是三扭莫比乌斯带的极限形状,其长度是宽度的三倍。首先沿着条带中间的对角线折叠,将下部分放到上部分的前面。然后将右上方的三角形折叠到其左下方的三角形的前面。现在你得到了步骤2中的形状:一个倾斜的平行四边形,右侧突出一个正方形。将正方形放到平行四边形后面,将顶部的三角形放到现在在其下方的正方形前面。这样制成了步骤3中显示的新正方形。
最初的顶部和底部边缘(由蓝色和黄色虚线显示)现在都在正方形的左侧边缘;将它们粘在一起,就创造了一个三扭莫比乌斯带的极限形状。就像一扭带的情况一样,这个平面形状本身不是莫比乌斯带,但如果给它稍微增加一点长度,使其能够在三维空间中松弛开并且没有尖锐的弯曲,它将形成一个三扭带。
最佳三叶结
在最优形状的研究中,数学家们的兴趣并不仅局限于莫比乌斯带的各种变体。他们还在探索制作各种不同类型的结需要多少材料。例如,在2020年,两位本科学生专注于研究那些能够在圆环面上(一种类似于甜甜圈的形状)画出来的结。
在这些结中,最简单但非常规的一种被称为三叶结。这种结的形成类似于系鞋带时的一个常见步骤:使用一根绳子或鞋带形成一个圈,然后将一端穿过这个圈。然而,与完成系鞋带的蝴蝶结不同,三叶结是通过将鞋带的两端直接粘合在一起形成的,最终形成一个平结,两端呈松散状态。通过这样的研究,数学家们可以更好地理解在特定的几何形状上构造这种结所需的最优材料量。
通常系三叶结的方式等同于用一根绳子绕在圆环面上,如此处所示:
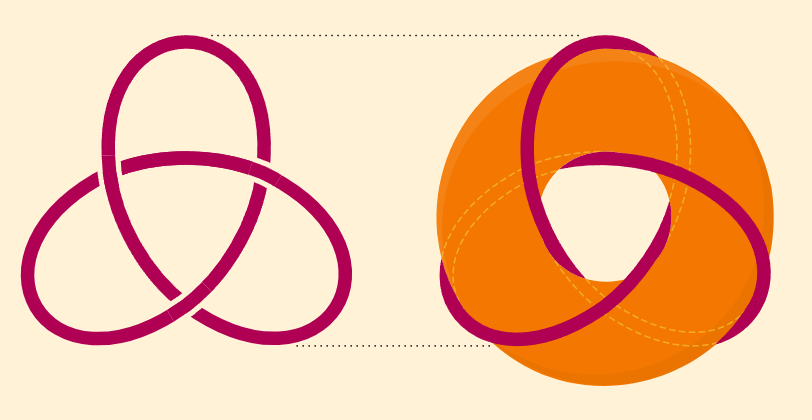
这种结在数学上可以被一条无限细的线定义。同样,这种结也能适用于丝带,正如在莫比乌斯带的情况中看到的那样,其中丝带被看作是一种理想化的纸条。就像使用极细的线一样,你也可以用丝带来打这种结,如下所见,

如果你将丝带拉紧并压平,这种缠结会产生一个五边形的极限形状。
然而,这并不是将丝带打成三叶结的最佳方式。Denne和她的学生们找到了更优的方法。他们的一种方法从三条平行的条带开始,每条条带的长度是其宽度的两倍。他们找到了一种将条带折叠并连接两端的方式,以形成具有不同极限形状的三叶结。这种方法以及他们用丝带打三叶结的另一种新方式都产生了6的长度与宽度比,超越了之前已知的最佳比例6.882。
用三维的绳索替换二维的丝带。形成一个三叶结需要多长的绳索?在2006年的研究中,Denne、Yuanan Diao和John Sullivan发现,要构成一个三叶结,至少需要一根直径为1单位的绳子,长度达到15.66单位。这个长度也被认为是打任何类型结所需的最短长度。数值模拟的结果表明,可能使用的最长绳子长度不超过16.372单位。尽管如此,关于这个问题的确切答案仍然未知,只能确定它位于这两个数值之间。
现代数学的许多领域对于非专业人士来说可能显得过于抽象,与日常生活的联系也不明显,但最优形状的研究却是切实可行且具体的。例如,最优的三叶结之类的丝带结被用于模拟分子生物学中的DNA结构,这不仅有助于解决具体问题,还为探索结理论领域中更抽象的问题提供了一个起点。通过简单地操作纸张,人们能够轻松入门并对数学进行深入的思考和理解。
