什么是数论?人们可能这样想过：数论只不过就是对于数的研究，但是这样的定义过于空了，因为数在数学里几乎是无处不在的。要想看清是什么把数论和数学的其他部分区别开来，我们来看一看方程，并且考虑它是否有解，

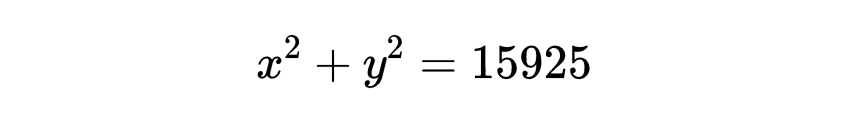
一个答案可能是：它确实有解。事实上，它的解集合是平面上的一个半径为√15925的圆周，

然而，数论专家感兴趣的是它的整数解，而这个方程是否有整数解存在就远不是那么显然的事情了。

考虑这个问题的有用的第一步是看到15925是25的倍数。15925=25×637。进一步，637又可以分解为49×13，那么15925=52×72×13。这个信息对我们很有帮助，因为如果能够找到整数a和b，使得a²+b²=13，就可以用5×7=35去乘整数a和b，而得到原方程的整数解。现在我们注意到a=2，b=3。把这两个数乘以35，就得到原方程的整数解x=70，y=105。

这个简单的例子说明，因式分解通常是有用的。这些不能再分解的“因子”就称为素数，而算术的基本定理指出，每一个正整数都恰好可以用一种方式分解为素数的乘积。就是说，在正整数和素数的有限乘积之间有一个一一对应。在许多情况下，只要我们知道了如何把一个正整数分解为素数的乘积，就知道了关于这个正整数很多东西。正如只要研究构成一个分子的原子，就能理解关于这个分子的许多东西。

例如我们知道，方程x²+y²=n有整数解当且仅当在n的素数因子中，每一个形如4m+3的素数都出现偶数次。这就告诉我们，例如x²+y²=13475就不会有整数解，因为13475=5^2×72×11，而11=4×2+3虽然也是4m+3形式的素数，却只出现一次。

一旦我们开始了确定哪些数是素数而哪些不是素数的研究，马上就会看出有许多素数，再顺着向更大的正整数走，又会发现，在正整数中，素数所占的比例越来越小。它们又是以一种不规则的模式出现的。

这就提出一些问题：

是否可以找到一个公式来描述所有素数？如果这一点不成功，那么，能不能描述很大一类素数？

还可以问，是否存在无穷多个素数？如果是，那么能否迅速地确定，到某个界限为止，多少素数？至少是给出素数数量的一个好的估计。

最后，当我们已经花了很大精力来寻求素数，就不能不问有没有快速的方法来识别出素数。

既已讨论了数论和数学其他部分的区别，我们就准备好了进一步区分代数数论与解析数论。主要的区别在于，在代数数论中，典型情况下，我们讨论的问题的答案都是由准确的公式给出的，而在解析数论中，我们寻找的是好的近似。在解析数论里所要估计的那一类量，一般都不能希望有准确的公式存在，除非愿意接受那些人为造作的没有启发性的公式。这一类量的最好的例子之一，就是我们将要详细讨论的：小于或等于x的素数的个数。

既然我们要讨论近似，就需要一些术语来使我们对于这种近似的程度有一点概念。例如设有某个相当不确定、不可靠的函数f(x)，但是我们能够确定，当x足够大时，它不会超过25x^2。这个信息已经是相当有用的，因为我们对函数g(x)=x^2有相当好的理解。一般说，如果能够找到一个常数c，使得对于每一个x都有

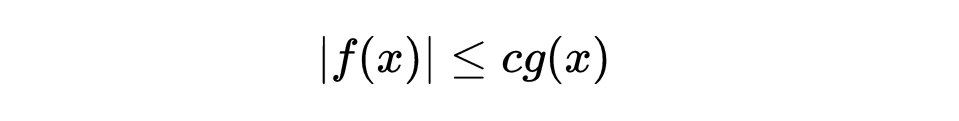
就写作

下面这句话就是这个记号的典型的用法：

到x为止的整数的素因子的个数的平均值是loglogx+O(1)。

换句话说，存在某个常数c使得当x充分大时，

如果lim f(x)/g(x)=1，就写作f(x)～g(x)；如果没有这么精确，就是说，如果我们想说的只是：当x充分大时f(x)和g(x)很接近，就写作f(x)≈g(x)，但是这里对于什么是“很接近”我们不能或者不想说得很确切。

用记号

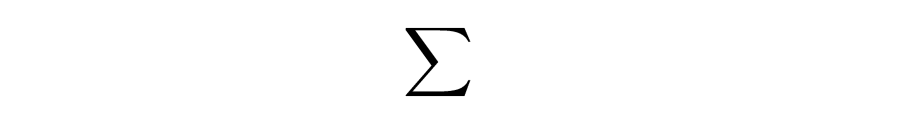
来代表和，用记号

来代表积，是很方便的。典型情况是在这些记号下方注明是求哪些项的和或哪些因子的积。例如，

表示对所有大于m≥2或等于2的正整数m求和，而

代表对所有素数p求乘积。

素数个数的界

古希腊数学家就已经知道素数有无穷多个。他们的漂亮的证法如下：假设只有有限多个素数，例如有k个，记作

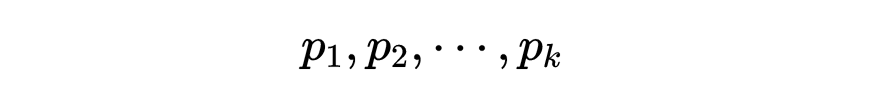
那么

有哪些素数因子？因为这个数比1大，所以一定至少有一个素数因子，而这个因子必须是某一个p_j（因为所有的素数都已经包含在p_1，p_2，…，p_k中了）。但是这样一来p_j就能够同时除尽p_1p_2…pk和p_1p_2…p_k+1，因此也应该能够除尽二者之差1，而这是不可能的。

到了18世纪，欧拉对于存在无穷多个素数给出了另一个证明，而这个证明对于后来的发展有很大的影响。再一次设素数可以列表如下：

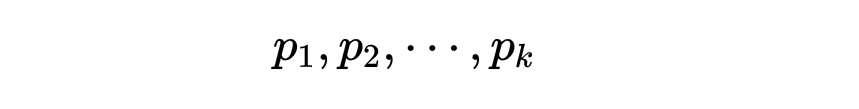
正如我们已经提到过的，算术的基本定理蕴含了所有整数的集合与素数的所有乘积的集合之间有一个一一对应，而后一个集合，如果上面给出的列表（p_1，p_2，…，p_k）就是全部素数的话，那么

可以生成所有大于1的自然数的唯一素数分解。

但是欧拉看到这就蕴含了第一个集合的元素之和应该等于第二个集合的元素相应的和：

以上等式不是很明显，如果你没有看出来不要沮丧，毕竟欧拉也是经过研究才得出的。

最后一个等号之所以成立，是因为倒数第二行的每一个和式都是一个几何数列的和。然后欧拉就注意到，若取s=1，则最后一式是一个有理数，而最前一式是无穷大。这是一个矛盾，所以不可能只有有限多个素数。

在上面的证明中，我们从素数个数为有限这个假设得出了这个公式

为了纠正这一点，需要我们做的仅只是用明显的方式而不用这个假设就能重新写出

式（1）

然而这时我们要小心一点，注意公式双方是否为收敛。当双方都是绝对收敛时，写出这个公式是安全的，而当s>1时，确实双方都是绝对收敛的（如果一个无穷和或无穷乘积是绝对收敛的，则任意改变各项或各个因子次序时，其值不变）。

我们也和欧拉一样，希望能够解释当s=1时，对(1)式会发生什么情况。因为当s>1时，(1)式双方都是收敛的而且相等，所以一件我们自然会做的事情就是考虑当s从大于1的方向趋向1时双方的公共极限。为此注意到，(1)式的左方可以用

来逼近，所以当s→1+时，它是发散的，由此可知

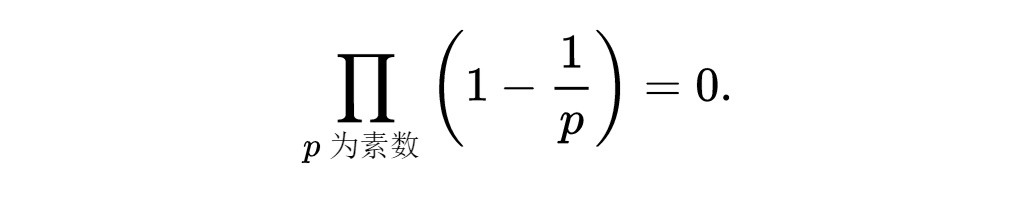
式(2)

取对数，并且略去可以略去的项，得到

式(3)

那么，素数到底多到什么程度？想要得到一点感觉的方法之一是考虑，对于其他整数序列，与(3)相类似的性态如何。例如

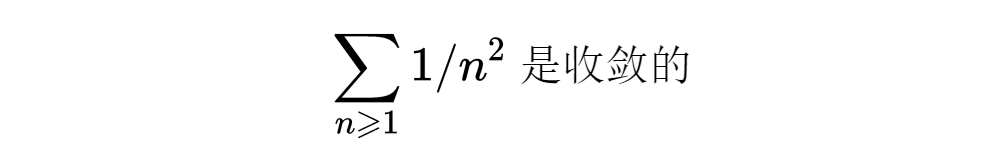
所以，素数在一定意义下，比完全平方数要多得多。如果把上面的指数2换成任意s>1，这个论据也是可以用的，因为我们已经看到

所以也是收敛的。事实上，因为

所以在同样的意义下，素数的集合比形如

的集合要大得多，所以有无穷多个整数x，使得小于或等于x的素数的数目至少是x/(logx)^2。

这样，素数确实是为数众多。但是我们也想用来自计算的一点观察来验证一下，即当整数变得越来越大时，则素数集合只构成整数集合的越来越小的部分。想要看到这一点，最容易的方法是利用所谓“埃拉托色尼筛法”。在埃拉托色尼筛法中，从1直到x的正整数的集合开始。从中删去4，6，8等等所有2的倍数，但保留2。然后取保留下来的最小的大于2的数，即3，然后从1直到x的正整数中删去所有它的倍数，而只保留3。然后删去所有5的倍数，但是保留5。仿此以往，就会得到直到x为止的所有素数。

这就提示了一种猜测究竟有多少素数的方法，就是每隔一个整数就删除第二个整数（但是保留2，这叫做“筛去2”），这样，在到x为止的整数，留下的只有一半左右；在筛去3以后，在上次余下的整数中，又只留下其三分之二。像这样做下去，在删去到y为止的素数以后，余下的整数的个数大体上应是

式（4）

一旦y=√x，则未被筛去的整数就只有1和到x为止的素数，因为在x前面的合数都含有不大于其平方根的素数因子。那么，当y=√x时，(4)式是否给出了到x为止的素数的个数的很好估计呢？

要回答这个问题，就需要弄清楚，(4)式估计的究竟是什么。设想它估计的是到x为止的一类整数的个数，这类整数没有小于或等于y的素数因子。如果用所谓的包括-排除原理（inclusion-exclusion principle）来证明，则可以得到(4)式的误差最大是2^k，这里k是小于或等于y的素数的个数。除非k很小，2^k这样大的误差项远远大于我们想要估计的量，所以这种近似是没有用处的。如果k小于一个很小的数乘以logx，这个误差又是很小的，但是，如果y≈√x的话，这样的k远小于我们所期望的直到y的素数的个数。这样，就不清楚是否可以用(4)式来得出直到x为止的素数个数的好的估计。

然而，我们能够做的是应用这样的论据来给出直到x为止的素数个数的上界，因为直到x为止的素数的个数绝不会多于直到x为止某一种整数的个数再加上直到y为止的素数个数，这就不超过2^k加上(4)中的表达式；上面提到的“某一种整数”就是没有小于或等于y的素数因子的整数。

由(2)式可知，当y变得越来越大时，

所以对任意小正数ε都可以找到一个y使得

因为这个乘积的每一个因子至少是1/2，所以乘积至少是1/2^k，于是对于x≥2^(2k)，误差项就不大于(4)中的量，而直到x为止的素数的个数就不大于(4)的两倍，而由y的选择，也就是小于εx。由于ε可以选得任意小，这就是说，素数所占的x的比例一定趋于零，而这正是我们预料中的情况。

虽然包括-排斥原理的误差太大，不能在y=√x时用这个方法用(4)式来作估计，但我们仍然希望(4)是直到x为止的素数个数的一个好的估计，说不定改用另外的论据就能给出一个小得多的误差，结果也就是这样的。事实上，误差绝不会比(4)式大很多。然而，当y=√x时，直到x为止的素数的个数是(4)式的8/9倍。

那么(4)式为什么就不是一个好的估计呢？在筛去素数p时，我们曾经假设在余下的整数中，大约每隔p个就删除一个。仔细的分析会说明，当p很小时，这是有根据的，但是对于p变大的时候所发生的情况，这就是一个越来越差的近似了。事实上，当y大于x的某个幂时，(4)式并不给出一个正确的估计。那么，错在哪里呢？前面一直有一个设想，即筛去的整数在余留下来的整数中所占比例大约是1/p，但是这个设想后面隐藏了一个没有明说的假设，即筛除素数p的结果与以前筛除小于p的素数时发生的情况无关。但是，如果我们考虑的素数不是很小，这个假设是错误的。估计直到x为止的素数的个数之所以困难，这是主要理由之一，而事实上，在许多相关的问题的核心困难也与此类似。

我们可以把上面给出的界限精细化，但是似乎不能得到素数个数的渐近估计（即一个只差一个因子就成为正确的估计，而且这个因子当x变大时趋于1）。关于这种估计的第一个好的猜测出现在19世纪初，但是并不比高斯从自己的观测所得出的结果更好，高斯在16岁时研究了直到300万的所有素数的表，并且得出结论说“直到x为止的素数的密度大约是1/logx”。为了解释这一点，我们猜想直到x为止的素数个数大约是

现在把这个猜测（每一项都舍入成为最接近的整数）与最新的关于素数的数据做一个比较。这些数据是天才与计算能力的混合产生的。表1给出了直到10的各次幂的素数的真实数目，以及它们与高斯的公式给出的数的差。

这里的差远小于这些数本身，所以高斯的预测惊人地准确。高斯似乎总是估计得多了一些，但是既然表的最后一行的宽度只有第二行的一半，所以这里的差应该大约为√x。

在1930年代，伟大的概率论专家Harald Cramér给出了高斯的预测的概率论解释。我们可以把正整数中的素数和合数分别用1和0来表示，如果从3开始，每遇到一个素数就写一个1，遇到合数则写一个0，这样从3开始的正整数序列就成了

也就是

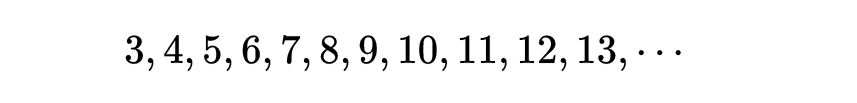
Cramér的思想是假设这个表示素数和合数的01序列有着“典型的”01序列的性质，并且利用这一点来对素数作出精确的猜测。更精确地说，设X_3，X_4，…是一个随机变量的无限序列，这些随机变量取值0和1，而令X_n取1为值的概率是1/logn（所以它等于0的概率是1-1/logn）。又设这些随机变量是独立的，所以对于每一个m，对于X_j，j≠m的知识不能告诉我们任何关于X_m的知识。Cramér的建议是，任何关于1在这个序列中的分布的命题为真，当且仅当它对这个随机序列以概率1为真。在解释这个命题时需要小心。例如任意随机数列必以概率1含有无穷多个偶数。然而，现在有可能提出一个考虑到这样的例子的一般原理。

下面是应用这个高斯-Cramér模型的例子。可以应用中心极限定理来证明在我们的序列的前x项中有

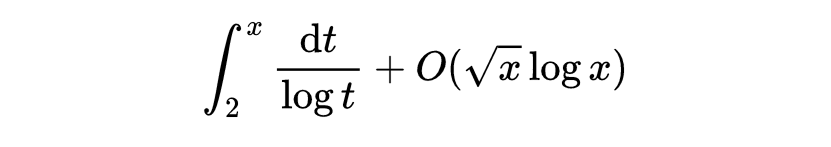
项是1的概率为1。这个模型告诉我们，对于表示素数的序列这个预测也是真的，所以我们预测

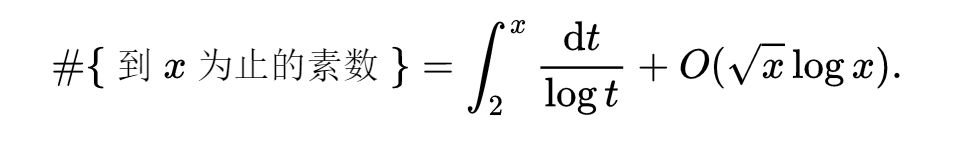
表1正是说明了这一点。

高斯-Cramér模型提供了一种思考素数分布的漂亮的方法，但是它并没有提出证明，好像也不大可能把它变成一个可以提供证明的工具。在解析数论里面，我们总倾向于计数那些自然地出现在数论中而又很难计数的对象。迄今为止，关于素数的讨论集中在从素数的基本定义和少数几个基本性质——特别是算术的基本定理——来得出上界和下界。这些界，有的很好，有的则不怎么样。为了改善这些界，先要做一些看起来不那么自然的事情，而把我们的问题重新陈述为关于复函数的问题，这使我们可以动用分析中的深刻的工具。