大家好!本文和大家分享一道2006年湖北高考数学真题。这道题综合考查了二次函数的图像与性质、基本初等函数的求导、递推法求数列通项公式、裂项相消求数列的前n项和以及求参数的取值范围等知识。这道题看起来难度挺大,但是掌握方法后其实并不难。

先看第一小问:求通项公式。
显然,本题考查的是递推法求数列的通项公式,所以首先要找到递推关系。
要找递推关系,就要先求出二次函数f(x)的解析式。由于二次函数f(x)的图像过原点,所以f(x)的解析式中的常数项为0;又因为f'(x)=6x-2,所以可以得到f(x)的解析式为f(x)=3x^2-2x。
根据题意,就可以得到:Sn=3n^2-2n①。也就是说这个递推关系是Sn关于n的一个关系式,而此类递推关系求通项公式的方法很简单,就是利用an=Sn-S(n-1)求解。即由①可得:S(n+1)=3(n+1)^2-2(n+1)②,②-①即可得到a(n+1)的表达式,从而进一步求出an的通项公式。

上图解题过程是先求出a(n+1)再求an,为什么要这样做呢?因为如果直接求an,很多同学会忘了验证当n=1时是否满足求出的通项。
如果直接求an,那么就要用到an=Sn-S(n-1)的关系,此时就有一个限制条件,即n≥2,所以需要验证n=1的情况。
另外,由于数列{an}的前n项和是一个关于n且不含常数项的二次函数,那么该数列一定是等差数列,由此可以快速判断结果是否正确。

再看第二小问:求参数的最值。
由第一小问可知:an=6n-5,所以bn=3/[(6n-5)(6n+1)]。
很明显,要求bn的前n项和就要用到裂项相消法,所以需要先将bn的通项公式进行变形,即bn=[1/(6n-5)-1/(6n+1)]/2,从而可以求出Tn=[1-1/(6n+1)]/2。
Tn<m/20,即[1-1/(6n+1)]/2<m/20。显然,在n为正整数的范围内,[1-1/(6n+1)]/2是小于二分之一的,所以m/20≥1/2,解得m≥10,即m的最小值为10。
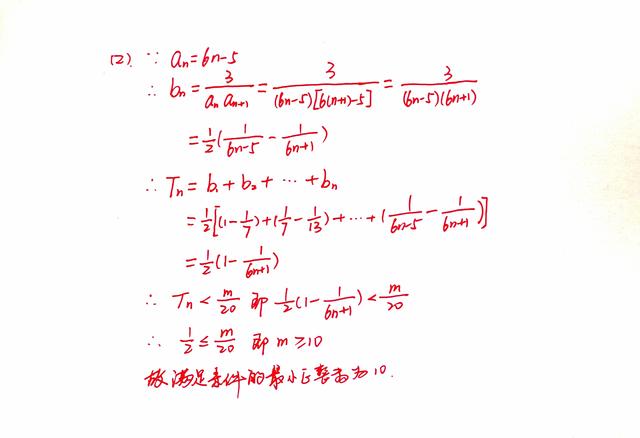
当然,不少同学计算到Tn=[1-1/(6n+1)]/2时会继续进行化简,最终得到Tn=3n/(6n+1)。接着,由Tn<m/20可以得到:m>60n/(6n+1)。一些同学做到这步就不知道怎么做了,其实只需要分离常数,即m>10-10/(6n+1)。
由于10-10/(6n+1)肯定大于10,所以m≥10,即可求出m的最小值。

这道高考真题看起来比较难度很大,但是掌握方法后其实并不难。你觉得呢?
