本篇文章主题：量子力学之路（2）——开普勒与牛顿

量子力学之路（1）——坚实的数理基础至关重要，没有捷径可走

这篇文章将比一般文章更长，因为我要建立牛顿力学和天体力学。我要提前提醒你们，这个推导过程会很繁琐，但不会跳过重要步骤，并且在逻辑上尽可能地少一些不直观的跳跃。

本系列将对物理学中的重要概念进行大量解释。不幸的是，要找到帮助我写本系列文章的资源很困难。某些主题和推导的基本步骤在大多数资源中被省略，特别是在经典力学中。

自我检查一下，是否能理解或解决一下的几个问题：

1、开普勒第三定律

利用椭圆面积的公式和开普勒第二定律的形式来推导开普勒第三定律。需要解出角动量，万有引力常数，太阳的质量，物体的质量，偏心率，角动量的长半轴方程。

2、正圆

找出轨道为正圆的条件。换句话说，使ρ为常数。

3、多体和质心

假设有N个相互作用的物体遵循牛顿运动定律。表明质心以恒定速度运动。

4、齐奥尔科夫斯基火箭方程

假设在太空中有一枚火箭，附近没有任何东西，也没有空气阻力。它通过在尾端排放恒定速度（ve）的尾气来运动。如果开始的质量是M，结束的质量是m，求出总的速度变化量。你可以假设火箭不会转动，但要注意动量必须守恒而且火箭的质量随时间变化。

自古以来，人们就一直在研究恒星。对古代的天文学家来说，大多数恒星并没有相对运动。而且古代的天文学家相信地心说，他们能够提出公式，以合理的准确性预测天体的路径。这个公式后来被证明是一个早期的傅里叶级数的例子。

这些复杂的公式与数据吻合得很好，但没有任何解释。然后是尼古拉·哥白尼，他提出了日心说模型。他的模型在概念上比托勒密的模型简单。这是朝着正确方向迈出的第一步。在仔细研究了这些数据之后，约翰内斯·开普勒提出了他的开普勒行星运动定律：

每颗行星的轨道都是一个椭圆，太阳是椭圆的两个焦点之一。

在相等的时间间隔内，连接行星和太阳的线扫过的面积相等。

一个物体的轨道周期的平方与其轨道长半轴的立方的比率是相同的所有物体围绕同一主轨道运行。

艾萨克·牛顿

根据开普勒定律，我们知道行星是怎么运动的，但不知道为什么会这么运动。这需要几位科学家的努力，最著名的是艾萨克·牛顿，提出了一个完整的解释。在开普勒之后的几十年，牛顿发表了他的《自然哲学的数学原理》(简称《原理》)，其中有三个基本的命题：

牛顿的三大运动定律。

地球上的物理定律可以应用于天体。

重力是一种引力，作用于所有质量之间，与物体的质量成正比，与物体之间距离的平方成反比。

根据这三个命题，牛顿能够解释开普勒定律和许多其他物理学上的其他问题。

动量

现在我们已经了解了一些历史信息，让我们来看看动量。在经典力学中，动量是一个矢量，等于物体的质量乘以它的速度。牛顿的三个运动定律都是关于动量的表述。

牛顿三大运动定律

运动中的物体将保持运动状态，除非受到外力的作用。

力是动量的时间导数。

每一个力都有一个大小相等、方向相反的反作用力。

第一定律说，一个不与其他物体相互作用的物体将有一个恒定的动量，因此有一个恒定的速度。第二定律定义了力如何改变物体的动量。它比第一定律更普遍，但牛顿明确指出，第一定律是对亚里士多德物理学的直接回应。最后一个定律保证了如果两个物体相互作用，那么它们动量的总和将是守恒的，即使它们各自的动量可能不守恒。

牛顿万有引力定律

这是一个很好的公式，但它缺乏坐标信息和方向。我们可以把牛顿的万有引力定律写成

其中F_21是第一个物体对第二个物体的作用力，G是常量，m_1和m_2是两个物体的质量，s_1和s_2是两个物体的位置，|s_1- s_2|是两个物体之间的距离。从数学上讲，s_1- s_2表示从第二个物体的位置到第一个物体的矢量，矢量的大小用绝对值表示。这个表达式看起来很奇怪，因为分母是距离的3次方。但是分子式中的s_1- s_2也是距离单位。对于作用在一个物体上的总力，我们可以把每一个物体对第一个物体施加的力加起来。

用牛顿力学和牛顿万有引力定律来推导开普勒定律。要做到这一点，我们需要找出运动方程，这是一组描述物体如何作为时间的函数运动的微分方程。在牛顿力学中，要找运动方程需要

找出所有作用在物体上的力，

求出坐标系中的加速度，

把第一步中的力写成系统中每个物体的位置和速度的函数，

让置步骤2和步骤3的结果相等，

匹配基向量的系数。

这样，你以得到每个物体的三个微分方程（如果考虑到力矩，还可以得到一些额外的方程）。

步骤1：寻找力

让我们从太阳系中的任意一个天体开始。根据牛顿万有引力定律，有

如果代入一些数字，会发现可以忽略除太阳以外的所有项。例如，太阳对地球施加的力是月球对地球施加的力的177倍。木星对土星施加的力，是除太阳以外的任何两个物体之间最强的力，它只占土星和太阳之间力的0.5%左右。

只要考虑太阳对任意物体施加的力

根据牛顿第二定律，有

假设物体的质量是恒定的

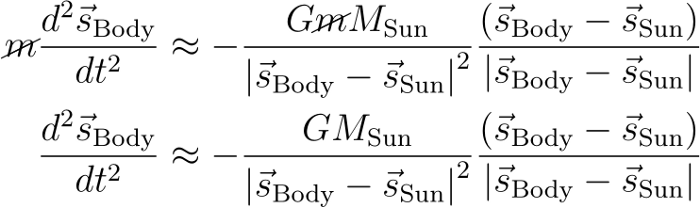
初步的简化

至此，我们已经知道了运动方程，但还可以做一些简化。首先，注意到太阳比太阳系中任何其他物体的质量都大得多。根据牛顿第三定律，尽管两个物体受到的力是相同的，但太阳的移动要比其它物体小得多。这样，我们可以将坐标系统的原点设置在太阳的中心，这意味着太阳的位置是零矢量：

如果用笛卡尔基向量写出物体的位置，有

角动量

我们要让其中一个坐标为零。假设z = 0。根据上面的方程，物体在z方向上不会受到任何力，因此也不会有加速度。如果z方向的速度也是0，那么z将保持为0。

我们总是可以选择坐标轴，使z方向上的位置和速度总是为零（让z轴垂直于初始速度和初始位置）。为了做到这一点，我们使用向量积（外积、叉积），得到一个垂直于另外两个三维向量的三维向量。两个向量的向量积的长度与这两个向量的长度以及它们之间夹角的正弦有关。

如果我们取物体的位置矢量和速度矢量的向量积，然后把结果乘以质量，就得到了角动量，它有类似于动量的性质，但是是围绕着一个点旋转而不是平移。我们稍后会看到，开普勒第二定律是角动量守恒的结果。现在，我们要用它来定义z基向量。

步骤2：在柱坐标中寻找加速度

因为z将保持为0，并且我们在处理一个旋转的问题，使用柱坐标再合适不过了。清楚起见，我们仍然需要在柱坐标中定义x轴和y轴，但不会被涉及到它们的计算中。因为我们选择了柱坐标，位置被定义为

你可以通过在笛卡尔坐标系中展开来验证。

求位置的二阶时间导数，有

因为是柱坐标，因此ρ和φ基向量不是常量，这意味着我们也要对它们求时间导数。

惯性力

在任何加速的坐标系中，必须引入加速度项（惯性力）来抵消坐标系的加速度。在我们的例子中，有两个惯性力:

离心加速度

科氏加速度

虚力

惯性力也被称为虚力，因为这些力与物体之间正常的相互作用无关。

举个例子，离太阳系最近的恒星大约在4光年之外。如果定义我们的坐标系统与地球一起旋转，那么这颗恒星将以大约10000倍的光速运动，并具有相同量级的恒定加速度。即使不考虑相对论，这个结果也是荒谬的（与任何物体都没有物理上的相互作用，却有巨大的速度和加速度）。

但如果我们让x轴从地球指向恒星，恒星就不会移动，也不会有加速度。

话虽如此，我并不喜欢“虚力”这个名字，因为它会让人产生一种错误的印象，认为它们不能代表真实的东西。例如，当汽车加速时，一个虚力会把你推向座位上，所以它并不总是“虚”的。

惯性力是非惯性参照系的产物，它们出现在了加速度项中。所有的惯性力都与物体的质量成正比。

步骤3：在柱坐标中写出引力

我们已经把质量和引力分开了，所以只需考虑加速度。我们必须把重力加速度转换成柱坐标

步骤4和步骤5：设力的两个定义相等，并比较基向量

现在可以找出具有相同基向量的项，这可以帮助我们将它们与柱坐标下牛顿引力进行比较

这个结果给出了两个运动方程。第三个运动方程是z(t) = 0。

角运动方程

根据一阶微分方程的知识，我猜这个方程是两个函数乘积的时间导数。我们从标准乘积法则开始

在这种情况下，可以让g(t) = φ ' (t)。为了让它成立，我们需要将方程乘以某个函数μ(t)

解出这个方程

函数μ(t)被称为积分因子。如果你不知道，我建议你开始学习微分方程微分方程第一步，吃透基本概念——复数，多项式方程及矩阵理论​。把所有东西都代进去

这意味着f(t) g(t) = ρ^2φ '。我们试着对ρ^2φ '求导

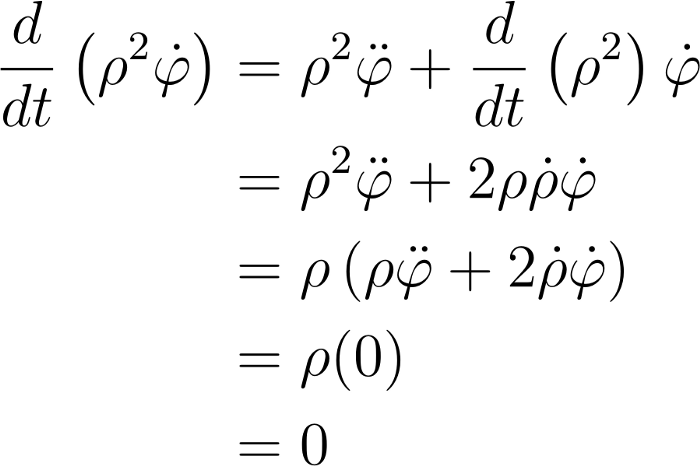
这个结果似乎是成立的，我们已经将方程简化到可以对两边积分的程度

你怎么知道它是一个乘积的时间导数的？

求解微分方程，首先要猜测解的形式，看看能不能解出来。如果不能，再另一种形式。令人恼火的是，许多关于微分方程的课程（资源）只给出了可行的猜测，这就给人制造了一种错觉，以为某些作者（编者）一下知道了解的形式。现实中，他们尝试了各种形式的函数，直到得出正确的解。

角动量守恒

我们要加一个常数，但应该加什么常数呢？在本文的前面，我提到了角动量，但没有计算它。现在计算它，得到

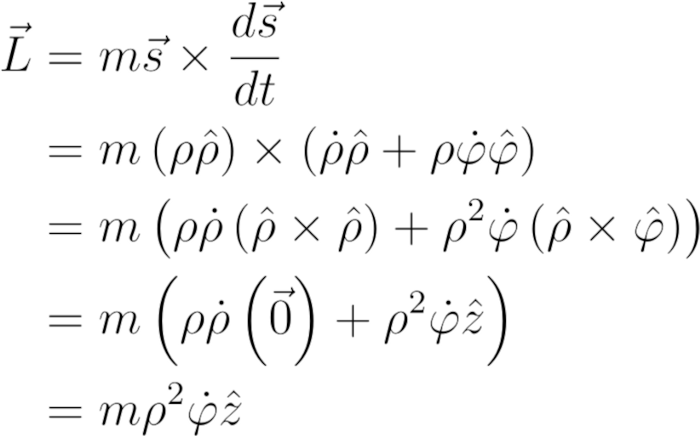
角动量等于质量乘以ρ^2φ '（在z方向上）。因此，C=L/m。此外，角方程还可以帮助我们解径向方程

要清楚的是，我们还没有解出角方程，但是我们可以用它来去掉径向方程中的一些烦人的因素。

开普勒第二定律

在讨论径向方程之前，我们先来推导一下开普勒第二定律。我们知道函数ρ(φ)在两个角度φ_1和φ_2之间的面积是

让τ表示它达到φ_1和达到φ_的时间间隔。如果我们做u代换，有

从角方程，我们知道ρ^2φ ' = L/m，所以可以把它代入积分

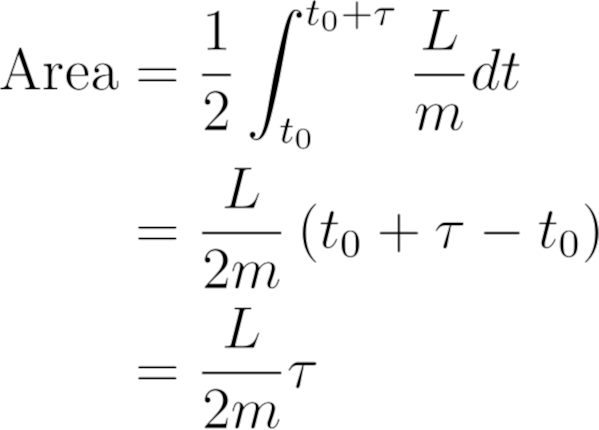
注意，除了从一个角度到另一个角度所需的时间是τ外，我们没有对这两个角度做任何说明，这就证明了开普勒第二定律。

径向方程

把角方程的解代入得到

这个方程和伯努利微分方程很相似。非线性项的二阶导数会引入无法抵消的项。为了解决这个问题，我们将放弃寻找ρ(t)和φ(t)的封闭解，而尝试寻找它所走的路径，ρ(φ)。

追踪路径vs.位置的时间函数

为了强调这一区别，我们可以考虑一些以不同方式在赛道上前进的人：

开赛车，

骑自行车，

步行，

在赛道上走了一半，然后转身，

所有这些都可以有不同的ρ(t)和φ(t)，但它们都有相同的ρ(φ)。同样地，只要知道ρ(φ)，太阳系中的行星和其他天体就有可能以随机的速度运动，旋转，甚至是瞬移，只要它们一直在轨道上。为了确定行星的运动方式，我们还需要φ(t)，这可以从角方程中得到，目前还没有解出来。

伯努利方程

在伯努利方程中，我们会猜想ρ(t)是α(t)的幂

如果求一阶导数

这个表达式看起来没什么问题，我们来求二阶导数

正如你所看到的，有一个导数的平方，它阻止了我们求出闭合解。我们还没有设n的值，所以看看是否可以将它设为某个值，以去掉平方导数。如果n = 0或n = 1，就可以消去平方导数，但也会把有用的东西消去。我们注意到平方导数来自于一阶导数中的α项，所以看看能不能去掉它。我们用链式法则把dα/dt写成(dα/dφ) (dφ/dt)。从角方程，我们知道dφ/dt = L/(m ρ^2)，从α的定义，有

为了消去α项，需要- n - 1 = 0，也就是n = - 1，这就得到

现在，我们可以求二阶导数

我们用了和上面一样的技巧，把所有东西都写成φ的形式。把这个方程和α的定义代入径向方程，得到

该微分方程是一个标准的二阶线性微分方程，我们可以用多种方法求解。这篇文章已经很长了，我们直接写出解

选择坐标轴

前面提到过，在得到解之前，x轴和y轴并不参与计算，我选择它们使sin项消失而cos项保留。这样，我得到了α(φ)的一个更简单的方程

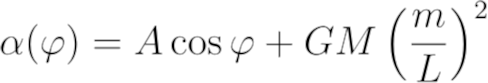
我们要找的不是α(φ)而是ρ(φ)，根据α的定义，有

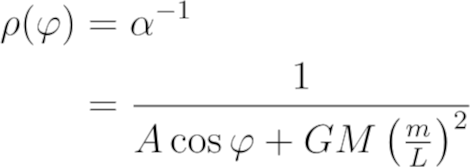
可以把它提出来，得到一个焦点在原点的圆锥曲线的标准形式。

圆锥曲线是通过切割圆锥得到的形状

圆（ε = 0）

椭圆（0 < ε < 1）

抛物线（ε = 1）

双曲线（ε > 1）

特别值得注意的是椭圆。请注意，抛物线和双曲线都将走向无穷远，所以任何沿着抛物线或双曲线轨道运行的物体都不会留在太阳系中。然而，这些行星仍然存在于太阳系中，这意味着它们要么是圆形，要么是椭圆形。因为圆只能在ε的一个值出现，所以几乎肯定会得到一个有界轨道的椭圆。换句话说，我们已经证明了开普勒第一定律。

位置作为时间函数的闭合解

我们可以把ρ(φ)代入角方程得到

这个方程的解至少需要，椭圆积分。你不会从这个方程中得到一个封闭的解。

轨道的特点

现在，我们来计算一些关于轨道的事实。我们想知道一些有用的信息，比如两个物体之间轨道的最远点和最近点。我可以看到最大值和最小值出现在

半长轴和半短轴

对于椭圆轨道，我们也可以计算半长轴和半短轴，你可以把它们想象成椭圆的两个半径。

从这些轴，我们可以用一个简单的公式来计算椭圆的面积：

在偏心率为0的极限情况下，得到了一个圆。

动量守恒

太阳静止的假设导致动量守恒的一些问题。绕轨道运行的物体会改变它的速度，而“太阳是静止的”，这就意味着动量不守恒。为了保证动量守恒，我们需要太阳移动。如果我们从距离矢量q = s_1- s_2开始，求它的二阶时间导数，有

从这一点开始，M和m是两个物体的质量。从第三行到第四行，使用了牛顿第三定律。

这和开始时的方程大致相同，但是减少了质量μ。我们也可以看看总动量如何随时间变化，

根据牛顿第三定律，它是守恒的。如果我们定义空间中的一个新点

会发现

我们称Q为质心。一组没有外力的物体的质心将以恒定的速度运动。我们可以通过解线性方程组，找到用这两个新量表示的原始轨迹。

我们已经讨论了经典力学

现在我们已经建立了牛顿力学，而且可以用牛顿力学解决经典力学中的任何问题。不幸的是，牛顿力学有一些问题。

找到守恒量会使问题变得容易得多。幸运的是，我们发现角动量是守恒的。

我们必须计算基向量的时间导数。

在解决问题之前，我们必须知道所有的力，这可能很困难。

试图在其他坐标系中重写运动方程是很困难的。

牛顿力学需要大量的几何理解。

牛顿力学不能很好处理的经典问题是，珠子（球珠）只能沿着弯曲成某种形状的金属线移动。应该只有一个运动方程来表示珠子沿着导线应该移动多远。在牛顿力学中，系统中每个物体都有三个运动方程。此外，你还必须考虑线对珠子施加的力，以保证它在电线上，这是一个复杂的问题。你可能甚至不能把力写成一个封闭的形式。有这些约束力的系统随处可见，所以我们不能忽略它们。为了解决这些问题，我们需要一些新的框架。

下一步是什么？

在接下来的几篇文章中。我们将跳出力和矢量框架，转而关注能量和标量（新的框架），从不同种类的势能和描述它们的偏微分方程开始。