随机微积分是数学的一个分支，主要研究随机过程（如时间上随机的过程或服从某些统计性质的随机变量序列）及其相关的微积分。它在工程、科学、定量金融和精算科学中有许多应用。这是一个很难学习的学科，因为大多数关于这个主题的书都假设读者是一个数学家，拥有大量抽象数学的知识。

在这篇文章中，我将描述随机积分最基本的组成部分，维纳过程W(t)，这需要读者熟悉基本的统计和概率概念，诸如概率分布、随机变量的统计矩和矩量母函数等。

W(t)的基本性质

维纳过程W(t)也被称为布朗运动，是一个时间上的随机过程，具有以下统计性质，

其中E[…]表示均值或期望值，Var[…]表示方差。本质上，整个过程在时间t上的均值为0，但它的方差随时间线性增加，也就是说，时间越长，方差越大。我们可以把它想象成一个受到随机力作用的粒子。时间过得越久，就越难预测它的位置。例如，如果我们考虑一个一维轨迹（仅向左或向右运动），并且质点的位移表示为X(t)，那么当质点受到维纳过程（例如在每个时间点随机轻推）时，位移X(t)将具有如下图所示的样本轨迹。

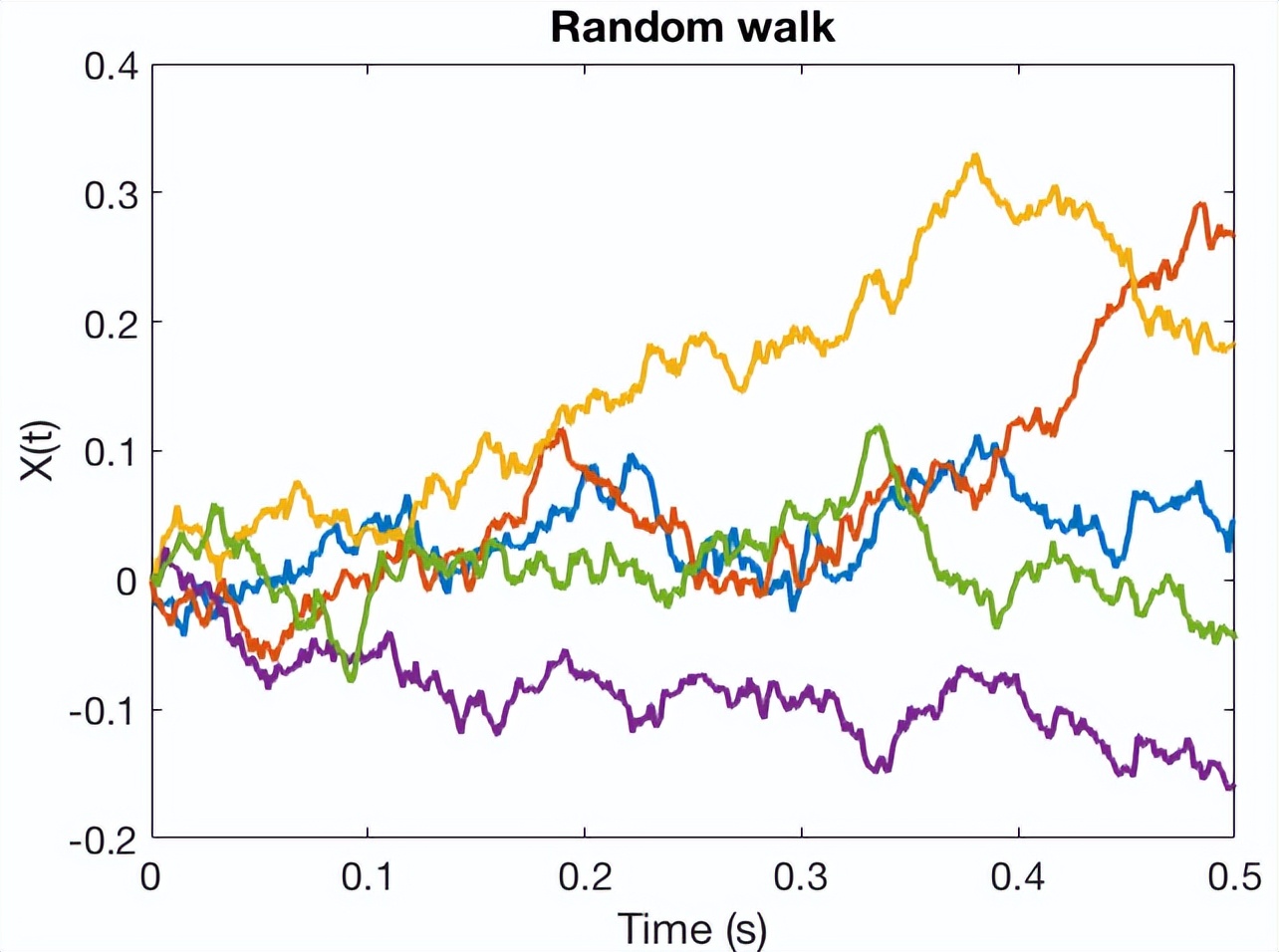
受一维维纳过程样力作用的粒子随机轨迹。

类似地，维纳过程中无穷小的增量dW(t)具有统计性质

dt是一个无限小的时间步长。如果我们在离散的意义上考虑这个问题，可以将“维纳增量”建模为

其中N(0,1)是一个标准正态随机变量，均值为0，方差为1。维纳过程还有这样的性质。

对于任意两次t > s。

W (t)函数

如何计算包含随机变量的函数的统计量？例如，使用矩量母函数的概念，一个指数函数和正态随机变量的三角函数。在维纳过程的情况下，我们可以使用定义计算矩量母函数，

其中X为正态分布，均值为0，方差为1。a为任意常数，用于计算W(t)的统计矩。因此，一维的矩量母函数仅仅是函数乘以它的概率密度函数的积分（正态分布随机变量的概率密度函数为高斯分布），并被写成

使用高斯函数积分的标准结果，我们得到

由此我们可以计算W(t)的矩如下，

例如，前四个矩是

类似地，我们可以计算W(t)的其他函数的统计量。让我们看几个例子。

例1

首先利用欧拉公式将正弦函数转化为指数的和，然后利用W(t)的矩量母函数性质求其平均值，得到W(t)的正弦函数：

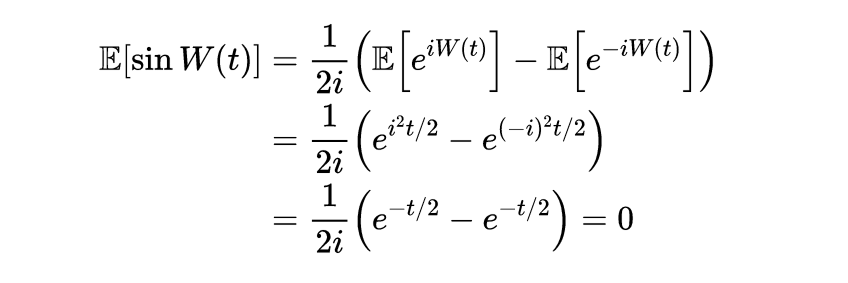
例2

让我们找到期望值的一般公式

从下面的定义开始：

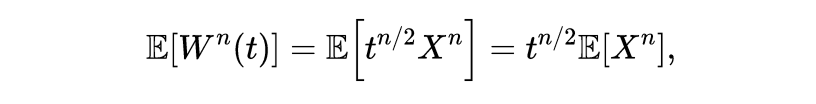
其中X是一个标准正态随机变量。然后

这里我们用分部积分法得到

最后一个表达式可以使用递归关系求值，得到

当n是奇数时为0。由此我们可以写

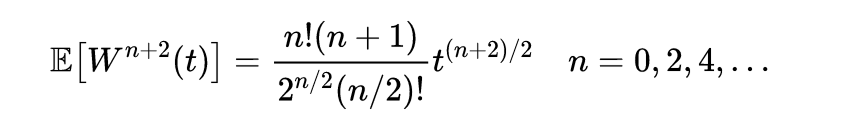
例如，我们可以用之前的结果来验证这一点

给出了我们从使用矩量母函数获得的期望结果。

例3

求过程的均值和方差

这个例子比较难，但很有趣。我们首先将函数写成泰勒级数展开，

然后应用期望运算符，

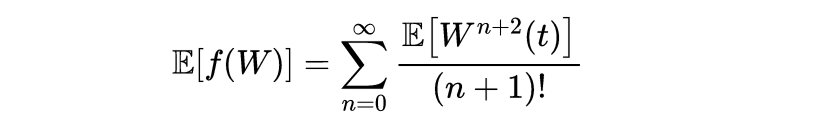
回想一下，由于W(t)是正态分布，均值为零，所有奇数矩都消失了，我们可以写出简化的表达式

现在，让k = n + 2 ，n = k - 2，我们写

得到，

因此

这个表达式可以进一步简化为

从而得到预期值的最终结果，

为了得到方差，我们从求值开始

如下

使用前面的相同结果，我们展开，

写成k = n - 1和n = k + 1

由此我们得出结论

我们可以通过计算机来验证这些确切的结果。下面是我的验证情况，我对函数f(W)采样1000次，然后计算均值和方差。对比下图所示，

均值。

方差。

当然，维纳过程还有许多其他有趣的函数，但希望我在这里介绍的例子可以作为一个好的起点。