量子信息守恒(用冯·诺依曼熵来量化)是量子力学线性和幺正性的一个基本结果。由于信息和熵这两个术语在许多科学分支中被( 可交换地)使用,这对熟悉热力学第二定律的人来说可能听起来很奇怪(热力学第二定律说熵通常随时间的推移而增加),信息和熵怎么可能是一致的呢?

对于哈密顿系统,动力学总是可逆的,所以信息是守恒的(根据刘维尔定理)。人们可能会想,如果熵是一种信息的度量,那么对于一个经典系统,熵是如何增加的?
哈密顿系统是一个受哈密顿方程支配的动力系统。在物理学中,这个动力系统描述了物理系统的演化,如行星系统或电磁场中的电子。这些系统可以用哈密顿力学和动力系统理论来研究。
刘维尔定理是经典统计力学和哈密顿力学中的一个关键定理。它断言相空间分布函数沿系统轨迹是恒定的。
简短的回答
刘维尔定理所描述的熵(或信息)与第二定律所讨论的熵并不相同。后者是指隐藏信息的数量(宏观测量无法获取的信息),而前者是一个系统的总信息量。换句话说,热力学的不可逆性是一种统计效应,与经典力学/量子力学的可逆性并不冲突。
尽管如此,这个问题比它看起来更复杂,所以让我们深入研究一下。
什么是熵和信息?
“熵”一词在不同的环境中使用,有不同的概念。我们在信息论(香农熵)、统计热力学(玻尔兹曼熵)和量子力学(冯·诺伊曼理论)中发现了熵。虽然它们都用相同的公式定义,但它们描述了不同的概念。

玻尔兹曼将熵定义为一个符合系统宏观条件(宏观状态)的可能微观状态的数量的度量。冯·诺伊曼后来将熵的概念从经典统计力学扩展到量子信息论,克劳德·香农发展了类似于电信信号中信息随机损失问题的统计概念。
在物理和信息科学中,信息和熵通常可以互换使用。事实上,熵可以被认为是一个信息的量度,它是用来陈述一个系统的微观状态所缺少的(隐藏)的信息。
换句话说,热力学熵反映了观察者在宏观测量条件下对系统微观状态构型的无知。
细粒度和粗粒度熵
对系统的细粒度描述是对其微观行为的详细描述。粗粒度描述是对其一些细节进行平滑处理的描述。这种平滑让观察者忽略了系统精确微观状态。例如,像温度和压力这样的热力学量是粗粒度描述的结果,因为它们将许多粒子的性质平均为几个宏观变量。
由于量子系统通常由它们的所有粒子描述,冯-诺伊曼熵通常是细粒度的,因此在量子刘维尔定理下是常数。另一方面,从观察者的角度来看,系统的粗粒度信息的数量可能会随时间的变化而变化。粗粒度熵因此可以被视为“观测熵”或“热力学熵”,因为它测量了观察者所测量的宏观状态下隐藏的信息。
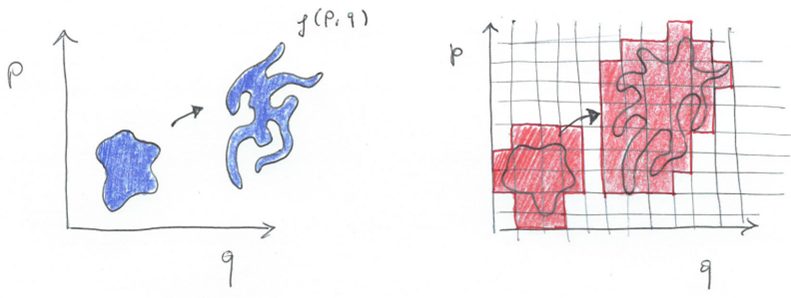
粗粒度熵的抽象表示。(左)变换后的相空间体积保持不变,但从观察者的角度来看,体积会增加,因为观察者只能看到相空间的网格表示(右)
这种粗粒度似乎相当抽象。为了更好地理解,让我们想象粒子在房间里膨胀的例子(初始状态下,粒子都在左下角)。作为观察者,我们可以把房间分成划分为“三维网格”,然后计算每个网格里粒子的数量。假设最高熵态对应于所有网格都包含相同数量的粒子的情况,我们可以这样计算熵:

其中Ni为每个盒子里的粒子数。
有趣的是,计算出的熵取决于网格分辨率。随着分辨率的增加,我们对系统的了解也逐渐增加,直到网格的尺寸非常小,我们对所有微观状态都有了完全的了解。在这种情况下,由于隐藏信息总是零,熵保持不变。
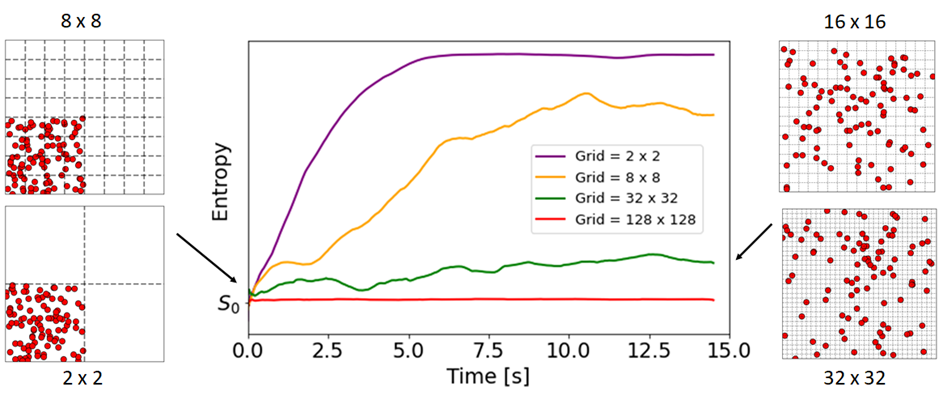
对不同的网格分辨率(因此不同的宏观状态变量),计算熵。
从这个例子可以清楚地看出,热力学熵是与观察者相关的,它的值取决于观察者所能获得的信息。
尽管如此,仍然可能存在一些因素,阻止任何观察者获得细粒度系统的信息。观察者“可获得信息的极限”的存在将定义一个客观的基本粗粒度,热力学第二定律将成为一个基本定律,而不是一个明显的现象。例如,在量子力学中,几乎不可能在不破坏(影响)系统的情况下测量一个状态,这使得量子纠缠成为这种基本粗粒度的一个很好的候选。
热力学第二定律和量子纠缠
为什么粗粒度熵会增加?
由上面描述的粗粒度形式。我们可以得出这样的结论:粗粒度熵的增加反映了观察者对系统知识的丢失。根据热力学第二定律,我们对宇宙的粗粒度描述对其微观状态的描述越来越不精确,这种现象被称为“模糊”。这种模糊机制背后的确切性质仍然不清楚。

量子不确定性随着粒子变得越来越纠缠而增加,导致观测者可获得的信息丢失。
Lloyd在1988年提出了一个很好的解释。他意识到,量子的不确定性,以及它随着粒子变得越来越纠缠而增加的方式,可能是模糊机制的真正来源。在他看来,信息会变得越来越分散,但它永远不会完全消失。所以,虽然局部的熵增加了,但整个宇宙的熵保持为零不变。假设宇宙是一个封闭的系统,它是一个纯状态。但它的个别部分,因为它们与宇宙的其他部分纠缠在一起,是混合的。这意味着各部分的熵的增长被不断增长的负纠缠熵抵消。纠缠熵(Sen)没有可测量的结果,热力学第二定律(Sobs)描述的熵是我们可以监测的:
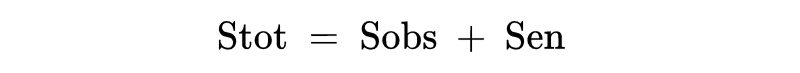
虽然从技术上讲,熵永远不会是负的,这里Sen是给定可观察态(O)的隐态(H)的条件熵,对于量子系统,它可以取负值。


量子退相干是导致粗粒度熵增加的一个很好的例子。
这可能会让人感到困惑,让我举一个简单的例子。量子纠缠在物理实验和量子计算中是有用的。由于统计学的原因,与环境接触的量子系统在一段时间后不可避免地发生退相干。这种纯度(或“量子性”)的丧失是通过系统与其环境之间的纠缠来调节的,这种纠缠是不受控制和不可测量的。结果,关于初始系统的部分信息实际上永远丢失给了观察者,从而增加了它的可观测熵,使这个过程实际上不可逆。但是,系统的状态会继续受到与环境纠缠的约束,所以退相干后的细粒度熵没有变化。
波函数坍缩和黑洞
最后,我想讨论波函数坍缩和黑洞,这些问题可能与上面讨论的矛盾。到目前为止,我们假定信息守恒的原则在宇宙中始终成立。然而,在某些情况下,信息可能是不守恒的,因此,即使是宇宙的细粒度熵Stot也可能不可逆转地增加。

在量子力学中,波函数坍缩因“非幺正变换”而闻名,它会破坏信息。同样,黑洞也可能通过霍金辐射以不可逆的方式破坏信息。这种信息在黑洞中永久消失的过程被称为黑洞信息悖论。然而,量子弦理论表明,信息是通过全息原理或黑洞的量子描述而守恒的。另一种理论认为,黑洞可能会在其半衰期前后经历一个相变,在这个过程中它们会开始失去信息。
结论
熵可能是物理学中最神秘、最难理解的概念之一。自然界中发现的几乎所有系统都不处于热力学平衡状态,因为它们不断地受到来自其他系统的物质和能量流动的影响。
在这篇文章中,我介绍了粗粒度熵的概念,并给出了热力学第二定律与量子纠缠的一些解释。然而,并不是每个人都同意这些概念。例如,有些认为,由于粗粒度熵总是依赖于观察者选择的宏观变量,因此熵的增加是知识有限的观察者的主观测量,而不是一个基本量。另一些人认为粗粒度是海森堡不确定性原理的基本结果,细粒度熵在本质上永远不能为宏观系统计算。
这篇文章是我关于熵和热力学第二定律系列的第二部分。感兴趣的可以看看第一部分这个世界上(可能)只有4、5个人真正理解熵,我不属于他们。
