数学中有许多问题，要求在各种约束之下，使某个量最大化或最小化，这些问题称为极值问题。和计数问题一样（数学不好，你连“简单”的计数都不会，计数问题凭什么这么难？），有一些极值问题可以实际地算出精确解来，而更多的则是，虽然精确解是谈不上的，但仍然可以找到有趣的估计。这两类问题，下面各有一些例子。

（1）令n为一正整数，而X为一含有n个元素的集合。问可以找出X的多少个子集合，使得没有一个会含于另一个子集合之内。

可以做出的一个简单观察是∶如果两个不同子集合大小相同，则没有一个会包含于另一个之内。所以满足问题的约束的方法之一是选取所有的子集合具有同样大小 k。X的大小为k的子集合一共有n!/k!（n-k）!个，这个数通常记为

而不难证明当k=n/2（若n是偶数）或者k=（n±1）/2（若n是奇数）时，它取最大值。为简单计，我们集中于n为偶数的情况。刚才证明了∶在n元素的集合中，可以做出

个 n/2元素的子集合，其中没有一个会包含任意另一个。也就是说，

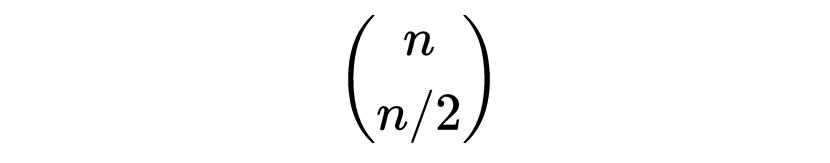
是这个问题的一个下界。一个称为 Sperner 定理的结果指出，它也是一个上界。就是说，如果取多于

个子集合，不论怎样取，其中必有一个包含于另一个之内。

（2）设有一条有重量的链子，两端挂在天花板的两个钩子上，而除此以外链子再没有其他支撑点。这个挂着的链子将是什么形状？

初看起来，这并不像是一个极大极小问题，但它很快就是了。这是因为物理学的一个一般原理告诉我们，链子将会静止在一个使得位能为最小的形状上。 这样我们就面临一个新问题∶令A，B是（位于同一水平高度而）相距的距离为d 的两点，c为长度为l以A，B为两端的曲线的集合，问哪一条曲线C∈c具有最小位能？这里设任意曲线段的质量正比于其长度。这条曲线的位能是mgh，m是曲线的质量，g是引力常数，而h为曲线的重心的高度。因为m和g不会改变，这个问题就有了一个新的陈述∶哪一条曲线C∈c具有最小的平均高度？

这个问题可以用一种称为变分法的技术来解决。粗略地说，它的思想是∶有了一个集合c，又有了一个定义在c上的函数h，即平均高度，此函数把每一个C∈c 映为其平均高度。我们试着来使h最小化，而处理这个问题的一个自然的途径是设法定义某种导数，然后再去找一条曲线C∈c，使得这个导数为0。注意，“导数”一词在这里并不是沿着曲线运动时高度的变率，而是指曲线的平均高度（以线性方式）对于整个曲线的微小摄动的响应。利用这一类的导数来求最小值，比求定义在R上的函数的驻点要复杂一点，因为c是一个无限维的集合。然而这个途径还是能起作用的，解也是知道的，是一种称为悬链线的曲线。这是又一个能够准确回答的最小化问题。

变分法的典型问题都是求一条曲线、一个曲面或者更一般种类的函数，使得某一个量达到最大或最小值。如果这个最大或者最小存在（对于一个无限维集合，它们绝非自动存在的），则使得最大或最小达到的对象，会满足一组偏微分方程，称为欧拉-拉格朗日方程。

（3）在1和n之间可以找到多少个数，使得其中不会有3个构成等差数列？如果n=9，答案是5。因为在1，2，4，8，9这五个数中，找不到3个成为等差数列。所以，在1到9之间有五个数，其中没有等差数列。那么，在1 到9之间能否找到6个数使其中不会有3个数的等差数列呢?这也不会。原因如下∶

如果这6个数中已经包含了5，那么必须舍去4或6。否则，4，5，6就是3个数的等差数列。类似地，必须舍去3与7之一，2与8之一，1与9之一。总之要舍去4个数，而只剩下5个，与题设的6个数发生矛盾。总之，这6个数中不能有5在。

我们又必须舍去1，2，3中的一个数，如果一个都不舍，则又出现了等差数列1，2，3，同理也必须舍去7，8，9中的一个。但是，我们已经不允许取5，所以4和6都必须保留。但是那样一来，就不能保留2或8。也必须舍去1，4，7之一，总之必须舍去至少4个数，而不可能留下6个数。

当n=9时，这种笨拙的逐个情况逐一论证的办法还算行得通，n 稍微大一点，就无法逐一考虑了。对于这个问题，似乎没有一个干净利落的答案准确地告诉我们，在1到n之间最大的不包含长度为3的等差数列的集合是什么，所以我们代之以寻求这个集合的大小的上下界。为了证明一个下界，必须找到一个好的构造、一个不包含任意等差数列大集合的方法；而为了证明一个上界，就必须证明∶任意的有一定大小的集合，必定含有一个等差数列。

至今为止，离最佳的界还很远呢。1947年，Behrend找到了一个大小为

其中没有等差数列，而在1999年Jean Bourgain又证明了每一个大小为

都含有一个等差数列。当n=10^100 时，

（4）理论计算机科学是许多最小化问题的来源∶当人们编制一个计算机程序以完成一项任务时，他就会希望在尽可能短的时间里完成它。下面是一个听起来很初等的例子∶如果想把两个n位数相乘，需要多少步？

即使对于什么叫做一“步”并不太清楚，也能看到通常的乘法，即长乘法，至少需要n^2步。这是因为在计算过程中，第一个数的每一位都会被第二位数的每一位去乘。 人们可能心想，这是必不可少的，但是事实上，有聪明的方法把问题变换一下，就能极大地减少计算机完成这类乘法所需的时间。最快的方法是用快速傅里叶变换来把计算的步数从n^2减少到

因为一个数的对数远小于这个数本身。

另一个实质上类似的问题是∶矩阵乘法有没有快速算法？要想用经典的方法把两个n×n矩阵乘起来，需要对矩阵里面的数作n^3次单个的乘法。这个问题上的突破主要来自 Strassen，他的思想是把这两个 n × n 矩阵的每一个都“平分”成 4 个

初看起来只不过是把原来矩阵的乘法化为8对小矩阵的乘法，但是这些乘法实际上是互有关联的，Strassen做了7个乘法，而8个乘法就可以由此导出了。然后就可以利用递归，就是把同样的思想用于加速这7个小矩阵的乘法，并仿此以往。

Strassen 的算法把矩阵乘法的步数的数量级从 n^3 降为

所以这已经是显著的改进，不过要当n很大时才是。他的基本的分而治之的策略后来又得到改进，最近又有了新的突破（最近，人工智能推进了数学研究的进程，揭示了矩阵乘法的新可能性）。

关于更多的这一类问题，可见计算复杂性和算法设计的数学还有一类更加微妙的最大化和最小化问题。例如，假设我们想要理解相继的素数之差的性质。这种差最小为1（2和3之差），不难证明差没有最大的，所以关于这些差似乎不会有有趣的最大化和最小化问题。

然而事实是，如果先作适当的规范化，就可以提出很吸引人的问题。素数定理指出，接近于n的素数，密度是大约1/logn，所以n附近的两个素数间平均的空隙长约为logn。如果p，q是两个相继的素数，就可以定义它们的规范化的空隙长为（q一p）/logp。这个规范化空隙长的平均值为1，但是会不会有时小得多，有时又大得多？

Westzynthius 在1931年就指出，甚至规范化空隙长也可能任意长，广泛的信念则是它也可以任意接近于0（由著名的孪生素数猜想立刻可以推出这件事），然而一直到2005年，才由Goldston，Pintz和Yildirim 证明了这一点。