在我们日常生活中，许多现象看似无序、随机，却暗藏规律。

这些现象从粒子在液体中的运动到金融市场的波动，从污染物在河流中的扩散到动物的迁徙，都可以用一种神奇的数学工具来描述，这就是著名的科尔莫戈罗夫方程。

今天，我们通过生动的故事和简单的比喻，带大家一起探秘科尔莫戈罗夫方程的起源、推导以及广泛应用。

故事开始于1827年，那时植物学家罗伯特·布朗正在显微镜下观察水中的花粉粒。

他惊奇地发现，这些微小的花粉粒在水中不断地做无规则的运动，仿佛有一群看不见的小鱼在水中游动。

这一现象后来被称为布朗运动。

模拟的大颗粒尘埃粒子碰撞到更小的粒子，而其以不同的速度在不同方向移动的布朗运动

虽然布朗当时并不知道这种运动的原因，但他的发现为后来的科学研究奠定了基础。

不过这要提点误解，其实布朗所说的花粉其实并不是花粉，而是花粉粒子中迸出的微小粒子。所以后面您的物理老师如果随口说是花粉运动，请你立刻纠正！

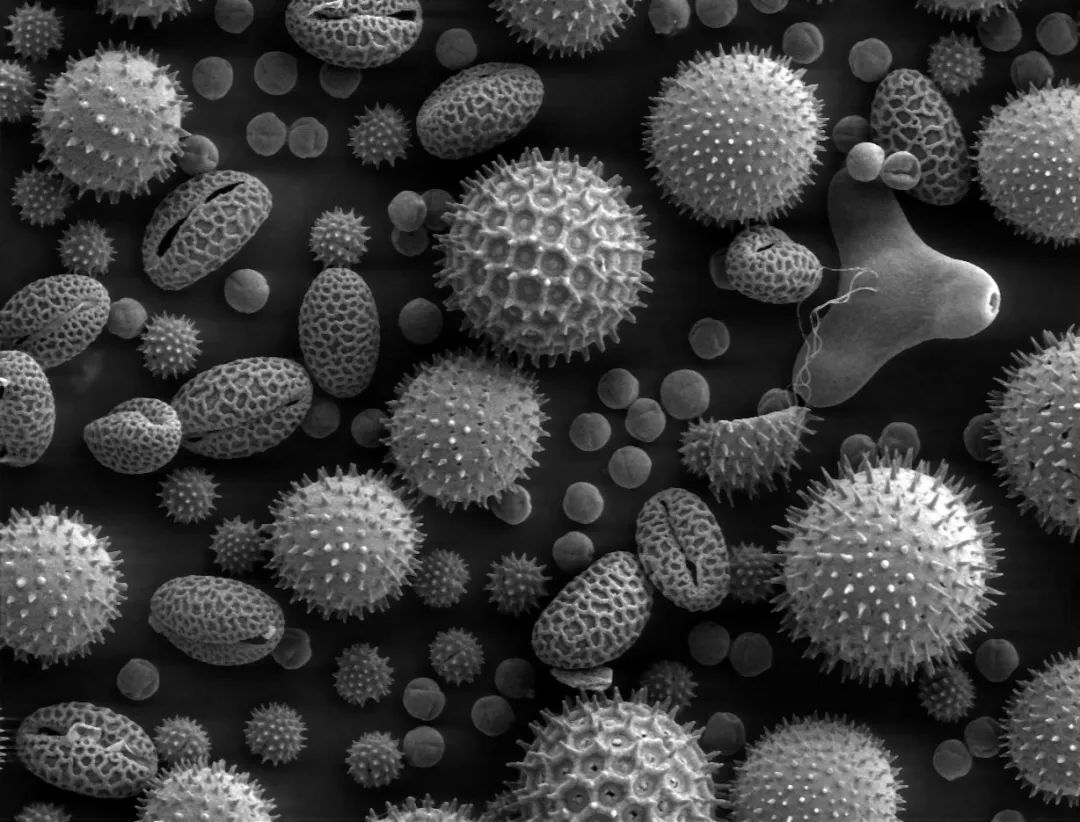
花粉具备足够大小，几乎无法观测到布朗运动 ｜ 图源 wiki

因为通常，花粉的直径分布在30～50μm之间，最小也有10μm左右。

而相比之下，水分子的直径大约为0.3nm（由于水分子非球形，具体尺寸依不同部位有所差异），大约是花粉直径的十万分之一。

因此，花粉很难产生不规则振动，事实上，花粉几乎不受布朗运动的影响。在罗伯特·布朗的手稿中，“tiny particles from the pollen grains of flowers”指的是“从花粉粒中迸出的微小粒子”，而非花粉本身。

然而在翻译成其他语言时，这一描述常常被误解，认为是“水中的花粉受布朗运动影响而呈现不规则运动”。

这种误解经过长期传播，已在大众观念中根深蒂固。

我们继续。

时光飞逝，来到了1905年。

这一年，年轻的阿尔伯特·爱因斯坦发表了一篇关于布朗运动的论文。

他提出，布朗运动是由于水分子不断撞击花粉粒引起的。爱因斯坦用数学公式描述了这种随机运动，揭示了布朗运动背后的物理原理。

爱因斯坦的公式可以简单地表示为：

其中：

- x^2 表示粒子位移的平均平方值。

- D 是扩散系数，描述了随机运动的强度。

- t  是时间。

3000步的2维布朗运动的模拟

通过这个公式，爱因斯坦展示了如何用数学描述随机过程，为布朗运动提供了一个科学解释。

与爱因斯坦同时期，波兰物理学家马里安·斯莫卢霍夫斯基也在研究布朗运动。他独立提出了类似的理论，通过统计力学的方法，进一步验证了爱因斯坦的理论。斯莫卢霍夫斯基的工作为扩散过程的数学描述增添了新的力量。

1914年，德国物理学家阿道夫·福克提出了一个描述布朗运动的微分方程，后来称为福克-普朗克方程。

这个方程为科学家提供了一个强大的工具，用于描述各种随机过程的时间演变。

1931年，苏联数学家安德烈·科尔莫戈罗夫对随机过程进行了系统的研究。

他提出了一组更加通用的方程，用于描述时间和状态空间中的随机过程。

这些方程后来被称为科尔莫戈罗夫前向方程（或福克-普朗克方程）和后向方程。

科尔莫戈罗夫前向方程描述了系统的概率密度函数随时间的演变，而后向方程则描述了条件概率的演变。这些方程为随机过程的数学描述提供了强大的工具。

那么它能干什么呢？

1、金融数学：预测市场波动

在金融市场中，股票价格、期权定价等问题可以用随机过程来描述。

布莱克-斯科尔斯模型（Black-Scholes Model）就是一个经典的例子，它用到了科尔莫戈罗夫方程来描述期权的定价。

通过这种方法，金融分析师可以更好地预测市场波动，制定投资策略。

2、生物学：解读自然现象

在生态学和生物学中，科尔莫戈罗夫方程用于描述种群的动态行为，例如动物的迁徙、扩散和繁殖。

生物学家用这个方程来研究不同物种在自然环境中的分布和变化，帮助我们理解生态系统的复杂性。

3、化学工程：优化反应过程

科尔莫戈罗夫方程在化学反应动力学中用于描述反应物和生成物浓度随时间的变化。

通过这个方程，工程师可以预测化学反应过程中的变化，优化反应条件，提高生产效率。

4、物理学：解析粒子运动

物理学家用科尔莫戈罗夫方程描述粒子扩散、热传导和流体力学等现象。通过这个方程，他们可以准确地预测粒子在不同环境下的运动方式，揭示自然界的运行规律。

5、神经科学：理解大脑运作

在神经科学中，科尔莫戈罗夫方程用于建模神经元的活动，描述神经脉冲的传递和扩散。通过这种模型，科学家可以更好地理解大脑如何处理信息，揭示神经疾病的成因。

6、环境科学：保护地球环境

环境科学家使用科尔莫戈罗夫方程描述污染物在空气、水和土壤中的扩散和传播。通过这个方程，他们可以预测污染物的传播路径和速度，制定环境保护策略，保护我们的地球。

7、工程与技术：设计高效系统

在控制工程中，科尔莫戈罗夫方程用于分析和设计控制系统，特别是那些涉及随机扰动的系统。通过这个方程，工程师可以设计出更加稳定和高效的控制系统，提升工业生产效率。

想象一下，有一个神奇的池塘，里面有很多小鱼。这些小鱼在池塘里游动，有时候会被水流推动，有时候会随机地游动。我们想知道，经过一段时间后，小鱼在池塘里的分布情况。

漂移：池塘里有一个温和的水流，推动小鱼向右游动。

扩散：小鱼有时候会随机地左右游动，没有特定的方向。

我们可以用科尔莫戈罗夫方程来预测小鱼的位置分布。

科尔莫戈罗夫方程可以写成：

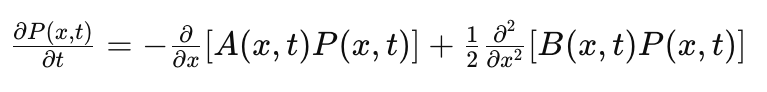
其中：

P(x,t) 是鱼在位置 x 和时间 t 的概率密度函数。

A(x,t) 是漂移系数，描述水流的速度。

B(x,t)是扩散系数，描述鱼的随机游动强度。

为了简单起见，我们假设：

水流的速度 A(x,t)=v 是一个常数。

鱼的随机游动强度 B(x,t)=D 也是一个常数。

因此，方程简化为：

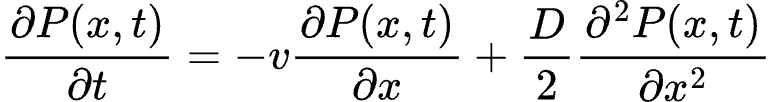
初始条件，假设在时间t = 0t=0 时，所有的鱼都集中在位置 x =0；

P(x,0) = δ(x)

以上可能会抽象，我们用写给程序来模拟，

import numpy as npimport matplotlib.pyplot as pltimport matplotlib.animation as animation# 参数设置num_particles = 1000  # 鱼的数量num_steps = 1000      # 总步数delta_t = 0.1         # 时间步长D = 1.0               # 扩散系数v = 0.5               # 漂移速度delta_x = np.sqrt(2 * D * delta_t)  # 每步的位移# 初始化位置数组x = np.zeros((num_particles, num_steps))# 生成随机游动轨迹for i in range(1, num_steps):theta = np.random.uniform(0, 2*np.pi, num_particles)x[:, i] = x[:, i-1] + v * delta_t + delta_x * np.random.randn(num_particles)# 创建动画fig, ax = plt.subplots()ax.set_xlim(-50, 50)ax.set_ylim(0, 0.1)line, = ax.plot([], [], lw=2)# 初始化函数def init():line.set_data([], [])return line,# 更新函数def update(frame):n, bins, patches = plt.hist(x[:, frame], bins=50, density=True, alpha=0.75)line.set_data((bins[:-1] + bins[1:]) / 2, n)return line,# 创建动画对象ani = animation.FuncAnimation(fig, update, frames=num_steps, init_func=init, blit=True, interval=30)# 显示动画plt.show()

运行如下：

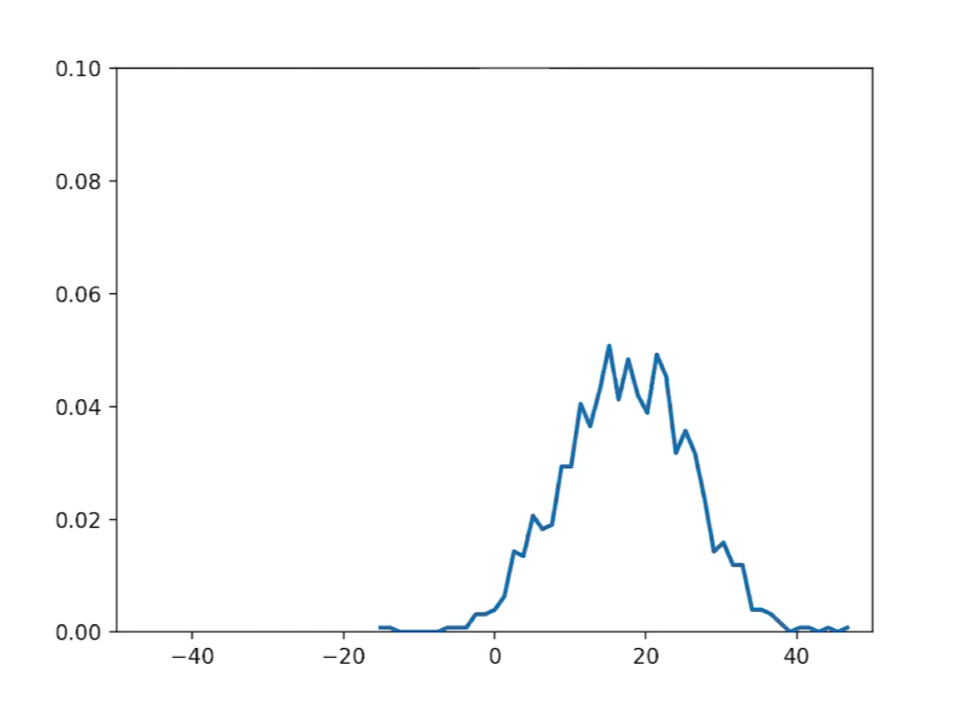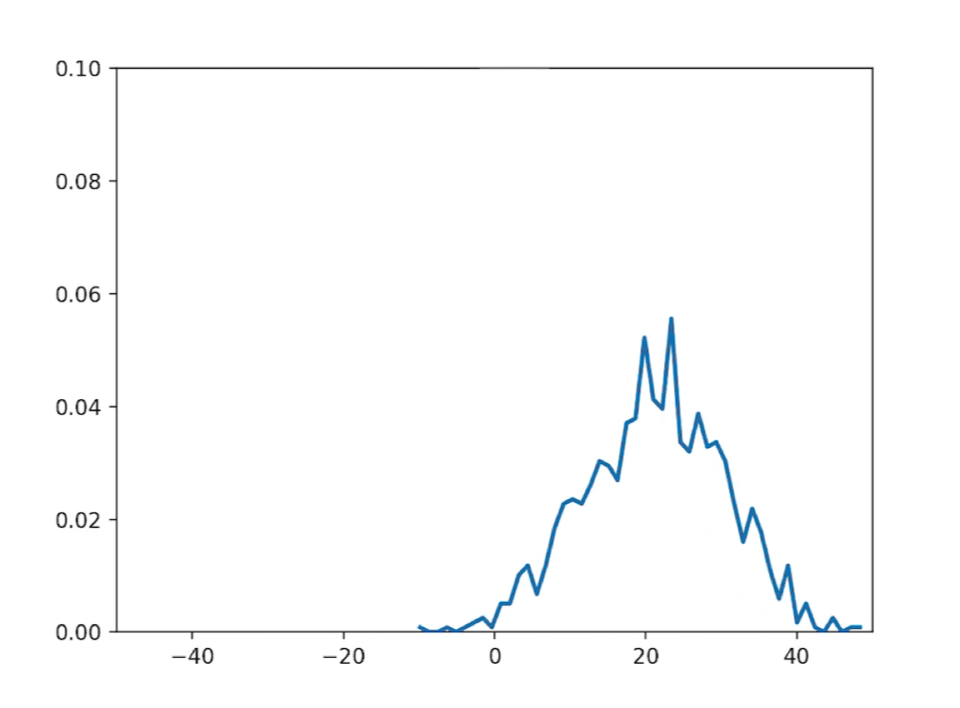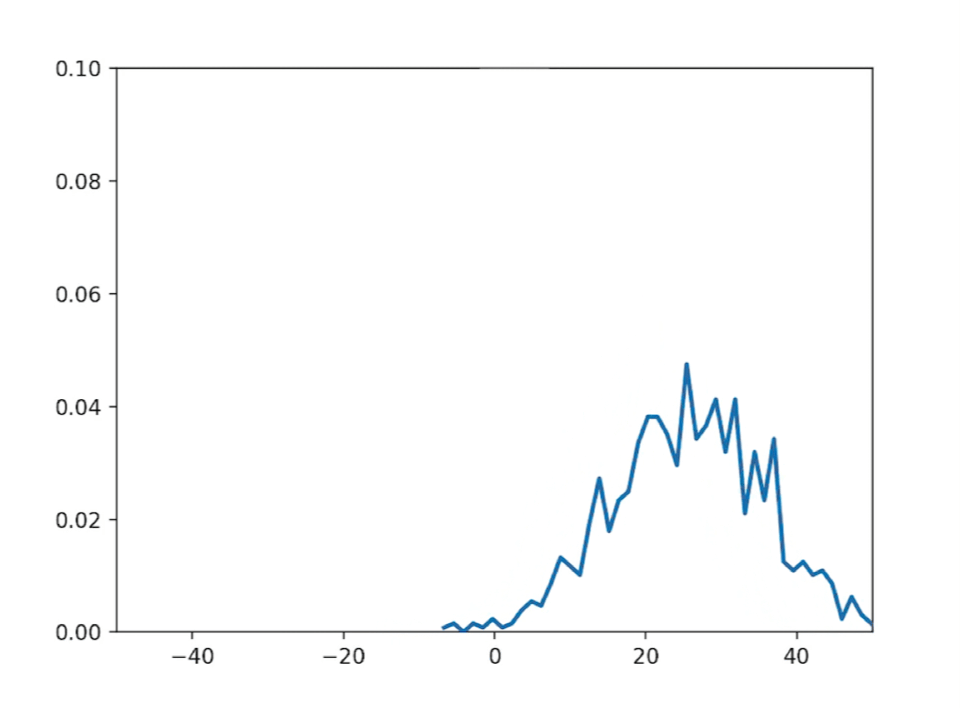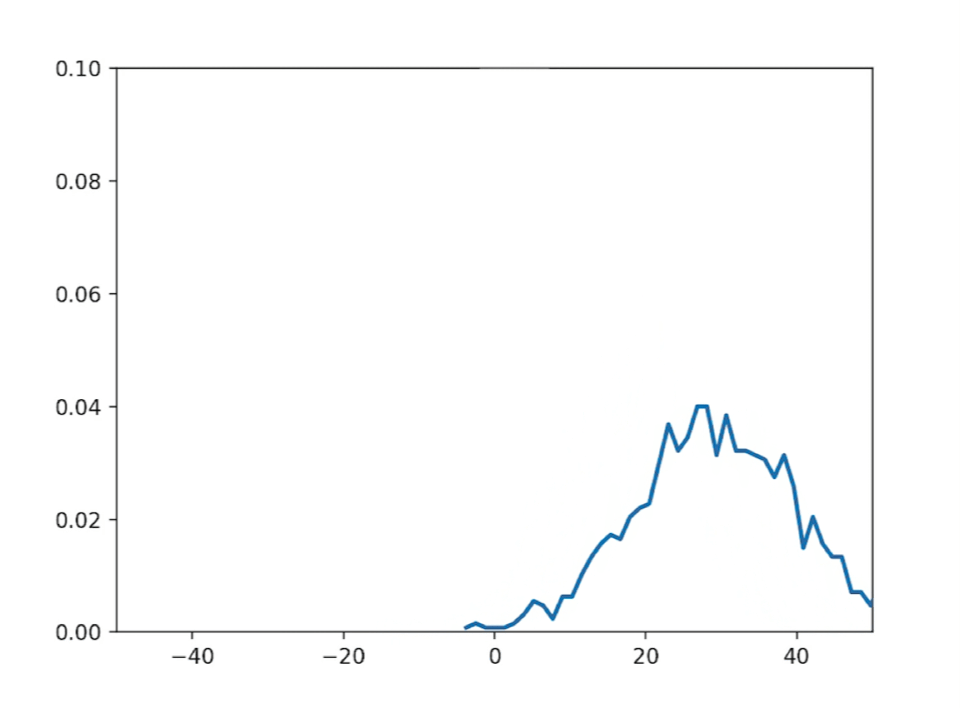
科尔莫戈罗夫方程的演变过程展示了科学家们对随机现象的深入研究和理解。

从布朗发现花粉粒的随机运动，到爱因斯坦和斯莫卢霍夫斯基的理论解释，再到福克和普朗克的方程推导，最终由科尔莫戈罗夫统一了这些成果，形成了我们今天所知的科尔莫戈罗夫方程。

这一数学工具不仅在物理学中有重要应用，还在金融学、生物学、化学工程、神经科学、环境科学和工程技术等领域发挥着关键作用。

通过理解和应用科尔莫戈罗夫方程，我们能够更好地应对实际中的各种复杂问题，揭示自然界的奥秘。