这篇文章，我们将探索微积分中一个极为重要的概念——格林定理（Green's Theorem）。这个定理将揭示如何将双重积分与线性积分联系起来。

无论你是刚开始学习积分，还是已经对线积分有所了解，这篇都会带你一步步深入理解格林定理的奥秘。我将用简单的语言和直观的例子，揭示这些数学概念背后的逻辑和美感。

让我们设想一个场景，在这个场景中，存在一个被我称为“F”的二维向量场。

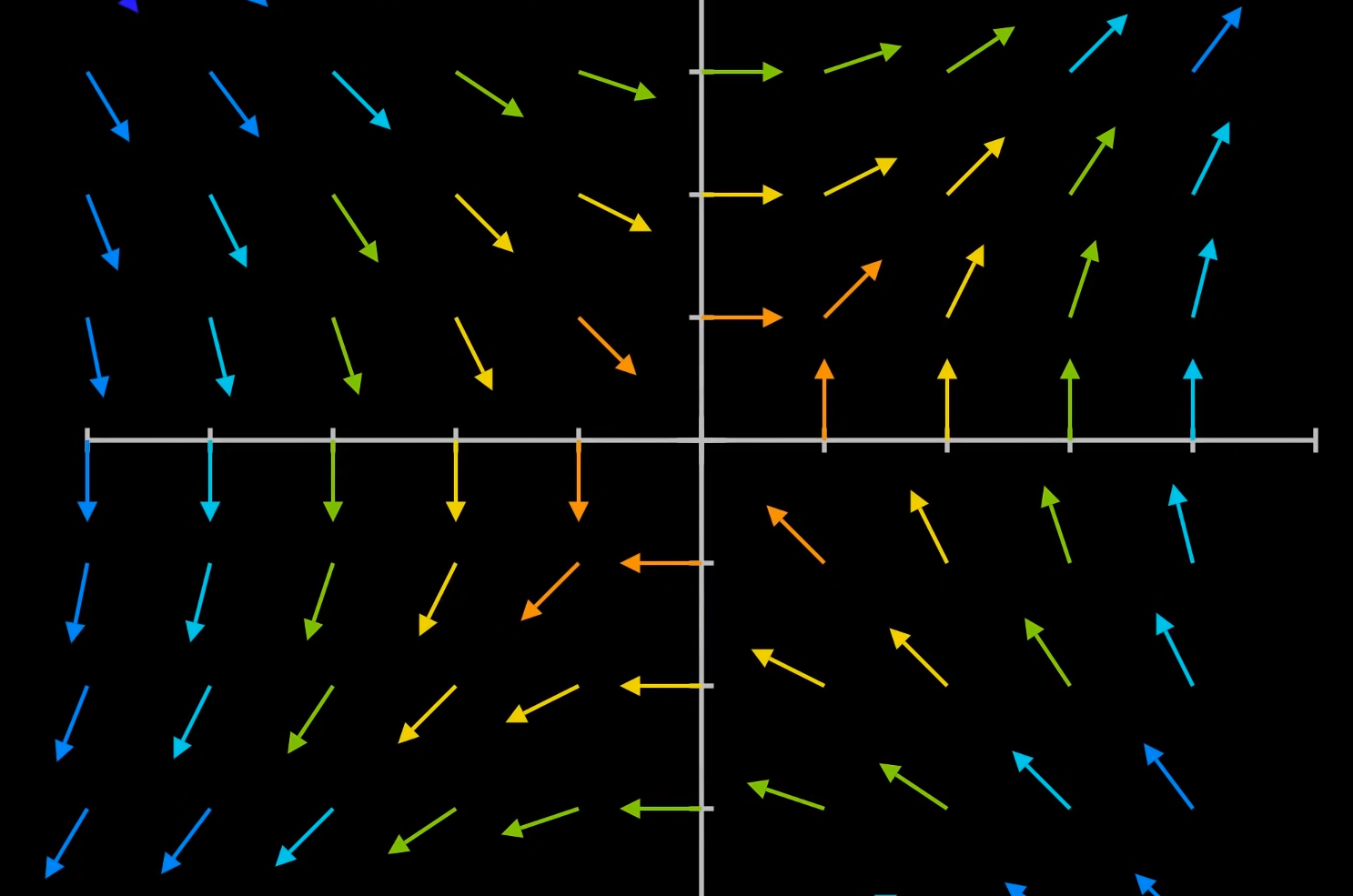
要理解这个向量场的概念，你可以想象在一个平面上的每个点上都放置了一个向量。这些向量代表了不同的方向和大小，形成了一个完整的向量场。在解释这个向量场时，我会使用不同的颜色来表示向量的大小（场的强度），因为如果用长度来表示，图形会显得过于复杂。

接下来，我们看下线积分，这涉及到一种特殊的曲线，我将这条曲线称为“C”。

在线积分的计算中，会沿着这条曲线计算函数的积分值，这是理解我们接下来讨论的内容的一个关键点。

这条曲线需要满足一些特定的条件。首先，这样的曲线应该形成一个闭合的环，意味着曲线的终点要回到其起点，从而构成一个循环。其次，这个闭合曲线应当按照逆时针方向绘制，逆时针方向为正。对于被这条曲线所包围的区域，我将简单地称它为区域R。

格林定理指出，在一个二维向量场中，我们可以通过计算围绕某区域边缘的封闭曲线上的线积分，来得到这个区域内向量场旋度（curl）的总和。

什么是旋度？

旋度是一个用于描述向量场旋转方向的量。在二维向量场中，如果旋度为正，这意味着向量场在该区域呈逆时针方向旋转；相反，如果旋度为负，则表示向量场在该区域呈顺时针方向旋转。值得注意的是，向量场即使在外观上不呈圆形，也可能具有非零的旋度。

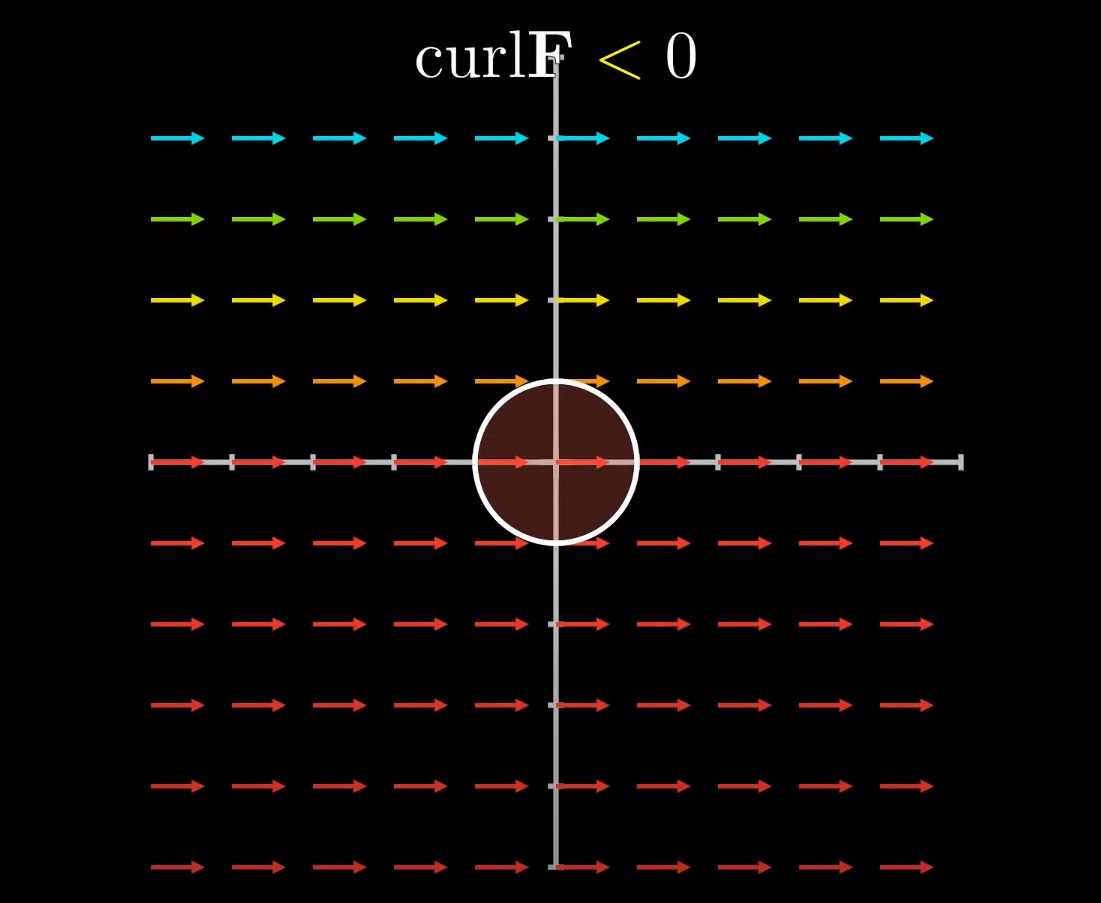
例如，假设一个区域的下半部分有更强的向量（幅值较大），而上半部分的向量较弱（幅值较小），这种分布可能会产生整体的逆时针旋转，即正旋度。数学上，旋度可以通过计算Del向量（一个涵盖所有偏导数的向量）与向量场的叉积来表示，这反映了向量场在不同方向的变化率。

这里有一个重要的点。如果区域R的整体旋转是逆时针的，那么线积分将是正的，如果整体旋转是顺时针的，那么线积分就是负的。如果将线积分分成两条曲线会怎样？

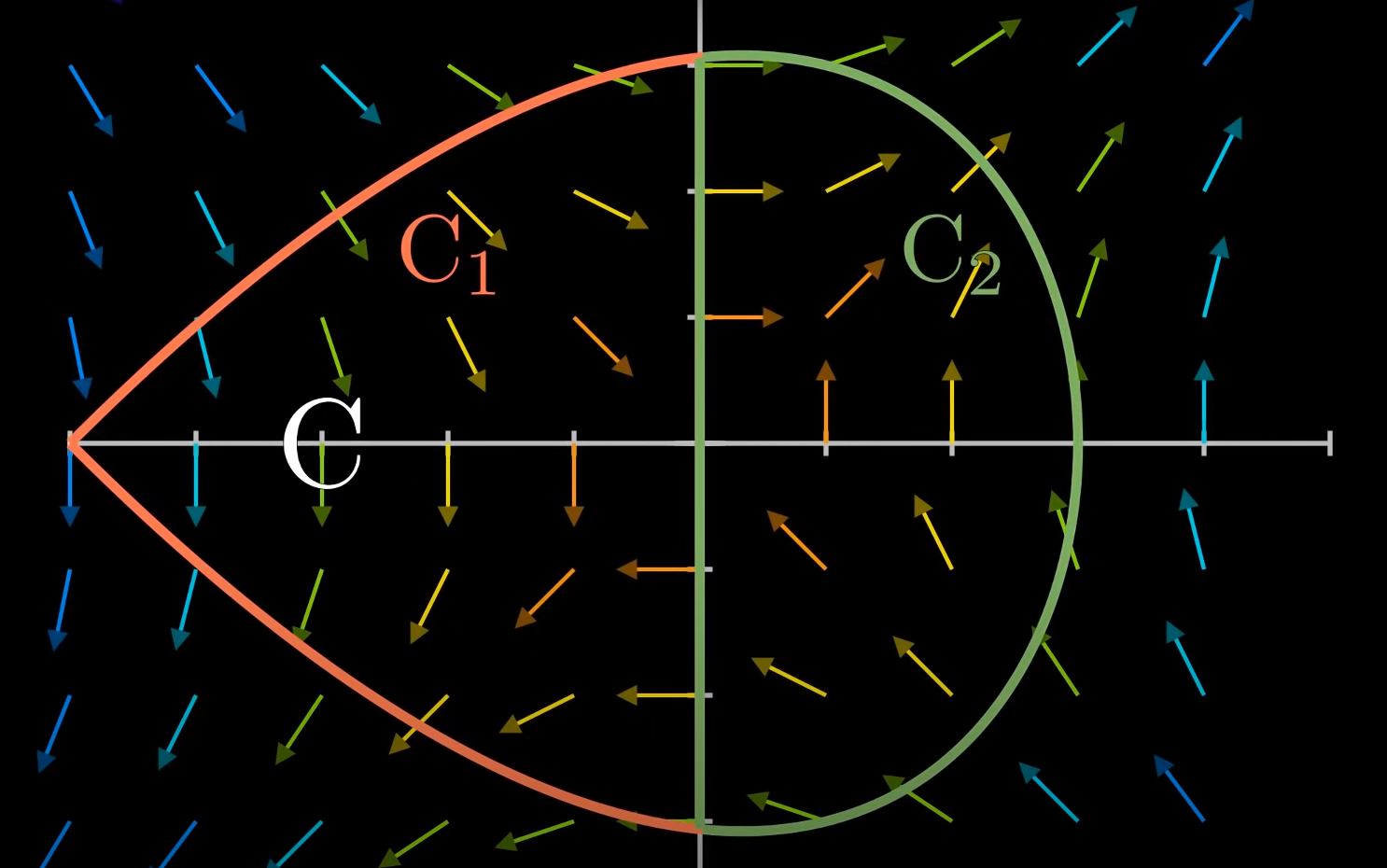
得到的积分是F在c1上的线积分加上F在c2上的线积分，

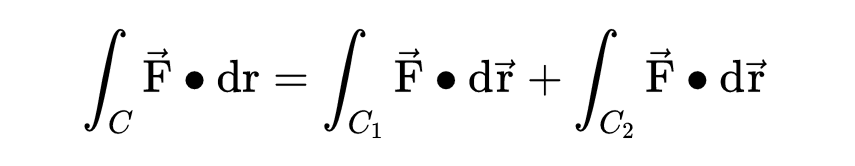
这和在C上的线积分是一样的！这是因为中间的线被抵消了。一个是从上到下，另一个是从下到上。这是一个非常重要的事实。它意味着我们可以将曲线分成任意数量的曲线。

现在，让我们将大的区域分成许多许多小区域。

一种描述向量场旋转度的方法是旋度！旋度是针对向量场中的点。因此，我们可以通过计算每个点的旋度，并将其乘以该点周围的一个小面积区域，来估算线积分的值。这种方法适用于向量场中的每一个点，通过对整个区域内所有这样的小区域进行相同的计算并累加结果，我们可以得到整个区域线积分的近似值。简而言之，通过分析向量场中每个小区域的局部旋转，我们可以估算出整个区域的线积分，就是双重积分，

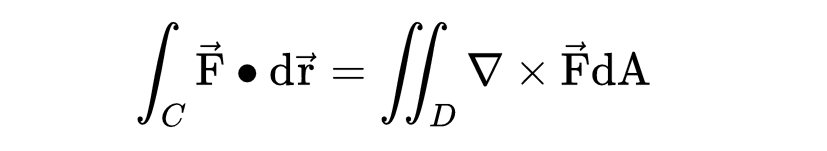
在微积分中，我们总是使用这种无限逼近的概念。

例如，在学习定积分时，我们采用了类似的方法。通过使用黎曼和的概念，我们可以近似计算出曲线下的面积。这种方法涉及到将区域划分成若干小矩形，并计算每个矩形下的面积。随着矩形数量的增加，这些小矩形的面积之和越来越接近曲线下真实的面积。

之前，我们确定了可以将一条曲线分割成任意多个部分，并计算每个部分上的线积分，以此来得到整条曲线的线积分。从微积分的角度来看，可以观察到，当我们使用大量更多的矩形时会发生什么。

随着矩形大小趋近于零，向量场的旋度成为对每个小部分的线积分更好的近似。因此，我们可以将区域R内每个点的旋度相加，以得到整条曲线的线积分。

现在我们有了向量场上的线积分，可以描述为同一向量场的旋度的双重积分。双重积分与曲线所围成的内部区域有关，并且可以仅通过观察边缘来确定。这与单变量微积分中的基本定理相似，其中曲线下的面积可以通过观察端点来确定。

现在让我们看一个例子。假设有一个向量场

曲线C是，

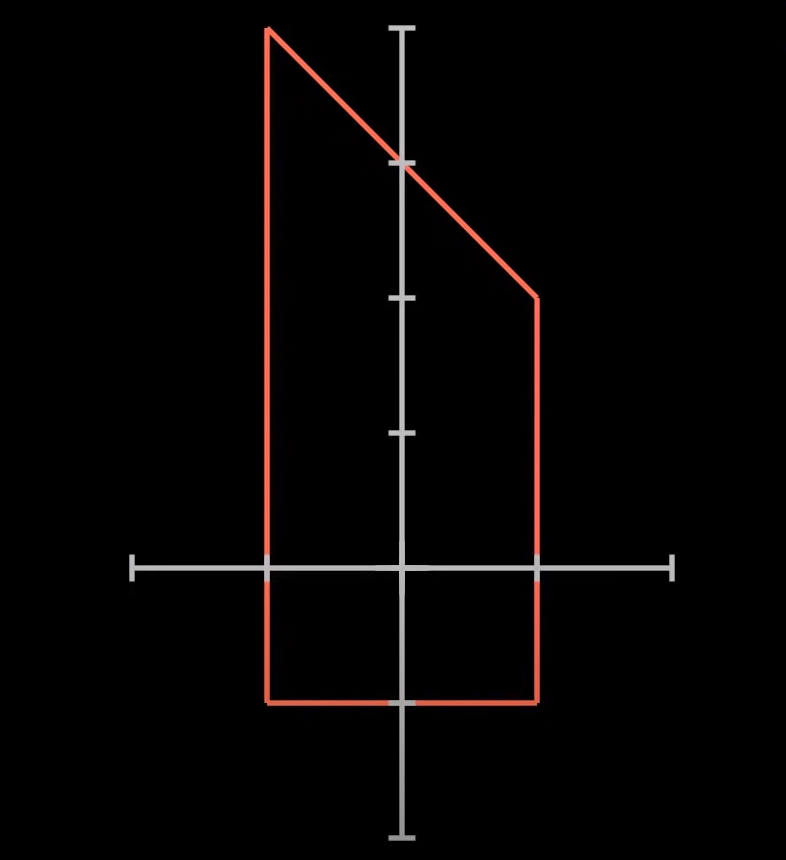
让我们尝试计算F在C上的线积分。

格林定理指出，这个向量场在C上的线积分等于二维旋度在该区域内的双重积分。所以首先，让我们计算向量场的二维旋度。这等于x-9，

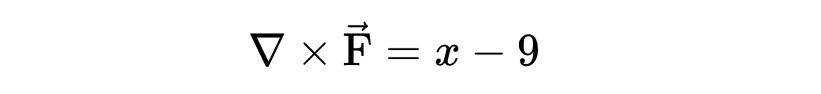
现在要计算这个线积分，需要计算x-9在R上的双重积分。上线是y = 3-x，下线是y = -1。x的范围是 -1到1。所以双重积分等于

得到-218/3。

格林定理展示了数学在描述自然现象和物理法则方面的深刻性。它被视为展示微积分美妙结构的一个例证。在数学教育中，格林定理是多变量微积分核心课程的一部分。它不仅教会学生们具体的计算技巧，还启发他们理解数学概念的深层含义。