关于太阳、地球和月球，一种常见的描述就是：地球是太阳的行星，它一直在围绕着太阳公转，月球是地球的卫星，它一直在跟着地球。据此我们似乎可以认为，地球对月球的引力应该比太阳更大，然而实际情况却并非如此，这可以通过简单的计算来进行说明。

根据万有引力定律，两个天体之间的引力可以用公式“F = Gm1m2/r^2”来进行计算，其中G是万有引力常数，m1、m2分别是两个天体的质量，r是它们之间的距离，已知：

太阳的质量约为1.989 x 10^30千克

地球的质量约为5.965 x 10^24千克

月球的质量约为7.349 x 10^22千克

日地平均距离约为1.496 x 10^11米

地月平均距离约为3.844 x 10^8米

月球和太阳的平均距离可以粗略地认为与日地平均距离差不多，引力常数可取值为6.67 x 10^-11。

将这些数据代入引力计算公式可得，太阳和地球对月球的引力分别约为4.36 x 10^20牛顿、1.99 x 10^20牛顿，也就是说，太阳对月球的引力比地球大了两倍有余（约2.2倍）。

这样的情况就有点令人困惑，既然如此，月球就应该被太阳的引力“吸”过去，那为什么月球会一直跟着地球呢？其实这是可以解释的，答案就是：对于月球而言，太阳和地球对它的引力并不是想象中那样的“拔河比赛”，而是各有各的作用。

对于太阳来讲，地球和月球其实都在围绕着它公转，在此过程中，太阳的引力不仅作用于月球，还作用于地球，其实是起到了向心力的作用，而在地月系统中，月球一直在围绕着地球公转，地球对月球的引力，同样也是起到了向心力的作用。

所以我们可以将月球的运行状态简单地理解为：月球其实一直在围绕着太阳公转，只不过在地球引力的束缚下，它在围绕太阳公转的同时，也在围绕着地球公转。

（上图为按照实际比例绘制的地月系统围绕太阳运行的轨迹，可以看到，在这个比例上，地球的引力对月球运行轨道的影响其实是非常小的）

由于引力的大小与距离的平方成反比，因此当距离超过到一个临界值的时候，地球的引力就不能对月球形成有效的束缚。

所以我们可以简单地认为，以地球为中心，以这个临界值为半径的球体空间，就是地球的“势力范围”，只要月球运行在这个范围之内，它就可以稳定地做到“在围绕太阳公转的同时，也围绕着地球公转”。

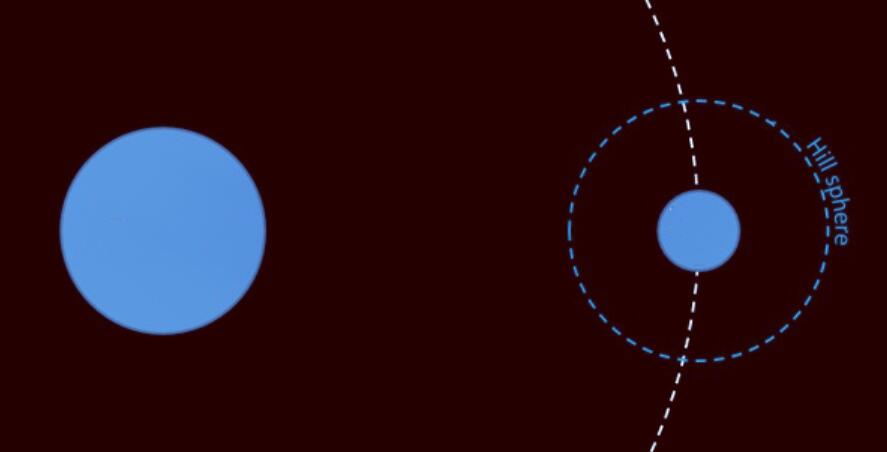
实际上，在天体物理学中，这个“势力范围”有一个专用的名称——“希尔球”（Hill sphere），简单来讲，“希尔球”就是指当一颗行星在围绕主恒星运转时，行星的引力对其卫星形成有效束缚的最大距离范围。

需要注意的是，这并不是说在“希尔球”之内，行星对卫星的引力就比主恒星更大，而只是说在此范围之内，行星对卫星的控制力相对于距离更远的主恒星更强。从理论上来讲，“希尔球”可以通过这样一个公式来进行描述：

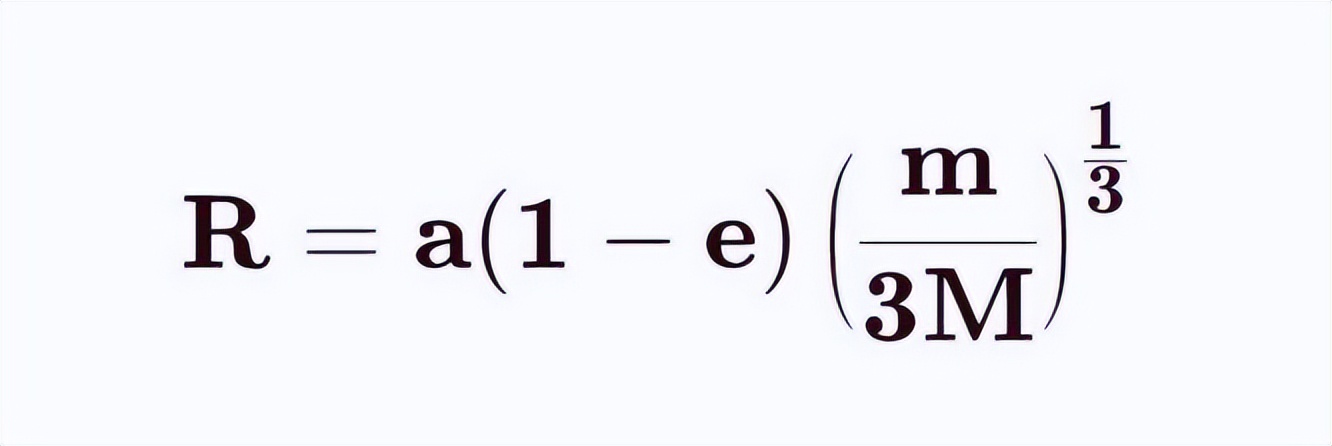
其中R是行星“希尔球”的半径，a是行星围绕主恒星的轨道半长轴，e是行星的轨道偏心率，m是行星的质量，M是主恒星的质量。

地球围绕太阳的轨道半长轴可取值为1.496 x 10^11米，轨道偏心率可取值为0.0167086，太阳和地球的质量前文已经给出了，我们将这些数据代入这个公式，就可以计算出，地球的“希尔球”半径大约为150万公里。

也就是说，只要月球围绕地球的公转轨道位于以地球为中心、半径为150万公里的球体空间之内，它就可以一直稳定地围绕着地球公转。

观测数据表明，在月球围绕地球的公转过程中，它与地球的平均距离约为38.4万公里，最远距离（也就是“远地点”）也只有大约40.5万公里，可以看到，这远远地低于150万公里的理论值，所以月球当然就会一直跟着地球。

值得一提的是，在太阳系的八大行星之中，水星的质量最小，距离太阳最近，因此水星的“希尔球”半径是最小的，大约只有17.5万公里，而海王星的质量虽然不是最大的，但是它距离太阳最远，以至于它的“希尔球”半径达到了大约1.16亿公里，并因此成为了太阳系中“希尔球”半径最大的行星。