英国数学家霍奇（William Vallance Douglas Hodge）于1950年提出的霍奇猜想，无疑是所有千禧难题中最难理解的。这是个高度专业的问题，只有极少数专业数学家才能真正地理解。下面是霍奇猜想：

一个非奇异射影代数簇上的每一个（一定类型的）调和微分形式都是代数闭链的上同调类的一个有理组合。

是不是发现，这个句子中的每一个专业术语你都不理解。在关于伯奇和斯温纳顿一戴尔猜想的文章中，我还可以把那个猜想与简单的几何联系起来，即三角形面积问题。

对于霍奇猜想，甚至想找些简单的类比都没有。霍奇猜想最清楚地说明了，现代数学的本质使它的大部分几乎不可能被普通人所领会。

一个世纪以来，数学家在旧的抽象上面建立了新的抽象，与其说数学家做出了新东西，不如说被考虑的对象变得更为抽象了。以霍奇猜想为例，微积分的运算在这里扮演了一个主要的角色，但是这个微积分不是像许多高中生所学到的那样在实数上进行，甚至也不在复数上进行。这是在更一般、更抽象的背景上进行的微积分。

对普通人来说，这个问题的难以理解正是它最有趣的地方。话虽如此，但我还是想试图解释一下霍奇猜想说的是什么。

17世纪，法国哲学家笛卡儿把几何代数化，把几何图形放在笛卡尔坐标系中，然后建立它们的数学方程。用代数来研究的几何通常称作代数几何，也叫笛卡儿几何。

19世纪期间，数学家将笛卡儿的方法向前推进了一步。他们不是只把代数当作一种工具，来研究几何对象，而是从代数方程着手，把这些方程的解定义为"几何"对象。但是大多数方程并不对应着我们熟悉的几何对象。因此称它们为"几何对象"是讲不通的。以这种方式，从代数方程产生的对象，数学家所给的名称是“代数簇”。

在定义代数簇时，数学家并不是仅考虑一个代数方程，而是一个方程组（有限个）。在由两个方程组成的方程组中，每一个方程定义了一个几何图形，那么由这个方程组定义的簇将是这两个图形的共有部分。）

因此，代数簇是几何对象的一种推广。任何一个几何对象都是一个代数簇，但是有许多代数簇是不可能被可视的。然而，并不因为某个特定的代数簇不可能被可视化，我们就无法研究它。

现在，我们可以看一下霍奇猜想中的一个专业术语∶一个非奇异射影代数簇，简单说，就是一个光滑的多维"曲面"，它由一个代数方程的解所产生。这就像一个球面是通过解代数方程

而得到的一个光滑的二维曲面。

这个猜想针对那种“曲面”上的“调和微分形式”作出了一个断言。一个调和微分形式是某个十分重要的偏微分方程（称为拉普拉斯方程）的一个解，它既产生于物理学，也产生于复变函数的研究。

大学学习的微积分通常是在二维平面上。但是小小地努力一下，就可以把它推广到其他曲面上，例如球面上。再努力一下，就可以把微积分推广到各种各样更为一般的簇上。霍奇猜想涉及的是推广到一个非奇异射影代数簇上的微积分。它对某种类型的抽象对象作出了一个断言，我们把这种抽象对象称为H对象，如果我们从某种类型的簇着手并在其上做某种微积分，就会产生H对象。

当我们用微积分去定义一个对象时，定义出来的对象从任何意义上说都不一定是"几何的"。霍奇猜想说，H对象对刚才这句话来说是个例外。虽然它们本身可能不是几何对象，但它们能以一种相当简单的方式由几何对象构建起来。在这个猜想的术语中，H对象就是代数闭链的上同调类的一个有理组合。这就是说，任何H对象都能以一种纯粹代数的方式由几何对象构建起来。

因此，你可以认为霍奇猜想是说∶

通过在簇上运用微积分，我们创造了一类对象（H对象），这类对象不仅让我们想把它们可视化的希望成为泡影，甚至让我们不能用代数方式描述它们。然而，这些对象能以一种代数的方式，由“能用代数描述的对象”建造起来。

霍奇猜想的作用是给专家们提供某种能用来分析H对象的强有力的数学结构。这在许多现代数学中十分重要，数学家不断在寻找对象上的新结构，或者是寻找从一个领域到另一个领域的联系，以使他们能把来自一个领域的方法加以改造，运用于另一个领域。

现在，我们对霍奇猜想有了一个整体的认识了。下面是另一种理解这个问题的方式。

我们可以从代数簇上沿着广义路径的积分着手来提出霍奇猜想。由于对路径进行变形仍能保持这种积分的值不变，因此你可以认为这种积分是定义在路径类上的。霍奇猜想提出，如果某些这样的积分为零，那么在这个路径类中存在着一条能用多项式方程描述的路径。

这里先吹一下霍奇猜想的重要意义：霍奇猜想的证明将在代数几何、分析和拓扑学这三个学科之间建立起一种基本的联系。

直到现在，霍奇猜想仍然只是一个猜想。1991年，美国数学学会出版了一本书，书中记载了人们对霍奇猜想已做的一些研究，列出了发表于1950年至1996年的71篇论文，这些论文都仅仅是关于这个猜想的一个方面，即所谓的阿贝尔簇上的霍奇猜想。

下面是这本美国数学学会的书在其序言的开头一段对霍奇猜想的陈述，

对于霍奇（William Hodge）这样一位如此优秀的数学家，人们对他几乎一无所知。他1903年出生于苏格兰的爱丁堡。他先是在爱丁堡，然后又在剑桥完成了学业。1936年，33岁的他被剑桥大学委任为教授，直到1970年退休。

他是开发几何、分析和拓扑学之间联系的一位主要人物。数学家如今还记得他主要是因为（除了他的猜想之外）他的调和积分理论。

1938年，他入选伦敦的皇家学会，于1957年被授予皇家奖章，以表彰他在代数几何上的杰出贡献。从1947年到1949年，他任伦敦数学会会长，并于1952年获得这个学会的贝里克奖。1974年，皇家学会再次奖励他，这次是授予他科普利奖章，以嘉奖他在代数几何上的开创性工作，特别是他的调和积分理论。霍奇于1975年逝世，享年72岁。

在职业生涯的大部分时间里，霍奇都致力于发展代数几何理论，其中的一个理论现在就称为“霍奇理论”。他的猜想就是产生于代数几何。1950年在英国剑桥举行的国际数学家大会上，霍奇在他的演讲中宣布了这个猜想。

文艺复兴时期，数学家谈论一件不可思议的事∶在代数中引进一个数，它的平方是-1。这个数用i表示，成了复数的基础。

虽然人类很难接受一个数的平方为负，然而复数具有一套有效的算术运算，就像通常的实数算术运算一样，而且我们还可以求解包含复数的多项式方程。克服复数反直觉的方法是认识到它们可以作为“点”在普通的二维平面上画出来。

实数中，我们可以把每一个实数r与它的相反数-r相对应。画在一条直线上（“实数线”），每个数由位于原点另一侧且与原点有同样距离的点与之配对。这种特定的配对在实数的算术运算中起到了重要的作用。

复数可以作为复平面上的点被画出。对于这些数，取x＋iy与-x-iy对应的类似配对是一种关于原点的反射。但是复数有另一种配对，它在复数的算术运算中起到了重要作用。第二种配对是把每个复数x＋iy与它的共轭复数x-iy对应。复数共轭配对是关于复平面上实数轴（即x轴）的反射。

到19世纪，复数的基本理论已被成功地研究出来，复数被普遍认为是主流数学的标准数系。而且，数学家开始发展一种把微积分推广到复变函数的理论，从而产生了复分析。

复分析早期研究的两位主要人物是黎曼和柯西。他们把复变函数与物理学联系了起来。他们开始于这样的思考∶

如果f（z）是复变量z的一个复值函数，那么我们可以把这个函数的f（z）值写成f（z）=u（z）＋iv（z）的形式，其中u（z）和v（z）都是实数。这就给出了两个新的函数u和v，它们都是复变量z的实值函数。

这两位数学家发现，如果复变函数f有着定义良好的（微积分）导数（用现代的术语，如果函数f是解析的），那么它的实部u和虚部v必须满足两个偏微分方程：

这些方程对物理学家来说是很熟悉的。它们是拉普拉斯方程，在引力理论、电磁理论和流体力学中起着重要作用。拉普拉斯方程的一个解被称为调和函数。复变函数的微积分和拉普拉斯方程之间紧密联系的发现，导致了数学物理学的重大进步。

复变函数理论中的一个重大进展是黎曼曲面的发明。有一些函数，它们对实数很友好，但是当自变量或者函数值允许是复数时，结果完全不像是一个正常的函数，因为一个自变量可以导出不止一个的函数值。平方根函数和对数就是两个例子。

对于实数来说，任何一个正实数都有两个平方根，但由于其中一个为正，另一个为负，所以只要规定取正根，问题就能排除。但是当这个根是复数时，没有一种自然而有效的方法在两个根当中作出选择。黎曼提出，处理这些“多值函数”（它们根本不是真正的函数）的最好方式是把它们看作定义在一个多层曲面上的单值函数（即真正的函数）。

黎曼曲面有着比复平面更为复杂的拓扑结构。看待它们的一种方式是把它们当作复平面的一种螺旋梯式构形。

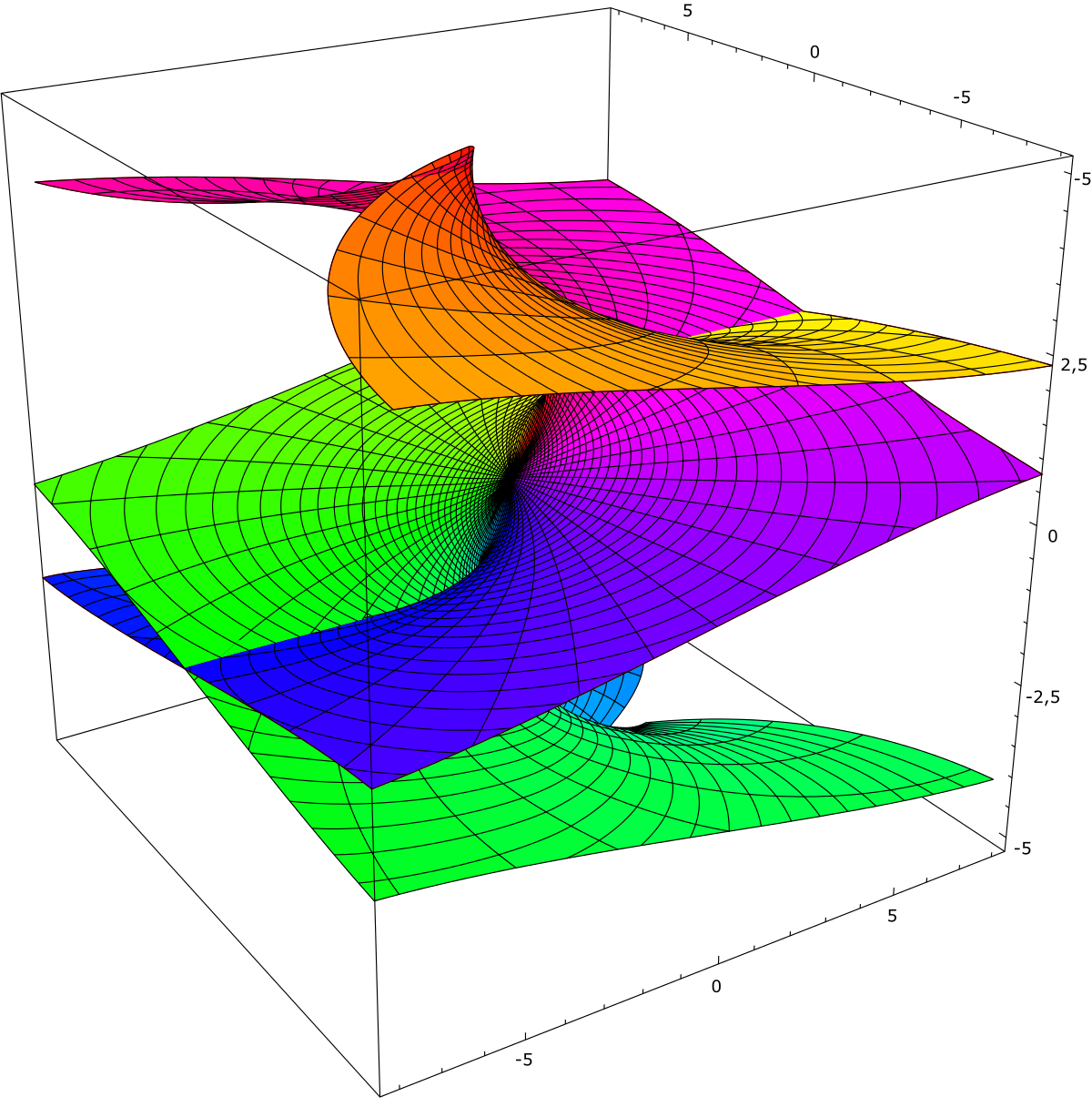
20世纪早期，数学家把黎曼曲面的思想推广成一个高度抽象的概念——复流形，即黎曼曲面的一个有着一种复杂拓扑结构的多维模拟物。这样一个流形具备了一种能确保复解析函数的概念有意义的结构。特别是，有可能定义所谓的微分形式，即把通常（实数）微积分中函数f的微分df推广到多维情况的产物。

有些微分形式可以分成具有某种共同关键特征的不同类型，所以它们被称作上同调类。这些上同调类正是霍奇猜想所说到的。

要理解上同调类的概念需要一系列高深的专业数学知识。下面是一个十分简要的概括∶

首先，我们需要知道在微分形式上存在着一种特定的运算，称作外导数。外微分本身就是一种微分。

如果一个微分形式是另外某个微分形式的外导数就称这个微分形式是恰当的。

如果一个微分形式本身的外导数是零，就称这个微分形式是闭的。

如果两个闭微分形式的差是恰当的，就称它们是上同调的。

因此，上同调类的元素是闭微分形式。恰当性是同一上同调类中的元素共有的“相似性”性质。注意上同调类的定义十分依赖于来自微积分的概念。

上同调类定义了有用的拓扑不变量，它们抓住了基本复流形的重要方面。获得了（闭微分形式的）上同调类概念，我们就可以回到代数几何和代数簇概念。一个复代数簇是由一个代数方程组的复数解所定义的一个多维“曲面”。

如果定义一个复代数簇的方程组的解仅依赖于有关数的比，数学家就称这个复代数簇是射影的。

如果一个簇作为“曲面”是光滑的，他们就称这个簇是非奇异的。

因此，一个非奇异射影复代数簇就是一种特殊类型的复流形。

霍奇意识到他可以把来自于分析的方法应用于这些代数流形。特别是，他意识到由一个非奇异射影复代数簇所产生的微分形式的有理上同调类可以被看作是拉普拉斯方程的解。

霍奇的观察结果使得有可能把这样的一个类写成一些特殊分量的一个和，这种特殊分量称作调和（p，q）形式。它们是可以由p个复变量和q个共轭复变量所规定的拉普拉斯方程的解。而且，每个（p维的）代数上同调类给出了一个（p，p）形式。

霍奇在他对1950年国际数学家大会所作的报告中提出，对于非奇异射影复代数簇，上面说到的最后那个性质可能完全刻画了代数上同调类。也就是说，每个调和（p，p）形式是闭代数形式的一个有理组合（概略地说，即它可以用一种代数的——即不用到微积分的——方法构建起来）。

霍奇猜想就是这样诞生的。但是这个猜想是否正确？无人知晓。