在数学中，对角论证常被用来证明某一对象不存在。要把这一论点准确地形式化是比较困难的，但通过看一些例子就很容易理解了。

康托尔的对角论证

第一个用对角论证的人是乔治·康托尔。他指出在无穷个0和1的序列（二元序列）和自然数之间不存在双射。换句话说，我们没有办法枚举所有的二元序列。你可能不相信他，那你可以自己试着枚举，把每一个“二元无限序列”一行一行地写下来，如下图：

然后取对角线。我们构造一个新的序列，方法如下：

取上图的对角线数字（上图红色的数字）。

将对角线数字作取反运算，即把“0”变为“1”，把“1”变为0。

得到如下序列s：

这个枚举“s”的索引下标为i，即s变成了s_i。现在问题来了，s_i[i]是什么？即序列s_i中的第i项是什么？

如果s_i[i]是0，那么根据s的生成规则，s[i]变为1。但是根据我们的假设，s[i] = s_i[i]，因此s_i[i] = 1。

如果s_i[i]是1，那么根据规则，s[i]变为0。但由于s_i[i] = s[i]，因此s_i[i] = 0。

这产生了矛盾。不要轻易质疑康托尔。

红色方块不能被定义，因此水平放置是不可能的

这就是康托如何证明存在一个比“可数的无穷大（自然数）”更大的无穷大（无限二元序列的集合）。现在我们要证明对于每一个无穷大存在一个更大的无穷大。

正式地，我们将证明对于任何集合X，在X和X的所有子集之间不存在双射。再次假设这种双射存在，并将其命名为e，然后定义：

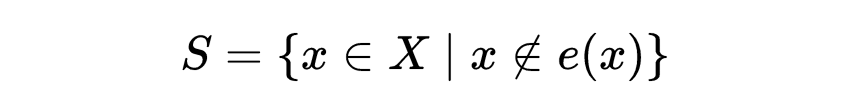
显然，S是X的子集，所以对于X中的某个x，S = e(X)。现在，我们再次思考X是否在S中，并发现在任何情况下都存在矛盾：

若x∈S，则根据定义x ∉ e(x) = S，

若x ∉ S，根据定义，x∈e(x) = S。

所以这样的双射不存在。

这个论证有点难理解，因为我们对整个过程没有一个清晰的印象。但这就是对角论证的要点。这很困难，因为它以一种矛盾的方式使用自己。

罗素悖论

罗素悖论也始于康托，他试图引入一个新概念，这个概念在数学中已经不可或缺。一个我们已经用过的概念，集合。但这个概念有一些问题。伯特兰·罗素在1901年注意到，如果我们定义一个集合，它包含所有不包含自身的集合：

这里产生了矛盾。也就是说，我们不能回答R是否包含它自己（R ∈ R）的问题。

如果R包含它自己，那么根据R的定义，R不包含它自己。

如果R不包含它自己，那么根据定义，它应该包含它自己。

那么到底是什么导致了这里的矛盾的呢？要问R是否属于R，R必须是一个集合。所以挽救集合理论的方法就是不把R看成一个集合。事实证明，这是可行的。如果你想了解更多关于集合理论是如何形式化的，就需要了解ZFC公理，这是另一篇文章的内容了。

停机问题

1936年，艾伦·图灵证明了“停止问题”（Halting problem），即没有一种算法可以判定一个给定的程序是否终止（它的执行在有限的时间内结束）。这又是一个烧脑定理，它与对角论证有一定的联系。

假设有这样一个算法A，当在一对(X, Y)上运行时，决定算法X是否在其输入Y上运行终止。然后我们定义另一个算法B，给定输入W，执行以下操作：

如果A在(B, B)上运行返回True，那么B在B上停止，这只能发生在A在(B, B)上运行返回False时，

如果A在(B, B)上运行返回False，那么B不会在B上停止，这意味着A在(B, B)上运行返回True。

我们再次看到，在每一种情况下，都会产生矛盾。所以算法B不存在，也就是说算法A也不存在。

这可能很难理解。我们认为输入和算法是相同的。事实并非如此。形式上，我们将算法编码为输入字符串（它们的代码）。

哥德尔不完备定理

我不能不提到哥德尔的不完备定理。不完备定理是说

在基于大量公理的数学中，总是会有一个句子不能被证明。这个句子叫作哥德尔句子。

在同样的约束条件下，数学无法证明自己的一致性。所以它甚至不能证明自己是不矛盾的。

我省略了一些严格的数学细节来解释对角论证的作用，因为证明太复杂了。这里只能说明，对角论证在其中起到了作用。形式上，它意味着我们必须能够构建一个算法，告诉我们一个给定的公理是否在一组公理中。

对角论证在数学中有着广泛的应用，并建立了一些非常基本的定理。它以自我参照的方式来证明事情，会让你的思维扭曲，让你明白为什么你认为是真的东西是不可能的。