变分法是对已知的微积分进行扩展，将其应用于无限维空间，特别是函数空间。普通的微积分关注的是一个或多个实变量的函数，而变分法处理的是函数的函数，即泛函。本文的主要目的是证明，只要给出正确的导数定义，变分法与普通微积分非常相似。我将有限维和无限维优化问题进行比较，并揭示无限维问题可以使用有限维的思想来求解。我利用这些思想推导出著名的欧拉-拉格朗日方程（Euler-Lagrange equations）。

优化是数学、工程学、计算机科学等领域中寻找最佳解决方案的过程。优化的目标通常是在给定约束条件下，最大化或最小化某个目标函数。在实际应用中，优化问题可以涉及到不同领域的诸多问题，如资源分配、生产调度、投资组合选择、机器学习模型调整等。

最简单的形式是，优化问题作为一个函数给出，我们寻求使这个函数达到最小值或最大值的点。

以金融领域的马科维茨投资组合（Markowitz Portfolio）为例。假设我持有两种风险证券，其收益率方差分别为σ₁和σ₂。它们的协方差是c。我应该持有多少比例的每种证券以使投资组合的方差最小？

假设投资组合中第一种证券的比例为w，那么投资第二种证券的比例为（1-w）。给定这些参数，两个证券投资组合的总方差可以写成：

要解决这个问题，我们需要找到一个使这个方差最小化的w。

在上述示例中，问题被建模为一个未知变量的函数。我们寻求一个值，使得函数的值最小。首先，我们要明确最小值的含义。

最小值的定义：设𝑆是一个集合，f:𝑆→ℝ是从这个集合到实数的函数。如果在𝑆中的𝑥₀点，f有一个局部最小值，那么𝑥₀的某个邻域满足𝑓(𝑥)≥𝑓(𝑥₀)，对所有𝑥∈𝑈成立。如果对于所有𝑥∈𝑆，都有𝑓(𝑥)≥𝑓(𝑥₀)，那么𝑥₀是全局最小值。

我还没有定义什么是邻域。直观地说，邻域是一个包含接近𝑥点的𝑆的子集。为了判断点是近还是远，我们需要在集合𝑆上定义一些距离度量。幸运的是，实数轴以及任何欧几里得空间都自带了一种自然的距离度量。

如果x和y是n维向量空间中的点，我们可以将它们的坐标写为，

x和y之间的距离由它们的差的范数给出：

微积分定理中的关键结果是解决优化问题的：

定理：必要优化条件

设f：ℝₙ→ℝ是一个连续可微函数。如果𝑓在𝑥₀处有一个局部最小值，那么∇𝑓(𝑥₀)=0。

逆命题并非总是成立，但如果𝑓有二阶导数，那么有一个更强的条件来保证最小值。

当且仅当∇𝑓(𝑥₀)=0且∇²𝑓(𝑥₀)≥0时，𝑓在𝑥₀处有一个局部最小值。

注意，∇𝑓表示向量

在一维情况下，这就是我们熟知的导数𝑑𝑓/𝑑𝑥。下图展示了一个函数的导数为0的点。

这个性质表明了一种寻找最小值的简单算法：找到函数导数为0的所有点。如果有多个，计算函数在每个点的值，并选择最小值。

利用这个算法，我们现在可以解决方差最小化问题：

取方差V关于w的导数，得到

我们将这个表达式设为0，求解w，得到最小方差投资组合的解：

我们有一个在多维度上计算最优性的强大工具。然而，到目前为止，还有一些问题无法解决。考虑以下问题：

我在两点𝑡1和𝑡2之间画出一个函数𝑥(𝑡)：ℝ→ℝ的图像。然后我将图像绕𝑡轴旋转，形成一个表面。这样描述的旋转表面的面积由下式给出：

下面是一个旋转表面的示例

我们感兴趣的是在两个固定点之间找到一个函数，使得旋转表面的面积最小。到目前为止，我们讨论的方法无法解决这个问题，因为我们寻找的不仅仅是一个数，而是整个函数。

上述问题需要优化一个函数的函数。这样的函数通常被称为泛函（Functional）。我们可以将泛函视为一个函数F：V→ℝ，其中V是函数空间。与我们之前处理的域𝑓：ℝⁿ→ℝ具有有限维数的情况不同，这个新的函数空间具有潜在的无限维数。

我们可以在无限维空间中求导数吗？

首先要做的是仔细研究导数的定义，并了解如何将其扩展。在微积分课程中，点𝑥处的导数通常定义为

即使在这个简单的一维定义中，我们也必须小心，因为如果从左侧（h负）或右侧（h正）接近0，可能会得到不同的结果。

定义：变分导数

设𝐹：𝑉→ℝ是一个定义在向量空间V（可能是无限维）上的实值函数。𝐹在𝑥处沿ℎ方向的变分导数定义为

其中𝜖是一个正实数。

注意，这个导数通常取决于方向向量ℎ。如果在计算导数时发现它与ℎ无关，那么这是一个好兆头，因为它意味着导数可能在每个方向上都有良好的定义。

给定一个未知函数x及其导数的已知泛函L，找到使以下积分最小化的函数x：

这是一个无限维空间中的优化问题。事实证明，情况与有限维情况类似，需要寻找I的导数等于0的地方。

𝑥是变量𝑡和𝑥及其导数的函数。 𝐿(𝑥,𝑥˙)可以被视为两个变量𝐿(𝑥,𝑦)的函数。这样的函数𝐿在点(𝑥+𝑒𝑥′,𝑦+𝑒𝑦′)的泰勒展开式为

其中e是一个很小的数。我可以将上式写为

计算导数

现在，使用变分导数的定义

首先，我计算𝐼(𝑥+𝑒ℎ)−𝐼(𝑥)，其中𝑒是一个很小的数，ℎ是一个任意函数。然而，它并不是完全任意的。h必须使端点𝑡₁和𝑡₂处的值保持不变。换句话说，必须有f(x₀)+h(t₁)=f(x₀)，从而得到h(t₁)=0。同样的道理也适用于t₂。下面的图片说明了这一点。

因此，我们得到：

现在我可以使用泰勒展开来得到

注意，O(e²)项可以忽略不计。现在我关心的是括号中的第二项。使用微积分中的莱布尼兹规则：

得到了第二项的表达式：

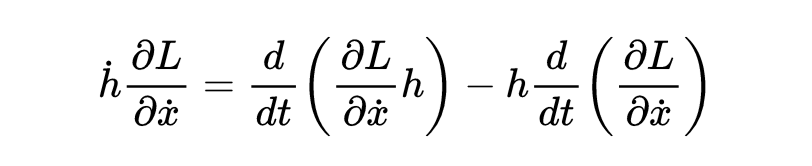
两边积分：

正如我们讨论过的，h必须使端点保持固定，这意味着h(t₁)=h(t₂)=0。因此，上述积分的值为0。

这是剩下的部分

取极限消除了O(e)项。为了找到最优值，我令导数为0。

但由于ℎ是一个（几乎）任意的函数，唯一使这成立的方式是对于每个ℎ，积分项恒等于0。

欧拉-拉格朗日方程

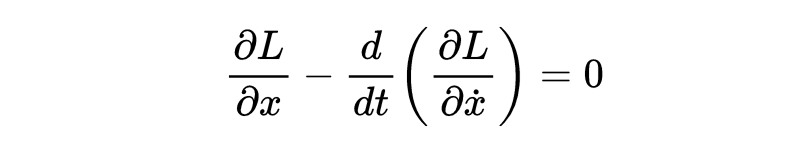
应用：旋转曲面

让我们回到之前遇到的问题。我们想要找到两点之间的旋转曲面，使得其面积最小：

我们现在可以通过使用欧拉-拉格朗日方程来解决这个问题。通过观察，可以看到在这种情况下

由于x(t)没有出现在表达式中，所以关于x的导数为0。然而：

所以欧拉-拉格朗日方程给出：

重新整理得到

这种类型的曲线被称为悬链线，由此产生的旋转曲面被称为悬链面。