
仔细看上图封面的数字排布,大家有没有发现什么规律?
如果你发现规律的话,恭喜你。但我猜测你想到的可能不会超过2种规律,如果真的超过了,说明你很厉害👍!
好,接下来我带大家一起彻底分析下这个数字三角形吧。
01 “杨辉三角”的由来
上篇我们提到过,在宋朝时期我们的古代科技就达到了巅峰时代,这很大程度其实来自数学的探索。
因为在古代,数学总是和天文学以及计时仪器相关联的,也许是有一定的数学基础,而且和外界文明的交往密切,宋代在天文学上也取得了不少成就
比如,北宋的数学家贾宪,他是世界上最早提出二项式分解计算公式的数学家之一。
这项成就在很长的时间里被归功于南宋数学家杨辉的发明,因此这项成就在过去被称为“杨辉三角形”,后来在大英博物馆所藏的《永乐大典》中发现贾宪的《释锁算术》中已经有了这项发现。
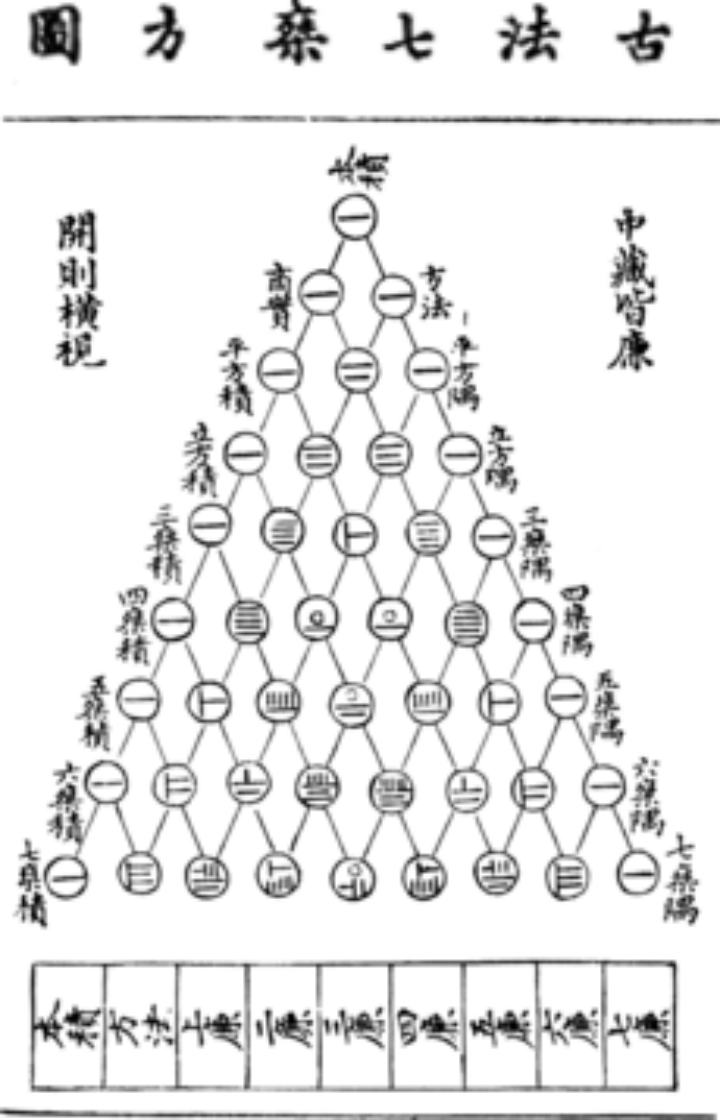
贾宪三角形
基本情况就了解到这了,接下来看看数学知识,大家了解即可。
02 概率论方面
我觉得关于二项式,以前看到这个词都会避而不见,总觉得难得一批。但现在不会这么想了,如果仔细研究的话,这玩意真的很有趣!
甚至有时候我会发现,它能和宇宙的奥秘打通关系呢。
其实,关于“杨辉三角”的概念已经在全世界被研究了一千多年。
在伊朗,它也被称为卡亚姆三角,在许多“西方世界”中,这个数学结构被称为帕斯卡三角形,这归功于法国数学家布莱斯•帕斯卡(Blaise Pascal)对其进行的深入研究。
帕斯卡利用这个三角形来解决概率论中的许多问题,记住这个非常重要!
比如,在概率论中,我们经常需要计算组合数。
例如,假设你有10张牌,从中抽取3张,不考虑顺序,那么有多少种不同的抽取方式呢?
这个问题可以通过帕斯卡三角形来解决,具体来说,就是查找第10行第3列的数字。
而且,帕斯卡三角形与二项分布有着直接的联系。
二项分布描述了n次独立实验中成功k次的概率。
例如,在抛掷硬币的实验中,如果硬币出现正面的概率是p,那么经过n次抛掷后恰好出现k次正面的概率可以用二项式定理表示:

其中,n和k是帕斯卡三角形中的二项式系数。
03 二项式系数
帕斯卡三角形中的数字被称为二项式系数,它们代表了从 n 个物体中选择 k 个的方法数。
举个例子,有6种方法可以从4个对象中选择2个,这对应于帕斯卡三角形的第4行和第2列的位置(从0开始计数)。
你可能还记得基本代数中的一些公式,例如:

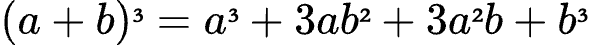
帕斯卡三角形的第二行和第三行中的系数正是这些公式中的系数,这绝非偶然。
这种现象在数学上被称为二项式定理,它在一般情况下都成立。所以老师以前让我们默写二项式公式,如果记住这个三角形就可以啦。
帕斯卡三角形中最基础的图案之一是沿着三角形边缘排列的1。
与这些边缘平行的,是自然数序列1, 2, 3, 4, 5, ...。

再往三角形内的一条平行线中,你会找到三角数:1, 3, 6, 10, 15, 21, ...。
这些数字可以排列成一个三角形,并且可以通过对自然数进行累加得到。
例如,数字10是通过1 + 2 + 3 + 4得到的,它表示一个三角形状的球的数目。
在帕斯卡三角形中,第三条平行线是四面体数列,从1, 4, 10, 20, ...开始。
这些数字表示的是四面体形状(即三角形底部的金字塔)的球数。
这些模式在三角形中以其独特的方式继续存在,展示了数学之美的多样性。
04 幂
帕斯卡三角形的一个有趣特性是,每个“方向”都能生成一个新的图案。例如,如果你将每一行的数字相加,你会得到2的幂数:

1, 2, 4, 8, 16, ...
相应的公式可以通过二项式定理证明,展示了数学中的一致性和逻辑之美。

05 曲棍球棍定理
帕斯卡三角形还有一个令人惊讶的性质:如果你沿对角线将数字相加,然后再向边上移动一步,你会得到对角线数字的总和。
下面的图示对此进行了解释:

曲棍球棍定理图示
这个小练习展示了帕斯卡三角形中的另一种模式,进一步揭示了数学中的巧妙关联。
06 数学分形
如果我们对帕斯卡三角形进行模2运算(将偶数变为0,奇数变为1),我们会得到一个令人惊叹的图案。
通过这种方式,我们可以将帕斯卡三角形转化为谢尔宾斯基三角形(Sierpinski triangle),这是一个著名的分形。

三角形展示了分形的无限复杂性,即使从最简单的数学结构中也能发现如此复杂和美丽的图案。
看一下动图:
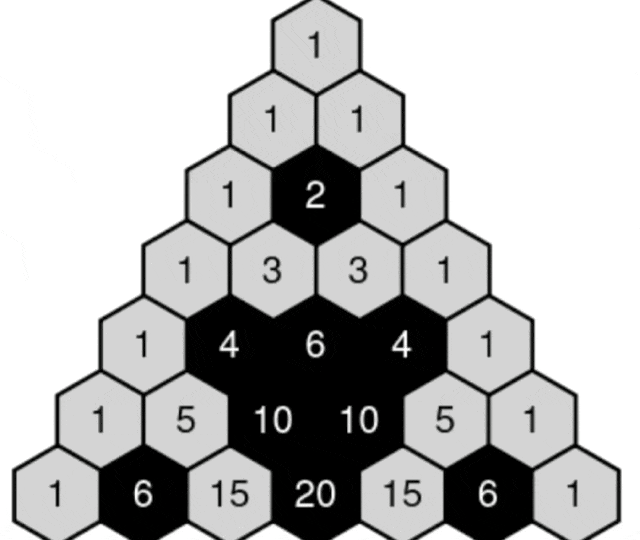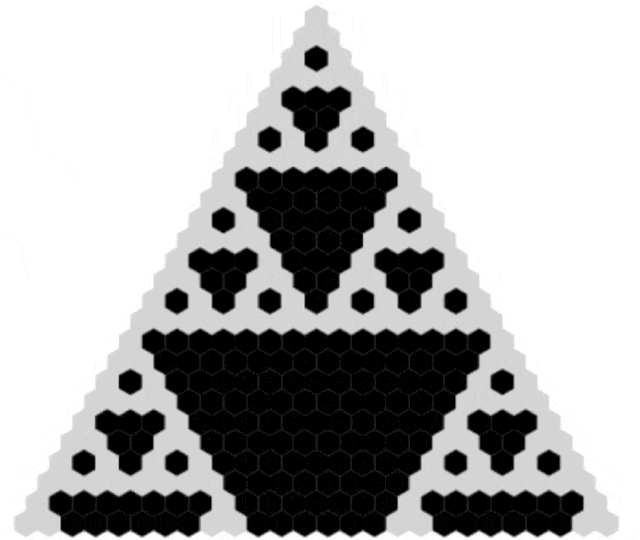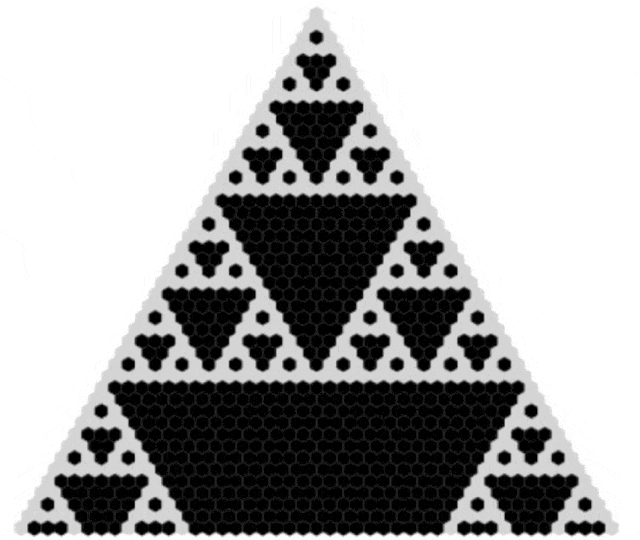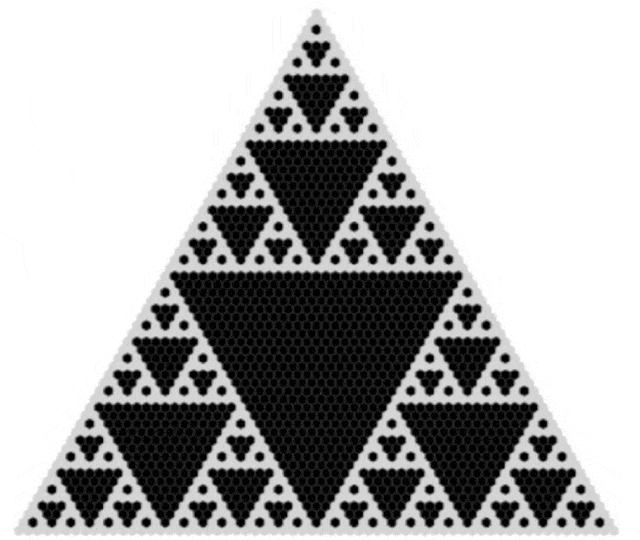
GIF from Wikimedia Commons
07 二进制数的奥秘
如果我们把帕斯卡三角形中的数字减去mod 2,那么我们就得到了一个特殊版本的三角形:

图源 aperiodical.com
如果我们将每一行看作一个二进制数,我们会得到一个有趣的序列:1, 3, 5, 15, 17, 51, 85, 255, 257... 这个序列乍一看似乎没有明显的规律,但如果将每个数字分解为质因数,我们会发现:
1
3
5
15 = 3 * 5
17
51 = 17 * 3
85 = 17 * 5
255 = 17 * 3 * 5
257
这个规律是通过将前面的数字组合相乘来生成下一个数字。
这里的质数不仅是费马质数(形如2^(2^n) + 1的质数),而且这条序列中是否包含无限多个质数至今仍是一个未解之谜。
08 斐波那契数列的隐藏
斐波那契数列在自然数中无疑是明星。
这个序列从1, 1, 2, 3, 5, 8, 13, 21,... 开始,后续的每一个数字都是前两个数字之和。这一序列与黄金分割比φ有着密切的联系。
更有趣的是,斐波那契数列也隐藏在帕斯卡三角形中。如果你对如下图所示的对角线求和,你会得到斐波那契数列:

这无疑是数学中的另一个奇迹。用二项式系数来证明这一点是一个非常有趣的数学练习,甚至可以通过数学归纳法来完成。
总结:
总之,关于帕斯卡三角形中的模式还有很多等待我们去探索。
事实上,直到今天,数学家们还在发现新的模式。这种数学之美是无穷无尽的,不断给予我们新的惊喜。
谁知道我们在第一百万行帕斯卡三角形中会发现什么?
我只能说,之前小看它了!
