在数学建模中,我将“数”、“式”、“形”可以视为三大基础模型。它们构成了数学建模的核心框架,并相互作用,共同实现对问题的全面描述和解析。下面我来具体谈谈三者的内涵及关系。
一、数:建模的基础“数”是数学建模的起点,它体现了现实世界的数量关系。解决问题过程中的数据的收集、处理和分析是建模的重要基础。通过“数”,我们能够捕捉问题的基本量化特征。
数在建模中的角色包括:描述现象。数据用于量化描述现象,例如一组温度数据反映了气候变化的趋势。
揭示关系。数据可以通过统计分析或机器学习方法挖掘变量之间的相关性,例如商品价格和销售量之间的关系。
验证模型。数据用于评估模型的有效性,例如通过残差分析判断模型的拟合程度。
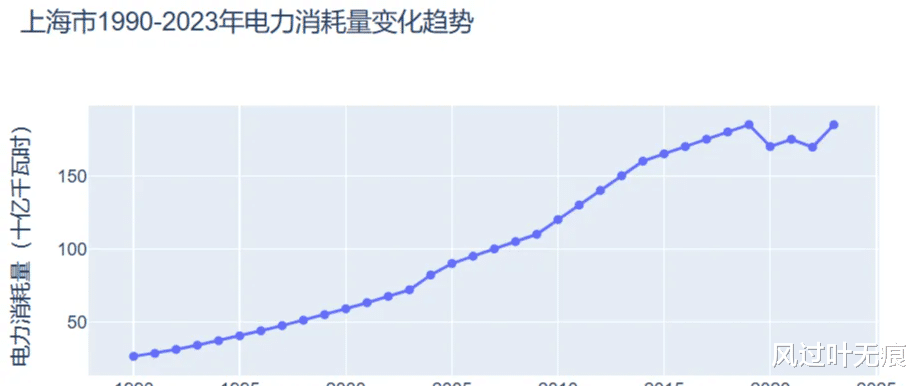
假设我们研究上海每年的电力消耗量,采集的数据可以表示为时间序列:
其中 表示第 年的电力消耗量。
年份电力消耗量(十亿千瓦时)199026.474199128.500199231.200199334.100199437.200199540.500......2015165.0002016170.0002017175.0002018180.0002019185.0002020170.0002021174.9622022169.6012023184.900数据来源:国家统计局、中国电力企业联合会
通过统计分析,我们可以得到一些基本的描述性统计量,比如平均值,
方差:
这些数据特征为进一步建模提供了基础。
二、式:关系的抽象“式”是对“数”的进一步抽象,用数学语言表达变量之间的内在关系。它可以是函数、方程组、不等式或优化模型,依赖于问题的复杂程度和研究目标。
式在建模中的角色包括:构建模型。将数据关系转化为数学形式,例如线性回归模型:
其中 是误差项。
描述变化。微分方程是描述动态变化过程的常用工具,例如人口增长模型:
其中 是人口规模 是增长率 是环境容量。
优化决策。优化模型用于寻找最佳方案,例如线性规划问题:
假设我们要预测未来某工业企业的生产成本,可以建立以下函数关系:
其中 是固定成本 和 是模型参数。
三、形:直观的表现“形”是“数”和“式”的可视化,是模型的重要表达形式之一。在几何意义上,“形”用于揭示数据和函数关系的直观特性;在实际应用中,它帮助我们理解模型结果并作出解释。
形在建模中的角色包括:
直观展示。数据和模型的图形化表达可以清晰地展示规律,例如散点图展示变量之间的相关性、折线图可以展示随时间变化的动态关系。
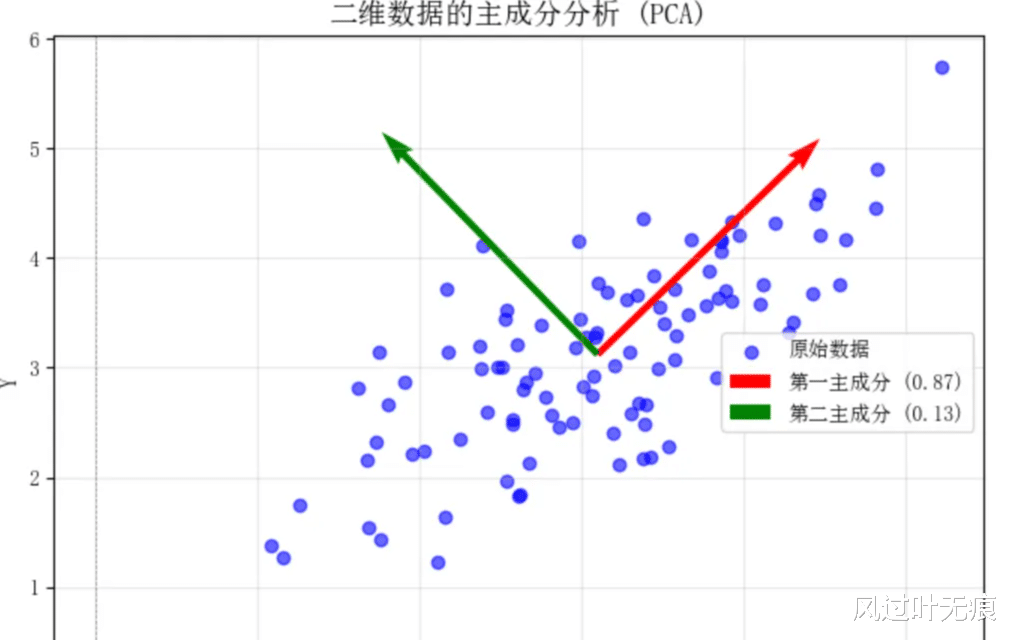
揭示结构。几何模型能揭示复杂关系中的结构特征,例如通过主成分分析(PCA)找到高维数据的低维特征。
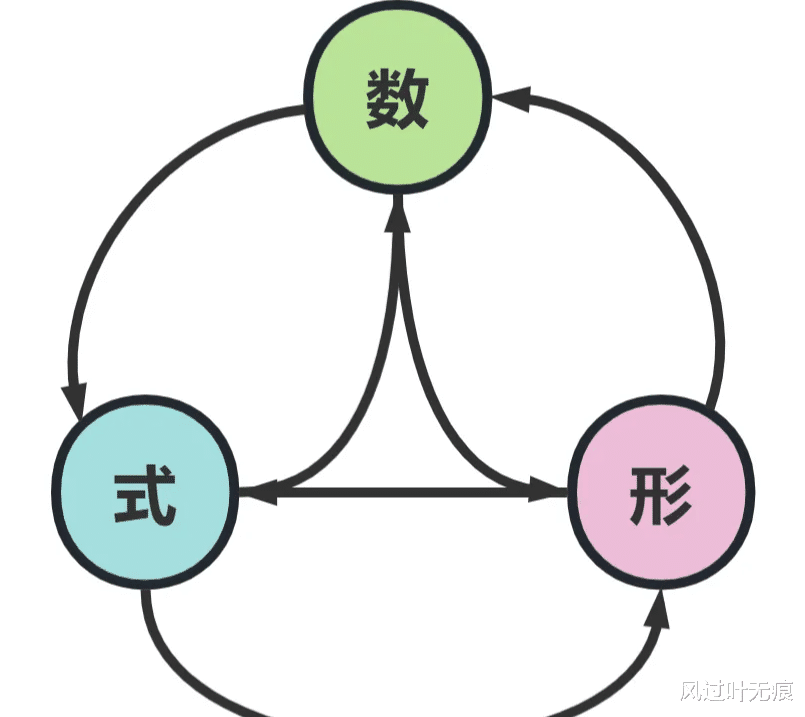
我们还可以通过因果图来揭示因果关系,比如

辅助验证。图形化结果用于评估模型的适用性,例如绘制拟合曲线或残差图。
假设我们研究函数 的行为,其一阶导数为:
通过绘制函数曲线 和,可以直观观察其增长和减速趋势,辅助我们分析函数的极值点和单调性。
四、三者关系:交融与互补尽管“数”、“式”、“形”各自独立,但它们在建模中密不可分。三者的关系可以概括为:
数生式: 数据提供构建数学模型的依据。通过对数据的统计分析,我们能够发现变量间的关系,进而建立模型。
式释形: 数学表达转化为图形后,模型结果更直观、更易解释。通过图形分析,我们可以验证模型的假设并优化参数。
形返数: 图形化的结果反过来帮助我们调整数据的采集和处理方式。例如,残差图中的系统偏差可能提示数据中存在未捕捉的规律。
数释形: 数据通过图形化呈现,可以直观地揭示数据分布的模式和特征。例如,通过散点图或直方图,我们可以初步了解数据的趋势或分布情况,为建模提供启发。
式生数: 数学表达可用于生成数据。例如,通过数学模型模拟环境中的温度变化或预测未来的经济增长,产生虚拟或预测数据,作为进一步研究的基础。
形释式: 图形化展示可以帮助我们从视觉上发现潜在的数学关系,从而指导数学表达的构建。例如,散点图中的线性趋势可能提示我们使用线性回归模型,而周期性波动可能指向正弦函数的使用。
这六种关系相辅相成,共同构成了数学建模中的核心逻辑链条。在实际建模过程中,我们需要灵活运用这些关系,确保模型的构建过程既有数据支持,又具备数学严谨性,同时能够通过可视化手段验证和优化。
“数”、“式”、“形”作为数学建模的三大基础模型,为问题的分析和解决提供了基础的框架,是更为复杂与集成模型的基础。在学习和实践中,我们应注重三者的结合,通过数据驱动、数学表达与几何直观实现建模能力的全面提升。通过数学建模实现:复杂问题简单化,简单问题深刻化,深刻问题具体化。
