许洪喜
《物质结构与性质》中晶胞的计算是难点。晶胞的计算主要考查学生对晶胞中微粒空间位置分析和综合运算等关键能力,有助于学生空间观察、空间想象能力与定量分析能力的提升,有利于培养学生严谨的定量运算思维品质、宏观辨识与微观探析的核心素养。本文以近五年山东高考化学试题为例,回顾有关晶胞计算的情境素材和考点,探寻命题的规律和方向,并进行思维建模。希望能够对解决此类问题有所帮助。
一 近五年山东高考考情分析
(一)情境素材再现
近五年山东高考中有关晶胞计算的情境素材见表1。

(二)有关晶胞计算涉及的考点
近五年山东高考有关晶胞计算涉及的考点统计见表2。
(三)备考启示
1.历年的试题都给出了晶胞图示且比较复杂,有的是我们熟悉的,如2024年MnOx的晶胞结构(金红石型结构);有的是陌生的,但是再仔细观察并分析一下就会发现它们是一些简单晶胞、典型晶胞的“变型”“叠加”,如2021年XeF2的晶胞图示,大球(Xe原子)类似于体心立方堆积(是长方体而非立方体);2020年CdSnAs2的晶胞结构图示,Cd、Sn和As原子围成了两个金刚石型结构,上下“叠加”。所以,当我们遇到相对陌生的、复杂的晶胞时,一定要静下心来,将其转化为一些熟悉的、典型的晶胞的“变型”或“叠加”后再进行分析推断。
2.分析历年试题涉及的考点可以看出微粒数目的有关计算是近几年高考的高频考点,利用晶胞参数计算晶胞密度、距离、分数坐标等也是高考的重点,晶胞参数常用的单位有cm、nm、pm等,在计算时一定要关注单位间的换算,明确不同单位间的换算关系。
3.2024年试题中出现了xy平面的投影图,有些学生看不懂,2019年全国Ⅰ卷出现过“沿立方格子对角面取得的截图”,也是当年高考题中的难点,所以这些新型的图示也是备考时需要思考的问题。
4.历年试题均考查了四方晶系即平行六面体晶胞,还没有考查过六方晶胞,所以我们要格外重视六方晶胞的相关计算。另外有关晶胞中空间利用率、八面体空隙、四面体空隙等还没有考查到的考点及全国各地高考创新的设问形式,也是复习备考时需要重点关注的地方。
二 有关晶胞计算的思维建模
(一)有关晶胞中微粒数目的计算
【例1】(2024年山东卷16题节选)某种氧化物MnOx的四方晶胞及其在xy平面的投影如图所示,该氧化物化学式为____。

【答案】MnO2
【解析】本题结合投影图来判断微粒的位置,进而利用均摊法计算出微粒的数目,得到化学式,体现了宏观辨识与微观探析的核心素养。若对金红石型(TiO2)晶胞比较熟悉,不用借助投影图就能快速得到答案;若不熟悉,根据题图以及该晶胞为四方晶胞,由均摊法可以得出,一个晶胞中Mn的数目为 1+8× 1 8 =2,Ο 的数目为 2+4× 1 2 =4 ,所以该氧化物的化学式为MnO2。
【思维建模】1.利用均摊法进行晶胞中的微粒数目计算:假设某个微粒为N个晶胞所共有,那么一个晶胞占有该微粒的 1 Ν 。在使用均摊法计算晶胞中微粒数目时,要注意晶体的晶胞的形状(晶系)。不同形状的晶胞,相同位置的微粒共有情况可能是不同的。如立方晶胞中微粒数目的计算方法如图1所示,而在六棱柱晶胞中,位于顶角上的微粒为6个晶胞共有,侧棱上的微粒为3个晶胞共有,底面的棱上微粒为4个晶胞共有,面上的微粒为2个晶胞共有。

2.典型晶胞不同方向的投影图见表3。
(二)有关晶胞中微粒的分数坐标的计算
【例2】(2020年山东卷17题节选)四方晶系CdSnAs2的晶胞结构如图所示,晶胞棱边夹角均为90°,晶胞中部分原子的分数坐标见下表。

一个晶胞中有____个Sn, 找出距离Cd(0,0,0)最近的Sn(用分数坐标表示)。CdSnAs2 晶体中与单个Sn键合的As有____个。
【答案】4 (0.5,0,0.25)、(0.5,0.5,0) 4
【解析】本题的难点在于原子的分数坐标和晶胞中位置间的快速转换,若把该晶胞看作是两个金刚石型的晶胞上下“叠加”,这样可以快速判断出各原子的相对位置。第一个空由表中Cd原子的分数坐标为(0,0,0),可知有Cd原子位于顶角,故图中黑球代表Cd原子;同理由表中Sn原子的分数坐标为(0,0,0.5),可知有Sn原子在棱上,故图中白球代表Sn原子,剩下的灰球代表As原子,观察图中的Sn原子,会发现4个在棱上,6个在面上,所以一个晶胞中有4个Sn; 第二个空,离原点最近的Sn有两个,距离均为 2 2 a pm,一个在底面面心,即(0.5,0.5,0),另一个在侧面面上,即(0.5,0,0.25);第三个空由图可看出面上的Sn(实际占有 1 2 ) 结合了两个As,所以CdSnAs2晶体中与单个Sn结合的As有4个。
【思维建模】1.原子分数坐标的确定方法:先依据已知原子的分数坐标确定坐标系取向。再以坐标轴所在棱长作为1个单位,从原子所在位置分别向三个坐标轴作垂线,得到的三个坐标轴上的截距就是该原子的分数坐标。坐标数值可以是分数,也可以是小数。
2.原子分数坐标与晶胞中位置间的关系:三个坐标的数值中,若均为分数,则在体内;若两个为分数,则在面上;若一个为分数,则在棱上;若没有分数,则在顶角。
3.典型晶胞中原子的分数坐标见表4。
(三)有关晶体密度的计算
【例3】(2023年山东卷16题节选)一定条件下,CuCl2、K和F2反应生成KCl和化合物X。已知X属于四方晶系,晶胞结构如图所示(晶胞参数a=b≠c, α=β=γ=90°),其中Cu化合价为+2。若阿伏加德罗常数的值为NA,化合物X的密度ρ=g·cm-3(用含NA的代数式表示)。

【答案 】 4.36×10 32 abcΝ A
【解析】本题的创新点在于没有直接指出哪种球代表哪种原子,所以需要先根据X属于四方晶系,观察图由均摊法计算出,该晶胞中含有黑球的个数为 8× 1 4 +2=4 、白球的个数为 16× 1 4 +4× 1 2 +2=8 、灰球的个数为 8× 1 8 +1=2 ,再根据化合价代数和为0,推断出X为K2CuF4。由晶胞的质量为 2×218 Ν A g ,晶胞的体积为abc pm3=abc×10-30cm3,可得出化合物X的密度 ρ= 2×218 Ν A g abc×10 -30 cm 3 = 4.36×10 32 abcΝ A g⋅cm -3 。
【思维建模】1.密度计算方法如图2所示。
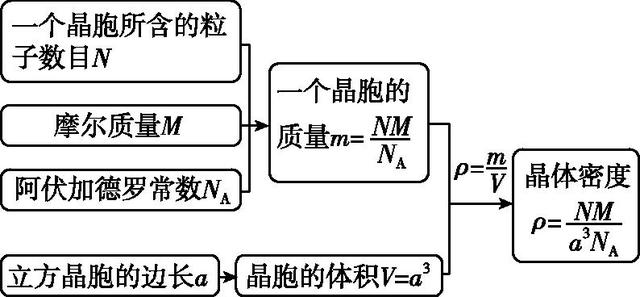
2.注意常用单位间的换算:
1 nm(纳米)=1×10-9 m=1×10-7 cm
1 pm(皮米)=1×10-12 m=1×10-10 cm
3.典型晶胞密度的计算方法见表5(设晶胞参数均为a cm)。

(四)有关晶胞中微粒间距离的计算
【例4】(2021年山东卷16题节选)XeF2晶体属四方晶系,晶胞参数如图所示,晶胞棱边夹角均为90°,该晶胞中有____个XeF2分子。以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称为原子的分数坐标,如A点原子的分数坐标为 ( 1 2 , 1 2 , 1 2 ) 。已知Xe—F键长为r pm, 则B点原子的分数坐标为____;晶胞中A、B间距离d=____pm。

【答案 】2 ( 0,0, r c ) 1 2 a 2 +( c 2 -r ) 2
【解析】本题将共价键的键长融入晶胞的计算中,非常新颖,解题的关键在于弄清图中Xe—F键长和晶胞参数间的关系。大球类似于体心立方堆积,小球8个在棱上,2个在体内,由均摊法可知该晶胞中有2个XeF2分子;由分数坐标 ( 1 2 , 1 2 , 1 2 ) 可以知道A点原子在晶胞的体心,根据题干中原子的分数坐标的定义可知z轴的单位长度为c pm, B点与原点的距离为r pm, 故其坐标为 ( 0,0, r c ) ;做辅助线y垂直于x,如图所示。

其中 x= c 2 -r,y= 2 2 a ,所以 d= x 2 +y 2 = 1 2 a 2 +( c 2 -r ) 2 pm,也可以先写出A、B的实际坐标: A( 1 2 a, 1 2 a, 1 2 c ) 、B(0,0,r),由两点间距离公式求得。
【思维建模】1.晶胞中微粒间距离的计算方法:第一种方法是通过做辅助线,利用三角形中的三边关系进行计算;第二种是先写出两个微粒的实际坐标,再根据两点间距离公式进行计算。
2.典型晶胞中“距离最近”的微粒间的距离见表6(设以下晶胞参数均为a)。

总而言之,有关晶胞的计算,计算微粒数目是根本,确定微粒位置是关键,计算晶体密度是重点。所以只要在备考时打牢基础知识、学会思维建模、树立解题信心,就一定会成功逾越晶胞的计算这座高山。
