有人告诉我，我在书中加入的每一个方程式都会使销售量减半——霍金

牛顿引力与狭义相对论是不相容的，因为在牛顿的理论中，引力在任何距离上都是瞬时作用的。狭义相对论不允许这一点，而是强加了一个自然的速度极限——光速。为了调和相对论和引力，我们现在需要从狭义相对论的（平坦的）)=闵可夫斯基空间移动到广义相对论的弯曲时空。爱因斯坦在形成广义相对论时的伟大见解是：

物质和能量会扭曲时空

时空可以用一种被称为伪黎曼流形的数学结构来建模。

因此，广义相对论中的引力不再被视为一种力，而是时空几何的一种属性。

为了理解弯曲空间的几何概念，米斯纳等人以一只蚂蚁在苹果皮上爬行为例。蚂蚁决定尽可能走得笔直，于是仔细地量了量自己的步子，使其长度相等。如果蚂蚁冒险太靠近苹果的顶部，即使它试图走直线，也会发现自己被拉进苹果顶部的凹窝里。一个有想象力的人可能会说，有一个力把它吸引到苹果的凹窝里。当然不存在力。蚂蚁的路径不是由外力决定的，而是由苹果表面的曲率——几何形状——决定的。米斯纳想象一个物理系的学生看着蚂蚁的行进，然后拿起一把刀，小心地把蚂蚁走过的苹果皮的痕迹切下，放在他的书上。在观察到轨道“像激光束一样直”之后……这只蚂蚁没有比这更“经济”的路径来“覆盖”这10厘米的果皮了”，这只蚂蚁的路径形成了“一条美丽的测地线”。

狭义相对论中的（平坦的）闵可夫斯基空间存在于深空，远离任何引力场的影响。在平坦的时空中，自由粒子沿直线运动。在大质量物体附近的时空是弯曲的。包括光在内的自由粒子将不会沿直线运动，而是沿着弯曲时空的几何形状所决定的“可能最直”的路径运动，就像蚂蚁沿着苹果表面所决定的可能最直的路径运动一样。

这些路径被称为测地线，我们可以粗略地定义为弯曲空间中两点之间的最直或最短距离。例如，球面上的测地线是大圆的一部分（与球面直径相同，圆心为球面中心点，如赤道，或任何经度线的圆）。如果时空的数学结构是已知的——即它是如何弯曲的——那么运动的粒子（以及行星和恒星）的测地线就可以通过观测来计算和测试。

为了在数学上描述弯曲空间，我们使用流形的概念，广义地定义为局部平坦的光滑弯曲空间。例如，一个圆是一个一维流形：使它足够大，小段看起来像一条直线。球体的表面是二维流形：它的小块看起来是平的。时空，一种四维流形，在局部也是平坦的，并且在足够小的区域内，就会简化为狭义相对论中的时空。

我们说流形是n维的，因为流形上的每个点都可以用n维或坐标来表示。线和圆是一维流形：它们上的任何点都可以用一个坐标来描述（例如，线沿直线的距离，圆的极角）。平面是一个二维流形，就像球体的表面一样：表面上的任何点都可以使用球面极坐标θ和φ来描述。正如我们所看到的，时空是四维的，需要一个时间坐标加上三个空间坐标来确定时空中的一个点。

并不是所有的空间结构都是流形。从平面上显现出来的一维直线不是流形，两个锥尖之间彼此重叠也不是。因为这些物体不是局部的欧几里得，所以它们不属于流形。

黎曼流形和度规

为了能够模拟广义相对论的时空，流形还必须具有这两个附加属性：

它一定是可微的。当我们看张量的变换性质时，这将变得非常清楚，因为它包含了大量的偏导数。

它必须被赋予一个对称度规张量，在狭义相对论中，它定义了流形上附近点的间隔。度规的形式将通过流形改变，这取决于该区域的时空如何弯曲。例如，在远离物质和能量影响的深空，时空将近似于狭义相对论中的闵可夫斯基空间。在一个不旋转的黑洞附近，将近似史瓦西度规。度规完全定义了流形的曲率，因此在相对论中具有根本的重要性。

一个可微的和具有对称度规张量的流形被称为黎曼流形。黎曼发现度规包含了我们描述流形曲率所需要的所有信息。如果我们知道度规，我们就知道空间。这就是为什么度规对广义相对论至关重要。

n维黎曼流形的线元为：

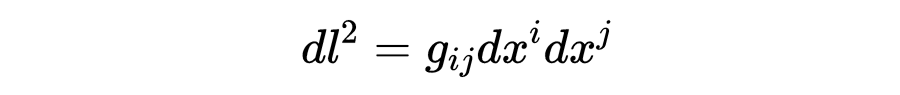
其中

是度规，

是坐标微分，它意味着度规决定了线元的系数。当我们遇到笛卡尔坐标中的三维欧几里德线元素时，我们看到了一个简单的例子

欧几里得度规是：

在上面的欧几里德线元中有1 × dx^2, 1 × dy^2和1 × dz^2。我们也看到过笛卡尔坐标下的闵可夫斯基线素

闵可夫斯基度规是

上述闵可夫斯基线元中有1 × c^2dt^2、-1 × dx^2、-1 × dy^2、-1 × dz^2。

顺便说一下，我们知道这些度规描述了平坦空间，因为它们的度规系数是±1。然而，如果我们选择一个奇怪的坐标系，我们很可能最终得到一个复杂的度规，其系数不等于±1。

我们如何判断度规是否定义了平坦空间?答案是黎曼曲率张量，这是确定流形是平的还是弯曲的绝对苛刻的测试。如果黎曼曲率张量对于特定空间中的所有点都是零那么这个空间就是平坦的。如果张量在某一点不等于零，那么空间在那一点是弯曲的。

当我们想到圆或球面时，我们认为它们存在于日常的欧几里德空间中。我们可以在一张坐标纸上画一个圆，或者把一个球放在桌子上。然后我们可以把圆的曲率和画在坐标纸上的直线相比较，或者把球体的圆度和桌子的平坦度相比较。

在数学术语中，我们说圆和球表现出外部曲率，因为它们的曲率与一个更高维度的外部空间有关——纸张是二维，桌子是三维。然而，并不是所有的流形都可以被认为以这种方式嵌入到外部空间中。我们常常需要根据流形本身的条件来研究它，也就是说，不需要参考更高维度的空间。这种类型的曲率称为本征曲率。

我们通过直接检查它们来理解本质上弯曲的流形，使用从度规衍生出来的度量和数学工具来分析它们的内部结构。在广义相对论中，我们只对时空的固有曲率感兴趣。

把一个卷起来的圆柱体放在桌子上，我们可以看到它与桌子的平面相比具有外部曲率。然而，本质上，圆柱体是平的——画在其表面上的三角形内角之和等于180°。这并不奇怪，因为我们可以展开圆柱体，最后得到一张平坦的纸。

和圆柱体一样，桌面上的球有一个外曲面。然而，球的表面本质上也是弯曲的。在球面上，经度线在赤道上平行，但在两极相交。另外，球面上三角形的内角可以都等于90度。与圆柱体不同的是，球面不能在不变形的情况下被平坦化，地图绘制者在试图将地球表面投影到平面地图上时发现了这一点。

球的表明

球面是最简单的二维流形之一。

之前，我们遇到了用球坐标描述欧几里德三维空间的线元和度规。线元为

如果我们将极坐标R设为某个常数r，我们就失去了dr项，并且定义了球面的线元：

它使用两个极坐标(θ， ϕ)描述一个二维表面。我们知道，使用坐标(θ， φ)的这个表面的度规是

其中

逆度规是

对于单位半径球(R = 1)，这些度规变成

时空流形是相对论的舞台。下面我们将看到在舞台上表演的主要演员。这些数学对象被称为标量、逆变向量、1-形式（对偶向量、协变向量）和张量。