为了满足你的好奇心，把你从数学术语中解救出来，简单的解释是：

x = 1 + 2 + 4 + 8 + …

x = 1+ (2 + 4 + 8 + …)

x = 1+ 2(1 + 2+ 4 + 8…)

x = 1+ 2x

x = -1

这与计算收敛无穷级数的方法几乎完全相同。但对于收敛级数，如1/2 + 1/4 + 1/8 + 1/16…很容易可视化和理解，而发散级数则不然。

发散与收敛

收敛级数是其和趋于某个数字的级数。例如，收敛级数1/2 + 1/4 + 1/8 + 1/16 +…显然趋近于某个极限，即1，如下面的几何图所示。

我们也可以用它们的“部分和”来区分发散和收敛。顾名思义，“部分和”是数列中一部分项的和。我们可以用几何级数的公式表示1/2 + 1/4 + 1/8的前n项的部分和。

通过这个公式，我们看到一个收敛级数的部分和似乎趋近于1，这在函数图中更加明显。

然而，在发散的情况下，部分和不趋近于一个值，而是发散到无穷大。

计算发散级数的“规则”

定义（正则）：如果级数的求和方法给出了收敛级数的正确答案（即部分和数列的极限），则求和方法是正则的，

线性

要成为线性的，和必须是可分配和可分解的：

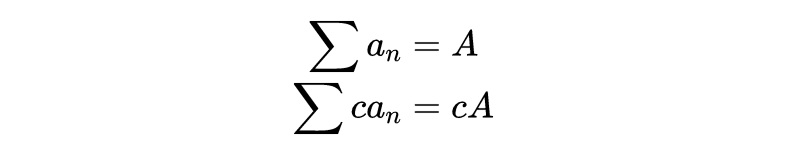
在线性条件下，长度相等的和的项可以分组，

稳定性

定义：当可以从求和中“提取”项时，求和方法就具有稳定性，

并不是所有级数求和方法都满足这些条件（特别是稳定性）。注意，大多数对级数求和的方法并不适用于每个级数；目标是找到并使用尽可能多有趣和重要的级数相加的方法。

线性与稳定性结合

x = 1 + 2 + 4 + 8 + …

(1) x = 1+ (2 + 4 + 8 + …)

(2) x = 1+ 2(1 + 2+ 4 + 8…)

x = 1+ 2x

x = -1

显然，这个发散级数的极限是无穷大，而我得到了一个有限值答案。但我们可以证明它确实符合线性和稳定性，

(1) x = 1+ (2 + 4 + 8 + …)

在(1)中，我们可以从求和中提取一项，这相当于

因此我们可以说求和法是稳定的。

(2) x = 1+ 2(1 + 2+ 4 + 8…)

对于(2)我们可以从和式中提出2，这就等于

这表明级数是线性的。

有了这个，就得到了1 + 2 + 4 + 8 + … = -1的答案。

这个答案似乎都很奇怪，但请注意，它们都代表了一个已知几何级数公式的延续，

在微积分中，我们知道，只有当r∈（-1，1）时，级数才收敛。得到上述例子答案的一种方法是使用这个公式，但要代入收敛区间之外的值，即r= 2。当然，这不是一般的求和方法，但它确实给了我们一种直观的感觉，让我们知道答案是从哪里来的。

蔡查罗求和

蔡查罗求和的方法如下：取无限级数部分和平均值的极限。假设一个级数，

s_k是其第k个部分和，那么

k趋近于无穷大时的极限（如果存在）就是级数的极限。

例如，1-1+1-1+1-1+……，部分和是1,0,1,0,1……，级数是不收敛的，因为这个数列的极限不存在。但是部分和的平均值级数是，

它收敛与1/2，所以这个级数（1-1+1-1+1-1+……）是蔡查罗可求和的吗，答案是1/2。

蔡查罗可求和性允许某些具有振荡部分和序列的级数被“平滑”，但如果级数的部分和变成无穷大（如调和级数），部分和的平均值也会达到无穷。本文的例子“1 + 2 + 4 + 8 + …”不可蔡查罗求和。

阿贝尔求和

阿贝尔求和涉及幂级数的极限：如果极限存在，定义

这说明如果级数收敛，那么上面方程右边的极限存在并且等于这个和。注意1-1+1-1+1-1+……是可阿贝尔求和的，因为

事实上，任何可蔡查罗求和的级数也是可阿贝尔求和的，它们的和是一样的。因此，阿贝尔可求和性更强。

黎曼zeta函数正则化

利用复值函数的解析延拓定义了一些求和方法。函数f的解析延拓是函数g，它定义在比f更大的集合上，它在定义域上处处可微。

最具启发性的例子是黎曼zeta函数

只有当复数s的实部Re(s)大于1时，级数才收敛，但是有一个函数方程，它将zeta函数扩展为一个除了s= 1之外都定义良好且处处可微的函数。这个函数方程可进行如下计算，

所以代入s=-1到zeta函数的级数表示中，得到，

结果证明，这个和在弦理论和量子力学一维卡西米尔效应的计算中有实际应用。

函数

可能会收敛在一个复半平面上，但如果它可以解析地延拓到定义为s= -1的函数，则可以将函数在-1处的值与级数的和联系起来。注意，这种方法是稳定的，但不是线性的。

狄利克雷级数正则化

另一个有时被称为zeta函数正则化的概念是狄利克雷级数

如果f可以解析延拓到0，那么将f(0)的值赋值给右边。这是一种不同于zeta函数正则化的方法，它是线性的，但不稳定。

发散级数的和通常在物理中有应用，如1+2+3+4+……，一般的思想是，如果一个物理情况由一个函数f描述，这个函数f由一个级数定义，它只收敛于一些不包括s的值集，那么f的解析延拓g有一些更大的值集（包括s），它与f密切相关，以至于g(s)可以有一些有意义的物理解释，即使f(s)没有定义。

仅仅是对无穷发散级数的研究就能让我们得到一些有趣的见解，正如莱昂哈德·欧拉向我们展示的那样——对数学整体有深刻的发现。