
求二次函数的极值有着许多实际的应用,下面我们举几个例子。
例3.在墙旁的一块空地上,准备靠墙用36米长的篱笆围一块矩形的空地,种植蔬菜。问怎样围法,才能使所围成的园地的面积最大?这时面积是多少平方米?

分析 如图(图4.15),折线 ABCD 表示篱笆,如果 AB = CD =x(米),那末 BC = AD =36-2x(米).矩形的面积是
y = x (36-2x)(平方米).
所以本题只要求函数 y = x (36-2x)的极大值.
【解】设篱笆的宽是x米,那么它的长就是36-2x米。
又设矩形的面积是 y 平方米,那么有
y = x (36-2x)
=36x-2x²
=-2(x²-18x)
=-2(x-9)²+162.
当 x =9的时候,二次函数 y =-2(x-9)²+162有极大值162.
这就是说,当篱笆的宽是9米时,可以围成最大面积的园地,这块园地的面积是162平方米。
例4. 窗的形状是矩形上面加一个半圆(图4.16),它的周长等于6米。要使窗能够透过最多的光线,它的尺寸应该怎样设计?

分析 这个问题就是要求出半圆的半径是多少米的时候,图形有最大的面积。因此要先求出图形的面积 y (平方米)和半圆的半径 x (米)间的函数关系。
【解】设半圆的半径是x米,那么半圆的长就是πx米,矩形的底BC就是2x米,而矩形的高AB和CD就是½(6-πx-2x)米。设图形的总面积是 y 平方米,那末
y=½(6-πx-2x)·2x+½πx²
就是

由此可知,当 X

的时候, y 有极大值。
所以尺寸应该这样来设计:半圆的半径是

R≈0.84米,或者说矩形的底边长是
BC≈1.68米.
温馨提示:二次函数的一般式y=ax²+bx+c可以通过配方法化为顶点式y=p(x-h)²+k,其中

顶点坐标为(h,k)。(详情请参阅本系列讲座之二次函数的图像那一期)
例5.快艇和轮船分别从 A 地和 C 地同时开出,各沿着箭头所指方向航行(图4.17)。快艇和轮船的速度分别是40公里/小时和16公里/小时。已知 AC =145公里,经过多少时间以后快艇和轮船之间的距离最短?(图中 AC ⊥ CD .)
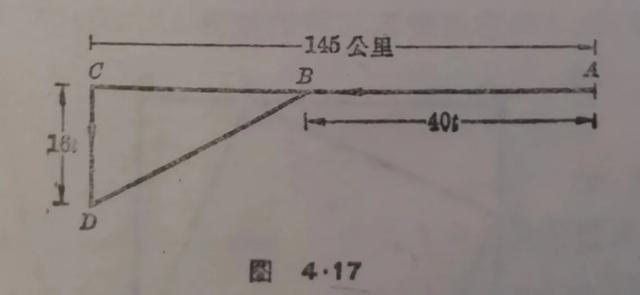
图4.17
【解】设经过 t 小时以后,快艇的位置在 B ,轮船的位置在 D 。这时,
AB =40t公里,
CD =16t公里,
BC =(145-40t)公里.
根据勾股定理得
BD²=BC²+CD²=(145-40t)²+(16t)²
现在要使 BD 最短,就只须使上式右边
(145-40t)²+(16t)²
有最小的值.
令
y=(145-40t)²+(16t)²
=1856t²-11600t+21025,
这个二次函数在
t =11600/3712=3⅛
的时候有极小值。所以,快艇和轮船分别从 A 地和 C 地开出3又⅛小时的时候,它们间的距离最短.
习题4·5(2)1.已知一个正方形 ABCD 。现在从它的四个顶点 A , B , C , D 分别向 B , C , D , A 的方向截取相等的线段 AP , BQ , CR , DS 。连接PQ , QR , RS , SP ,成一个正方形 PQRS 。要使这个正方形的面积最小,这四条线段应该怎样截取?

2.在半径是20厘米的圆内作一个内接矩形。这个矩形的面积最大可以是多少平方厘米?

3.有长200米的篱笆,要把它围一块矩形园地,问围成的园地面积最大是多少?
*4.一个窗户的形状是矩形再加上一个等边三角形,如果窗户的周长是6米,
(1)求窗户面积 y (平方米)与等边三角形边长x(米)间的函数关系;
(2)怎样才能使透射进室内来的光线最充足?
下期预告:
§4.6利用二次函数的图象解一元二次方程
我们来观察二次函数 y =x²-2x-3=( x -1)²-4的图象

(图4.18).
这条抛物线交x轴于两点
A (-1,0), B (3,0).
这就是说,当 x =-1或者x=3的时候,函数 y=x²-2x-3的值是0.换句话说,也就是
x =-1和 x=3是方程
x²-2x-3=0
的两个根.
这个例子告诉我们,解一个一元二次方程......
上期链接:https://m.toutiao.com/is/iM2v9UYC/ - 百科漫谈:名师彻底讲透初等函数(18)二次函数的性质 - 今日头条
