从变换方程开始。

逆变矢量是一个具有上标的对象，其分量在坐标变换下进行如下变换：

方程1

1-形式是一个具有下标索引的对象，它的分量在坐标转换下进行如下转换：

方程2

两个方程都描述了坐标变换。方程1告诉我们如何在一个逆变向量上进行坐标变换，方程2告诉我们如何在1-种形式上进行坐标变换。

是开始时逆变矢量的分量，在坐标系

中表示

是最后得到的逆变矢量的分量，在坐标系

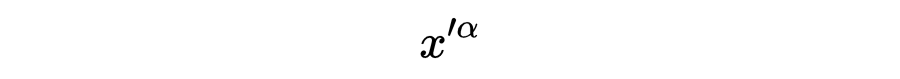
中表示

是开始时1-形式的分量，在坐标系

中表示

是最后得到的1-形式的分量，在坐标系

中表示

而

描述了新旧坐标系之间的关系。具体地说，我们求函数的偏导数将一个系统的坐标与另一个系统的坐标联系起来。这些项代表了一个变换矩阵。我们用正确的变换矩阵乘以旧坐标系中的向量得到新坐标系中的向量。

我们现在来看看1-形式和逆变向量的具体例子

1-形式

想象一个充满流动空气的房间。在开着的窗户或暖气片上方，空气可能流动得更快，而在角落或书架后面，空气流动得更慢。我们可以测量房间里每一点空气的速度，我们可以用房间的x，y， 坐标来表示速度。

我们现在考虑标量场T的梯度

在房间里的某个特定地点。

我们现在可以说，标量场的梯度▽T是1-形式的例子。

让我们问问自己，如果我们想把梯度（1-形式）转换成球极坐标会发生什么？在这种情况下，我们需要把T(x, y, z)变成一个不同的函数

该函数根据球面极坐标r， θ，φ给出温度。这两个函数是不一样的，因此我们可以说

其中

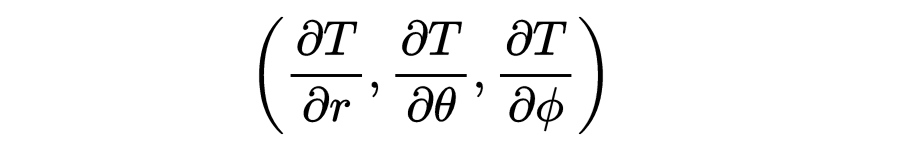
是球坐标中▽T的分量。

方程2告诉我们1-形式的定义是

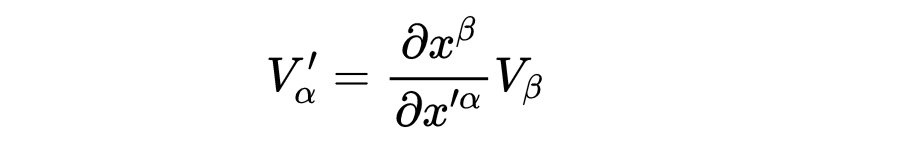
可以把它写成

如上所述

表示一个转换矩阵，在本例中是一个3 × 3转换矩阵，因为有三个β坐标x、y、z和三个α坐标r， θ， φ。

我们可以把这个神秘的变换矩阵表示为

如果我们知道这个矩阵的元素我们可以用1-形式乘以它，找到新的1-形式。

很快就会看到，我们通过对一个系统中的坐标与另一个系统中的坐标相联系的函数求偏导数来找到变换矩阵的元素。所以

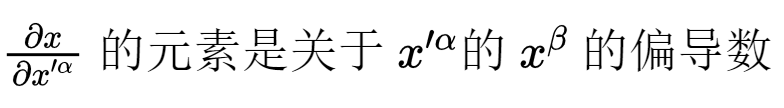
例如，元素

可以计算如下

其中，r，θ，φ都是x，y，z的函数。以类似的方式，我们可以计算其他元素。现在不要担心具体怎么做的细节，只要试着理解为了把一种形式的分量从一个坐标系转换到另一个坐标系，我们需要一个变换矩阵。

逆变向量

我们现在假设房间里每一点的空气以速度V运动，V是笛卡尔坐标x，y，z的函数。

我们可以用时间t来参数化运动粒子的路径，从而得到一个矢量，它的分量表示物体在x，y，z方向上的空间速度（或三维速度）。粒子的空间速度是路径的切线矢量，并且有分量

我们称这个向量为

我们现在可以说速度矢量是逆变矢量的一个例子。

再一次假设我们要把这个向量从笛卡尔极坐标变换到球极坐标，方程1告诉我们逆变矢量的定义是

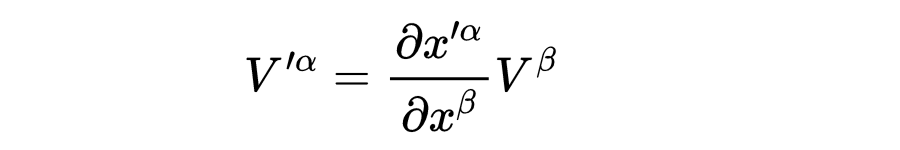
与1-形式一样，我们通过对一个系统中的坐标与另一个系统中的坐标相联系的函数求偏-导数来找到变换矩阵的元素。

利用上面的例子，在四维时空的背景下，我们现在可以给出逆变矢量和1-形式的定义。

定义逆变矢量

逆变矢量量是时空中参数化曲线的切矢量。如果曲线的参数是λ，使用一个坐标系，切线向量是

这条曲线的一个相对论例子可能是一个粒子在时空中运动的世界线，而在这条曲线上的一个逆变矢量的例子可能是粒子的四维速度

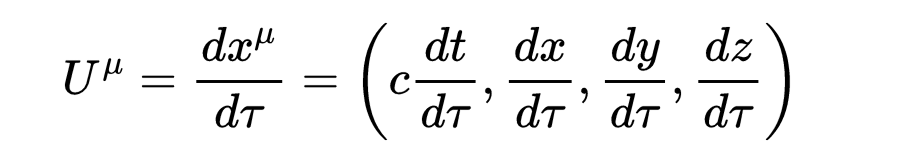
设c=1，四维速度变成

其中四维速度定义为粒子的四个位置（t, x, y, z）相对于固有时的变化率，固有时是曲线上的参数。

定义1-形式

考虑一个标量场，其中ϕ是

（例如，β = 0,1,2,3 = t, x, y, z）的标量函数，并且在洛伦兹变换下是不变的（意味着对于时空中的每个点，它在所有惯性系中具有相同的值）。标量场在坐标系中的梯度为

其中：

是1-形式具有分量：

以上就是逆变向量和1-形式的基本内容。这里就不再更进一步看变换矩阵是如何构造的了，因为在处理张量时，你不需要做这些计算——数学只是张量代数规则有效的原因。