提到最美丽的方程，很多人首先想到的可能是欧拉恒等式，

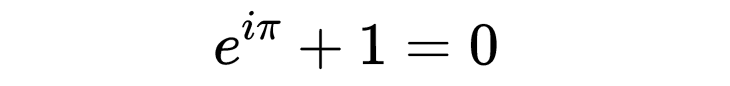
它是复分析中建立三角函数与复指数函数之间基本关系的数学公式。物理学家理查德·费曼称这个方程为“我们的宝石”和“数学中最卓越的公式”。数学中还有一个非常美丽的公式，但鲜为人知，它就是黎曼函数的函数式方程（Riemann’s Functional Equation）。

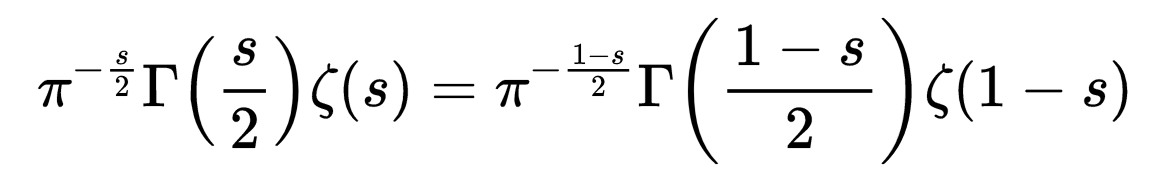
在本文中，我将推导上述方程并了解其组成部分。为此，我们需要从更容易理解的地方开始。

什么是对称？简单说，一个物体（比方说一只花瓶或一张脸），如果从不同的角度去看，或者从镜子里看，它的样子保持不变，那么我们就说这个物体是对称的。但怎样才能把这种说法精确化呢？从不同的角度去看，它的样子保持不变，这句话的确切含义是什么呢？想象在你面前有某个物体，这个物体绕某一条直线或某一个点旋转了一下。这样操作之后，这个物体的样子是否与原来相同？如果相同，我们会说这个物体对于这种操作来说是“对称”的。例如，取一个圆，让它绕其圆心随意地旋转任何一个角度，结果得到的图形都与它开始时的图形完全相同。

方程也可以有对称性。在等式中

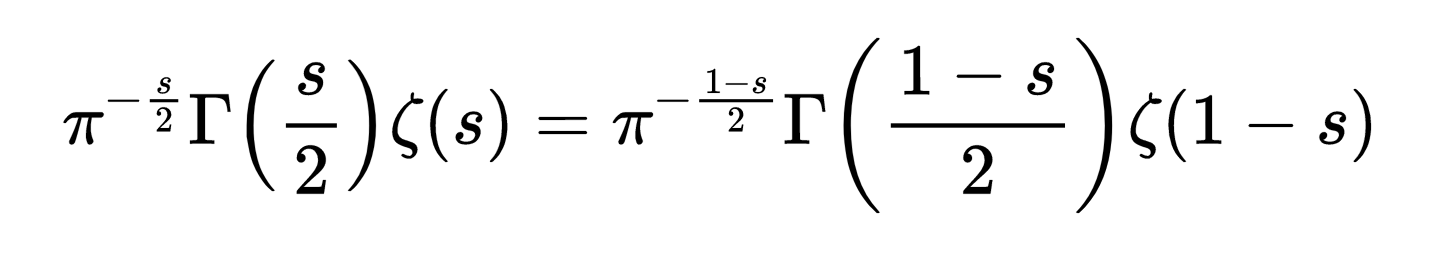
我们称左边为Λ(s)。这个方程表明Λ(s) = Λ(1-s)。也就是说，通过用1-s替换s，我们“回到了起点”。这是反射对称。所以黎曼函数式方程是关于对称性的。更值得注意的是。这个方程显示了Gamma函数和黎曼zeta函数之间的关系。

Gamma函数

Gamma函数是数学中最重要的函数之一。从统计学和组合学到数论和物理学，gamma函数无处不在。它是由反常积分定义的，

其中z为Re(z) >0的复数。

Re（z）表示复数z的实部。

Gamma函数有自己的几个函数式方程（functional equations），如

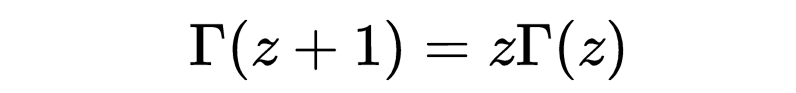
如果n是一个自然数，那么Γ(n) = (n-1)!，例如Γ(5) = 4!= 4⋅3⋅2⋅1 = 24。通过解析延拓，我们可以理解复平面上的Gamma函数，除了有单极点的非正整数。Gamma函数还有其他与之相关的重要的函数式方程，例如，著名的欧拉反射公式，

zeta函数

黎曼ζ函数是解析数论的明星。这个函数的零点的分布与素数的分布相关，因此我们对这个函数有极大的兴趣。

当复数s的实部大于1时，我们可以用无穷级数来定义zeta函数，

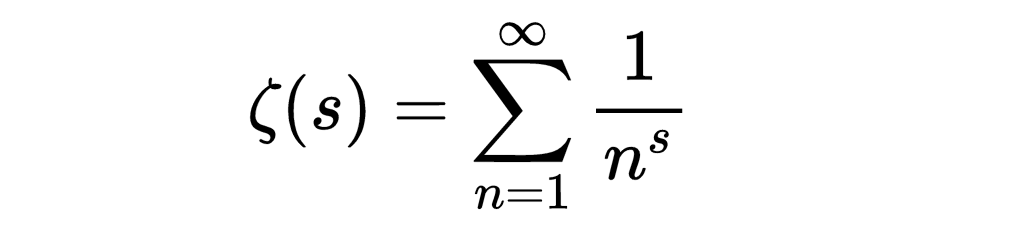
当Re(s) < 1时，我们需要通过解析延拓得到另一个定义。它与质数的联系通过它的欧拉乘积表示为质数的乘积就很清楚了，

泊松求和公式

这个公式值得专门写一篇文章。这个定理指出

右边的和是f的傅里叶变换在整数上的值。让我们定义一个well-behaved函数f的傅里叶变换为积分，

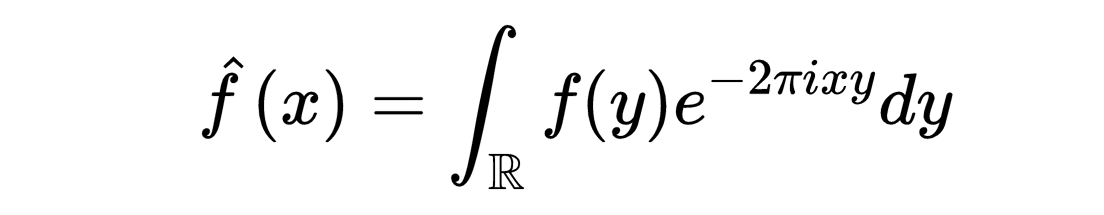
这里的符号表示积分是从负无穷到正无穷。我们简短地来证明泊松求和公式，我们只需证明下面等式即可，因为设x = 0就得到了上述公式，

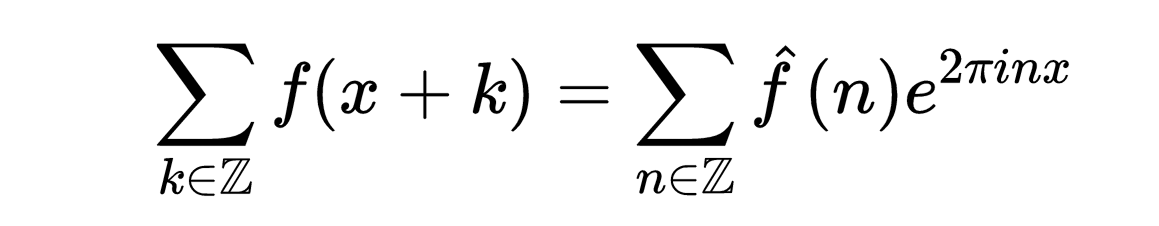
首先，设f是一个具有定义良好的傅里叶变换的函数。然后，我们定义一个函数F

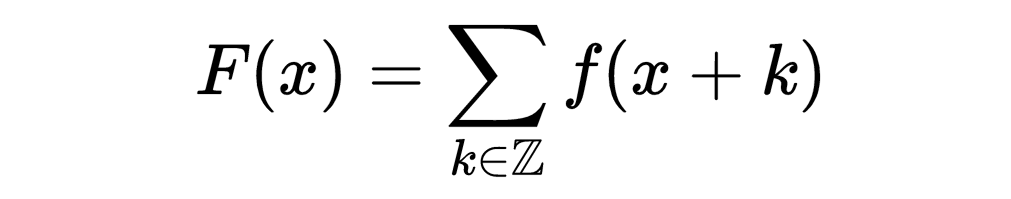
显然，这个函数是有一个周期的周期函数，这意味着它有一个傅里叶级数。计算F的傅里叶系数，我们得到

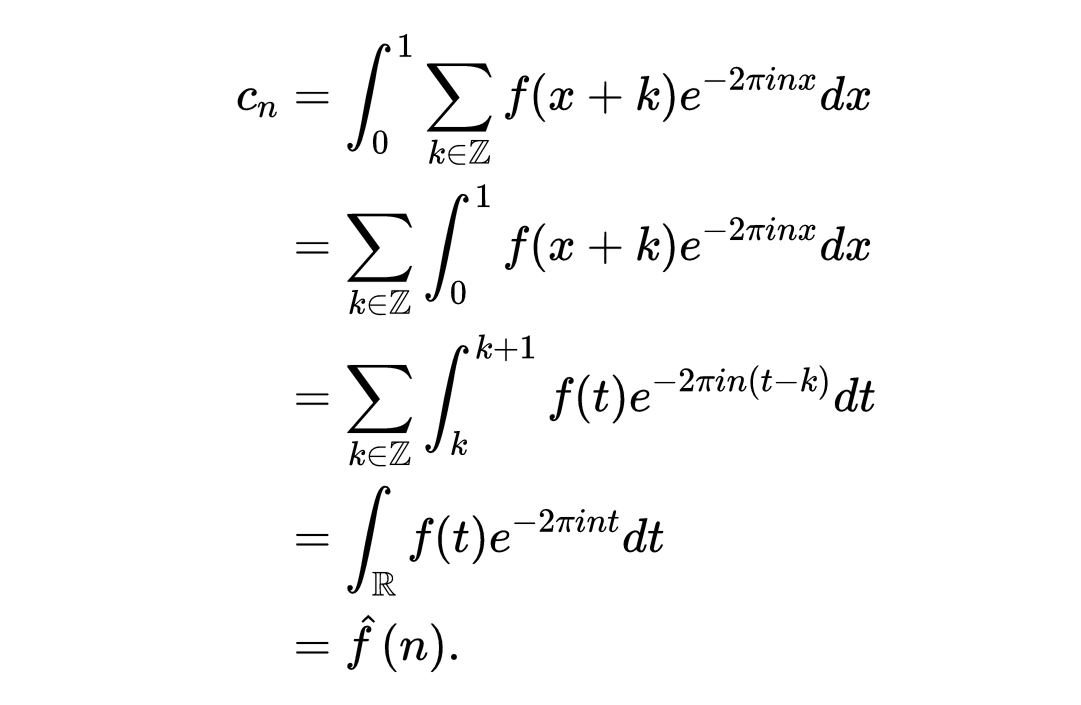
现在，我们知道F等于它的傅里叶级数

这就是我们想要证明的。

Theta 函数

有一类重要的函数叫做雅可比函数。我们只需要研究其中的一个——最简单、最经典的一个。在本文中，我们用实函数来定义theta函数

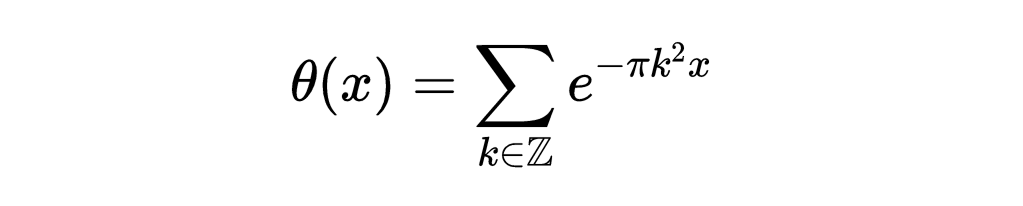
请注意，k在整数上运行，因此也可以写成自然数上的级数，

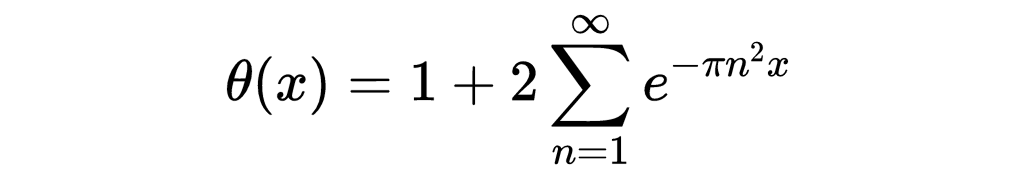
我们把左边的级数称为ψ(x)，

在这种情况下，有一个简单的关系θ(x) = 1 + 2 ψ(x)。这个函数的关键特征之一也是一个函数方程。这个函数是满足的

为了证明这一点，我们将使用泊松求和公式。第一步是将下面的积分塑造成更易于处理的东西。我们有

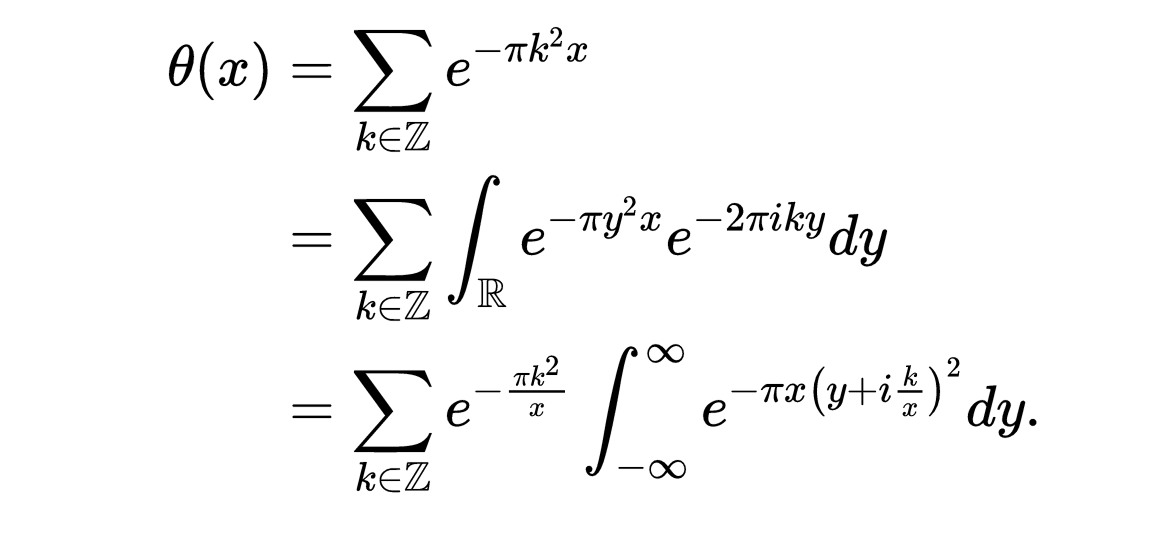
看级数中的积分，我们可以做一个替换把它看作是复平面上的围线积分。然后我们可以用柯西积分定理来证明它实际上等于沿着实线上平行路径的积分。由此得到的高斯积分是一个经典的高斯积分，在数学中随处可见。也就是说，

把这个结果放到函数的泊松求和公式中，我们得到了想要的结果。这意味着，

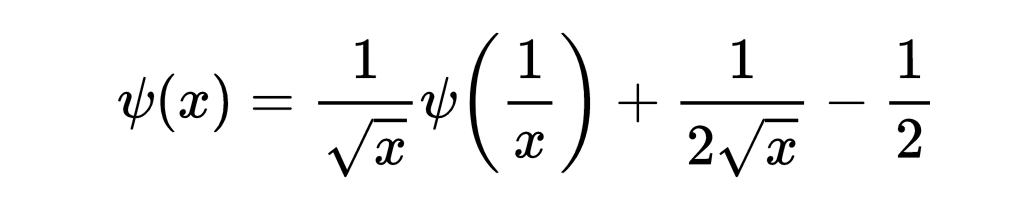
现在，我们将使用已经建立的工具来证明函数方程，

首先，我们用替换的形式来定义函数，用参数s/2来写它

其中我们需要Re(s) > 0，如上述定义。现在我们做如下替换

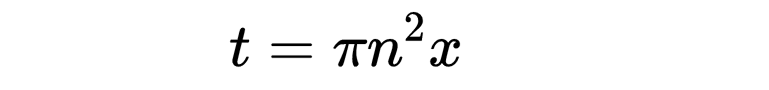
得到

因为这对所有的自然数都成立，所以我们可以把两边的所有自然数相加得到

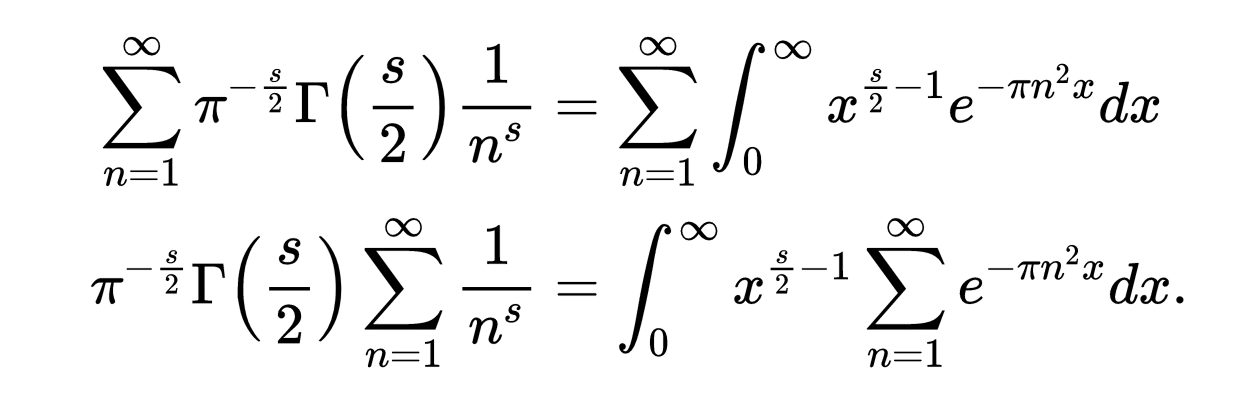
这就是上面的ζ函数和ψ函数。我们可以把它写成

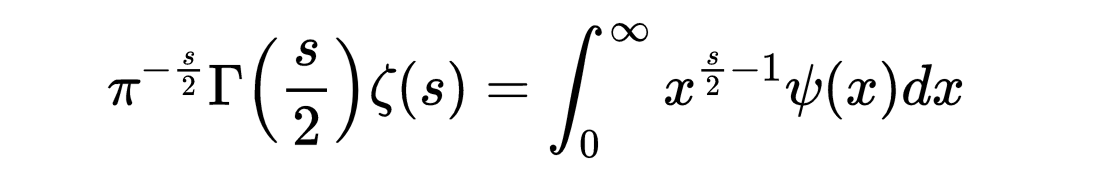
现在我们可以把积分拆分成两个区间然后利用ψ函数的变换性质，利用下面的性质，

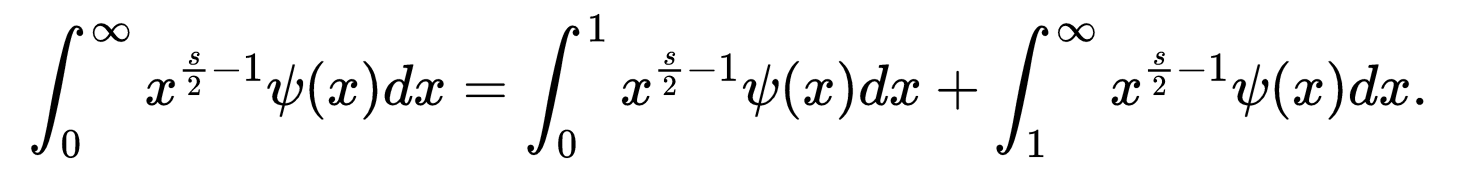
放大右边两个积分中的第一个，我们可以看到ψ的变换得到如下结果

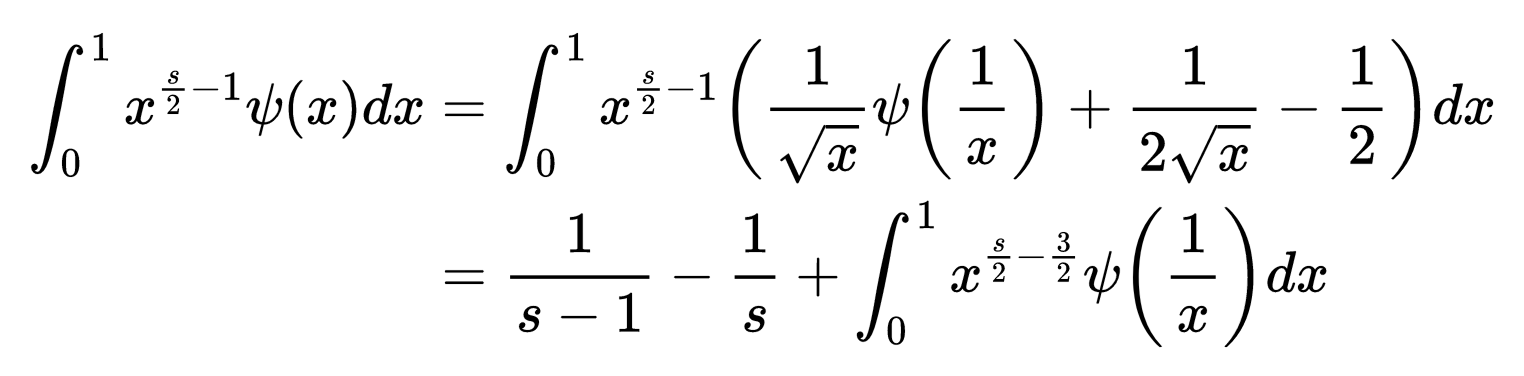
现在我们可以做一个简单的替换把两个积分合二为一。得到的积分是

注意，右边的表达式在s和1-s处的值是相同的。有时你会看到黎曼函数方程的形式略有不同。如果我们使用欧拉反射公式，我们可以得到一个正弦函数表示的因子

它清楚地表明黎曼ζ函数在负偶数上消失了，这要归功于正弦因子。它没有在正偶数上消失的原因是它遇到了一个来自函数的极点。

最后

zeta函数有许多紧密相关的“表亲”，叫做狄利克雷L函数。它们非常相似，最简单的函数就是黎曼zeta函数本身。它们都可以被定义为一个级数和一个欧拉积。他们满足

更详细的讨论超出了本文的范围，但看看与上面的黎曼函数方程的相似性。因子包含一个所谓的高斯和。关于这个一般结果的美妙之处在于，它适用于黎曼zeta函数以及上面提到的所有密切相关的表亲。

它们都有这种对称性，它们都被期望满足黎曼假设，即它们所有的非平凡零点都在对称线上。在zeta函数的情况下，对称线是垂直线Re(s) = 1/2，也称为临界线。