分数比较大小。题目呈现:
如下图所示,请选择“<”或“>”符号填入圆圈。

解法一:容易想到的是通分,当两个分数的分母相同时比较分子,分子大则分数大。
有的同学学习过速算,就想可以通分,把两个分数的分母都化为11×13。按照口诀,两边拉开,中间相加,所以11×13等于143。但是通分比较麻烦,有没有更好的办法呢?
当然有。可以统一分子,当两个分数的分子相同时,比较分母的大小,分母小的分数大。
于是有下面的解法:
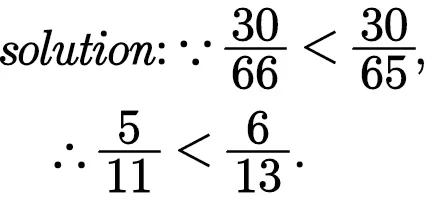
这个解法用到了商不变的原理。被除数和除数同时乘以或除以一个不为零的数,商不变。
某头条作者的解法如下图所示:

我坚信数学来源于生活。以上解法都是通过计算结果才能判断两个分数孰大孰小,那就是落了下乘。更好的办法就是用生活中的常识去判断,迅速得到答案。
举个例子。你用上面的题目考一个醉汉,他会回答不知道。你如果以为他真的不知道答案,那就是你肤浅了。因为你的问法不对。如果你想知道答案,要这么问:11个人喝5瓶酒和13个人喝6瓶酒比起来,哪种喝法更好?
醉汉会这样回答:当然是13个人喝6瓶酒更好啦。以我喝酒20多年的工龄打保票,相信我没有错的。
醉汉贪杯,他不假思索,凭直觉就知道这两个分数哪个更大,哪种喝法能够喝到更多的酒。
如果是我们,比如说我们平时滴酒不沾,不像醉汉是久经(酒精)考验的人,我们该如何判断这两种喝法哪种能够喝到更多的酒?
举个例子。设一瓶酒1000毫升,小圆桌有10个人,平分5瓶酒。而大圆桌有12个人,平分6瓶酒。显然,这两桌客人喝到的酒但是一样多,即每人都可以喝500毫升。请问,你如果想多喝酒,应该去哪一桌喝呢?
答案不言而喻。你拿着一个空杯,小桌上有10杯酒,你和这10人平均一下,喝到同样多的酒,假设喝a毫升。如果你拿着空杯去大桌,就是12杯酒,每一杯都和小桌一样是500毫升。你和这12杯平均一下,喝到同样多的酒,假设是b毫升。现在问你a和b两个数,哪个数更大?答案就像水晶一样透明,当然是a小b大啦!去大桌喝酒能够喝得多。
这都是很浅显易懂的道理,不用计算就知道哪个大哪个小。因为题目是填空题,比较大小,无需计算出每个分数的准确值,也不需要写出解题过程,所以可以用生活中的常识来快速判断大小。
有的同学好奇心很强,非要计算一下准确值,那就满足一下吧。请看下图:

5瓶酒分给11人喝,每人分到的酒,超过454毫升。算出来是循环小数,可以化为分数。而13人喝6瓶酒,每人分酒超过461毫升。而分配本来就是除法应有的题中之义。
科学尚未普及,媒体还需努力。感谢阅读,再见。








