
图片由AI创作
第一章
1.3优化素质
优化数学素质的主要途径是注重知识的发生过程,如概念的形成过程,定理的发现过程,证明的寻找过程等.对于解题来说,进行解题过程的分析是优化素质的一条捷径.
题目呈现
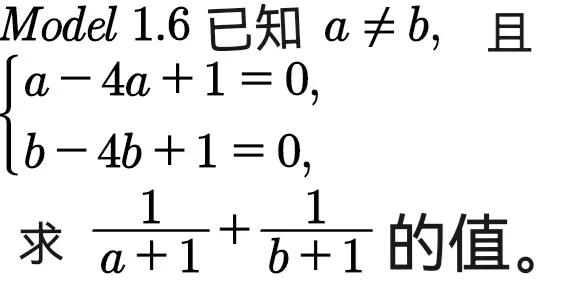
例1.6 已知 a ≠b,且
{a²-4a+1=0,
{b²-4b+1=0,
求

的值。
分析 由

可见,只须求出 a + b , ab 即可.又由已知得 a , b 是二次方程x²-4x+1=0的两个根,故有a+b=4, ab =1.
故得

这样,我们通过有理有据的分析找到了一个解题思路,也得出了正确答案.但是,学数学如果停留在这一层次上,仍有"进宝山而空返"的遗憾.当初我们不知道

的值是多少,探索具有一定的盲目性,走点弯路也在所难免,但找到

之后,情况就不一样了.多了这个信息,我们就有可能对问题看得更加透彻.就像爬山,一开始,我们不知道怎么走,见到能走的地方就走,但爬到山顶之后,往下一看,一切都清楚了,原来有更直、更平、更好的路。这个居高临下的回首,就为我们提供了指导性的经验.

事实上,由(1)知,

只须
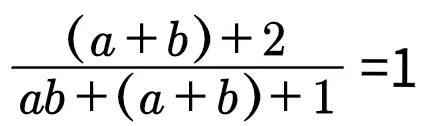
即(a+b)+2=ab+(a+b)+1,
即 ab =1.
由此可见,当初求"a+b=4"是多余的,有ab=1就够了.这一瞬间的恍然大悟,体现了数学的领悟.
解 由已知得 a , b 是二次方程
x²-4x+1=0的两个根,故有
ab =1,
从而

由于这种解法比较接近问题的实质,推广立即成为可能(见习题1第3题).
以优化素质为目的的解题过程分析,本书的第2章、第11章等处还要展开.事实上,上面的6个例子只是"怎样学会解题"的引言,本书的叙述,正是沿着这样的宗旨和思路,与读者一起去领略数学的内容,领会数学的方法,领悟数学的思想,培养数学的意识.
确实,谁也无法教会我们所有的习题,但是,我们可以通过有限道题的实践、分析与本质把握,去领悟那种能解决无限个问题的数学机智.
习题1
3.已知 abc =1.求证:

反之成立吗?
4.分析下题的解题过程,删去多余步骤,给出一个简化解法.
题目 已知二次函数
y=x²-mx+(m-2)的图像与 x 轴交于A ,B 两点,且|AB|=5/2.抛物线的顶点为C,求△ABC 的面积.

解 设 A , B , C 的坐标为 A (x₁,y₁), B (x₂,y₂), C (x₃,y₃),则x₁,x₂是二次方程
x²-mx+(m-2)=0
的两个根,故有
x₁+x₂= m ,
x₁x₂=m-2.
从而

得4m²-16m+7=0.
解得

从而抛物线为

或

两种情况下均有

所以,所求面积为125/64.
7. 实数a,b满足ab=1,记

则M,N的关系为
(A) M>N; (B) M=N; (C) M<N; (D) 不确定.
(1996年全国初中数学联赛试题)
第11章
为了更美的题解
——解题过程分析
11.1拉开黑房间的电灯
在例1.6中,我们一开始的分析,觉得应求出a+b=4, ab=1
来,但在获得解题思路之后回过头来一看,却发现求出
a+b=4是多余的.这就像黑夜中,我们走进了一座黑房间,不得不摸索前进,弄不好还会碰壁;但拉开电灯之后,一切都明明白白,房间内的结构和摆设一览无余.

在我们这里,"拉开电灯"就是"分析已经解过的题".在第2章我们曾专门分析过解题的信息过程,而本书各节的许多例子也无不伴随着"分析解题过程"的主旋律.这一次,我们将从优化解题过程的角度继续这种分析.
图11.1
让我们回过头来看看习题1第4题."电灯已经拉开",我们首先求出了两条抛物线

然后求出顶点 C 的纵坐标,经计算,两个顶点的纵坐标是相同的:

于是,两种情况下有等值的面积

无论我们怎么检查,都没有发现有任何错误:推理是严谨的,计算是准确的.
但是,数学是真与美的统一,因而,解题也应该既正确无误又艺术优美.这里说的美,主要不是指外在的、书写或绘图的工整规范,而是指在解题思想、解题方法、解题技巧上所体现的数学内在的统一美、对称美、简洁美和奇异美.
为了学会解题,为了通过解题来优化我们的思维素质,我们要"拉开电灯",睁大眼睛,分析解题过程.上述解题过程中有一个现象应该引起我们的思考:既然两条抛物线顶点有相同的纵坐标(注意,横坐标不相同),那么我们能否统一地一次求出y₃呢?
再分析解题目标,由面积公式

可知,为求面积只需求y₃,为求 y₃,先确定m只是充分的,并不必要.因为抛物线的纵坐标可以由 AB 的距离算出.由
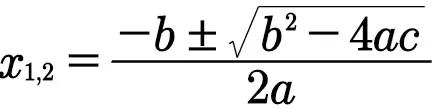
得

但

这说明,求 m 是多余的.
解题过程中存在多余的思维回路不仅不优美,而且还存在潜在的危险:
第一,干扰正确思路的寻找,有时还会产生误导.
第二.即使不误导,万一在计算过程中出现差错,也会前功尽弃。
对比一下就可以看到,直接由式(1)得出 y₃,再代入面积公式,书写量只是原解法的⅓,计算也不易出错.更重要的是,我们的解题能力已经在这种再回顾的潜移默化中获得了很大的提高.
11.2 如何分析解题过程
解题经验告诉我们,进行下述四个方面的分析,将有助于寻找更美的数学解.
(1)看解题过程多走了哪些思维回路,通过删除、合并来体现简洁美.
(2)看能否用更一般的原理去代替现存的许多步骤,以提高整个解题的观点和思维的层次.
(3)看能否用更特殊的技巧去代替现有的常规步骤,以体现解题的奇异美.
(4)看解题过程是否浪费了更重要的信息,以便开辟新的解题通道.
一般说来,当我们面对一个尚待解决的问题时,总是先瞄准某些已经抓住的方向,展开大跨度、粗线条的联想或类比,力求以破竹之势直达解题目标.这时候的"脑风暴"无暇顾及更多的细节,也来不及选择更平坦的道路,但是当思路一旦打通,题目初步解出时,兴奋(第一次兴奋)之余的沉思,将会使我们冷静地找回当初浪费在半途上的更重要的信息,将会使我们洞悉那本来不需要的许多思维回路,进一步的思考,更周密的运筹,常常会激发出一个更机智的数学念头,这时候的兴奋(第二次兴奋)不仅较前次更为强烈,而且更充满美感.
以下略。

《数学的领悟》截图
文章来源《数学的领悟》,作者罗增儒教授。
