全文约2200 字;
阅读时间:约6分钟;
听完时间:约12分钟;

小胡在一家家电工厂的PMC部门工作,最近他感到非常苦恼,因为工厂近期上线的产品都遇到了无法齐套生产的问题。不论是产品A还是产品C,要么缺少物料1,要么缺少物料2,总是无法凑足订单所需的数量,比如1000套。有时候一种物料可能有充足的库存,如1500件,而另一种物料却只有600件。
面对这种情况,小胡有两个选择:一是等待所有物料齐套后再开始生产;二是调整生产计划,确保能够根据现有物料进行最小齐套生产。例如,对于1000套A产品的订单,可能只能先生产300套;或者对于2000套B产品的物料,也只能先生产200套。
由于客户坚持要多少就得供应多少,小胡不得不采取最小齐套的方式来生产。然而,由于很多物料是共用的,确定最小齐套数量成了他最头疼的问题。如果只需要生产单一产品,排查起来还算容易,但现在需要同时处理多种产品的生产需求。小胡想知道是否有快速排查的方法来解决这个问题。
 最小齐套
最小齐套要解决这个问题,需要先了解什么是最小齐套?
在离散制造过程中,“最小齐套”是指根据现有最少物料的数量来确定能够生产的最小完整产品数量,以确保每一套产品都是完整的且可以正常销售或使用,这是一种优化生产计划、提高效率和减少浪费的策略。
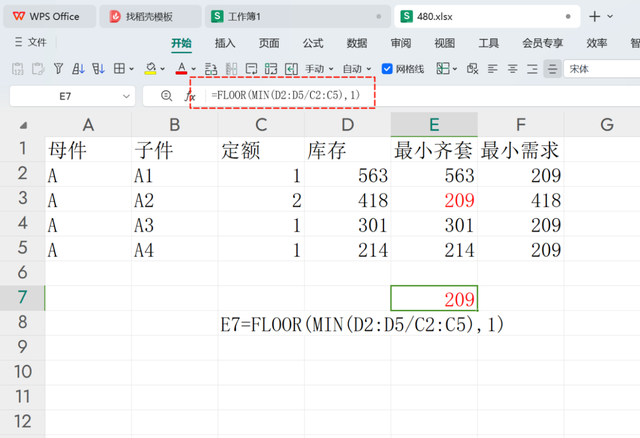
举例说明,下图中,母件A由4个零件组成(A1/A2/A3/A4),每个零件对应的定额分别为{1;2;1;1},库存为:{563;418;301;214},此时录入以下公式:
E7=FLOOR(MIN(D2:D5/C2:C5),1)
公式解释:
D2:D5 表示零件A1到A4的库存量。
C2:C5 表示零件A1到A4的定额数量。
MIN(D2:D5 / C2:C5) 计算每个零件的实际可用数量(库存除以定额),然后找出这些比例中的最小值。
FLOOR(..., 1) 确保计算结果向下取整到最接近的整数,从而得到可以生产的最小齐套数量。结果为:209
代表A母件可以生产209套。效果如下图所示:
 资料准备
资料准备如果是针对单一产品的最小齐套计算,其产品逻辑和公式设计都非常简单易懂。但如果是涉及多个产品的计算,则会变得较为复杂。这时,需要准备的资料也会增多,包括产品BOM表、产品MPS生产主计划、子件库存表、产品分解表以及产品库存扣减表等。
为了帮助大家快速理解多产品的最小齐套判断,这里我们用三个产品A、B、C来模拟多产品的齐套判断。首先,我们需要建立三个表格。其中第一个表格为产品MPS主生产计划表,A列列出产品名称,即需要生产的母件;B列则留空,用于填写后续通过公式计算得出的最小齐套生产数量。

表2:产品的BOM物料清单表,这张表是子件分解的核心,也是判断最小齐套的关键。其格式为:A列为母件,B列为子件,C列为定额。这是一张标准的一维母子件格式的BOM清单。

表3:设计为库存明细表加分解表。A列为产品名称,B列为当前库存量,C列为第1次扣减量,D列为第2次扣减量,以此类推。根据需要计算多少个产品的最小齐套量,就预留相应数量的列来进行扣减。
 开始计算
开始计算整理好上述三张表后,就可以开始计算了。计算的工作量取决于产品的数量,产品数量越多,计算量越大。首先,我们设计第一个产品的算法。新建表4作为分解表,在A到G列分别录入以下标题:“母件”、“子件”、“定额”、“库存”、“最小齐套”、“最小需求”和“剩下库存”。接下来,分别录入以下公式:
A2=INDEX(FILTER('2.BOM'!A:C,'2.BOM'!A:A='1.MPS'!A2),,1)
B2=INDEX(FILTER('2.BOM'!A:C,'2.BOM'!A:A='1.MPS'!A2),,2)
C2=INDEX(FILTER('2.BOM'!A:C,'2.BOM'!A:A='1.MPS'!A2),,3)
D2=XLOOKUP(B2#,'3.库存'!A:A,'3.库存'!B:B)
E2=FLOOR(D2#/C2#,1)
F2='1.MPS'!B2*C2#
G2=D2#-F2#
以上公式解释:
A2: 使用INDEX和FILTER组合查询与产品A相关的子件信息,返回子件名称。
B2: 返回该子件的定额数量。
C2: 返回子件的定额数量。
D2: 使用XLOOKUP函数查询子件B2在库存表中的库存量。
E2: 计算该子件的实际可用数量(库存除以定额),并向下取整。
F2: 计算产品A的最小需求量(即产品A的最小齐套生产数乘以子件的定额)。
G2: 计算子件的剩余库存量(即库存量减去最小需求量)。

这里计算出产品A的最小齐套是212后,切换到表1,在产品A对应的B列录入公式:
B2=FLOOR(MIN('4.分解'!E2#),1)
公式解释:
这个公式计算了产品A所有子件的最小齐套数中的最小值,即产品A能够生产的最小齐套数量。
接下来就是重复第二个产品,继续在I到O列录入标题:“母件”、“子件”、“定额”、“库存”、“最小齐套”、“最小需求”和“剩下库存”。继续录入以下公式:
I2=INDEX(FILTER('2.BOM'!A:C,'2.BOM'!A:A='1.MPS'!A3),,1)
J2=INDEX(FILTER('2.BOM'!A:C,'2.BOM'!A:A='1.MPS'!A3),,2)
K2=INDEX(FILTER('2.BOM'!A:C,'2.BOM'!A:A='1.MPS'!A3),,3)
L2=XLOOKUP(J2:J5,'3.库存'!A2:A9,'3.库存'!C2#)
M2=FLOOR(L2#/K2#,1)
N2='1.MPS'!B3*K2#
O2=L2#-N2#
公式解释:
原理基本一样,注意库存引用这里是引用库存的C列,也就是扣减完产品A后的库存。

切换到表3库存表中,把表4分解A产品后,也就是扣减完最小齐套212套后的库存引用过来,录入以下公式:
=IFNA(XLOOKUP(A2:A9,'4.分解'!B2:B5,'4.分解'!G2#),B2:B9)

后面就是不断的重复,等所有的产品都进行分别扣减后,就计算出所排程MPS的最小齐套数量了。如下图所示:
 最后总结:
最后总结:小胡在面对多产品最小齐套问题时,通过合理规划和利用Excel公式实现了高效的解决方案。首先,明确了最小齐套的概念,即根据现有最少物料的数量来确定能够生产的最小完整产品数量,确保每一套产品都是完整的且可以正常销售或使用。接着,通过实例演示了如何利用Excel中的FLOOR和MIN函数结合物料清单(BOM)和库存数据来计算单一产品的最小齐套数量。
为了处理更复杂的多产品情况,小胡准备了一系列关键资料,包括产品BOM表、MPS生产主计划、子件库存表、产品分解表以及产品库存扣减表。通过创建专门的分解表,逐一计算每个产品的最小齐套数量,并通过Excel中的INDEX、FILTER和XLOOKUP函数来查找和更新数据。计算完成后,通过在库存表中应用XLOOKUP函数,将每次计算后更新的库存量引用过来,实现对库存的动态跟踪。
最终,通过不断重复这一过程,小胡能够准确计算出所有排程产品的最小齐套数量,有效地解决了多产品最小齐套问题,提高了生产计划的灵活性和准确性。这种系统化的方法不仅简化了计算流程,还提高了生产效率,确保了能够及时响应客户需求的同时减少物料浪费。
