全文约2507字;
阅读时间:约7分钟;
听完时间:约12分钟;

在编制生产计划的过程中,生产计划员通常需要安排多条生产线的调度。这涉及到计算每条生产线具体的开工时间和预计完工时间。进行这些计算时,关键因素包括:生产线的数量、统一规定的开工时间以及各个产品对应的标准工时。基于上述信息,可以利用特定公式快速准确地确定每条生产线的开工和完工时间。
 整体思路
整体思路在确定了统一的开工日期(9月30日)之后,接下来需要单独计算每条生产线的具体开工时间和完工时间。这一过程的核心步骤是首先识别出每条生产线上安排的产品。一旦明确了这些产品,就可以根据它们各自的标准工时来计算总的所需工时,并将这个总工时转换为“天”的形式,以便与9月30日这一基准日期进行运算。
例如,如果计算得出某条生产线所需的总工时换算成0.8天,则从9月30日起加上这0.8天即可得到该生产线的预计完工时间。值得注意的是,在连续的任务安排中,一个任务的完成时间即为下一个任务的开始时间。
为了实现上述目标,可以通过以下步骤操作:
筛选每条生产线上的产品。
根据筛选出的产品及其标准工时累加总工时。
将累计工时转换为以“天”为单位的形式。
使用垂直堆叠函数处理所有生产线的开工时间数据。
从上一步骤的结果中移除最后一行的数据后,将其余部分与相应的开工时间相加,从而得到每条生产线的实际完工时间。
整个流程可以概括为:筛选产品 -> 累计工时 -> 转换天数 -> 计算开工时间 -> 计算完工时间。
筛选线体如果采用传统的公式方法,上述流程其实可以大大简化。但为了实现完全动态化的数组处理,这里采取了一系列较为复杂的步骤来设计表格。首先,我们需要筛选出特定线体对应的标准工时。为便于理解,下面将分步展示如何编写相关公式。
=FILTER(M5#,G5#="1#")
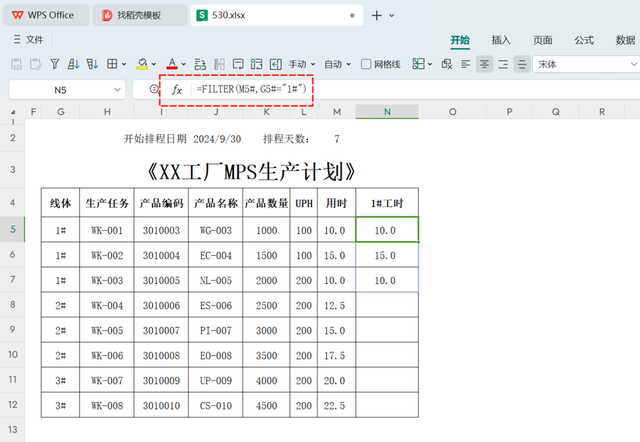
公式解释:
参数1(数组): M5# 表示每张生产任务所需的标准工时。
参数2(条件): G5# 代表每张生产任务对应的生产线编号;在此处我们设定条件为 "1#",意味着只选择那些属于第一生产线的生产任务的标准工时数据。
通过这种方式,我们可以轻松地获取到指定生产线上的所有相关标准工时信息,为进一步计算开工时间和完工时间打下基础。
累计天数第二步是将筛选出的工时进行累加。在累加之前,需要先将这些工时转换为天数格式。由于只上白班(即每天工作12小时),我们将标准工时除以12来完成单位转换。然后,使用SCAN函数对转换后的数据进行累计求和。以下是具体的公式:
=SCAN(0,FILTER(M5#,G5#="1#")/12,SUM)

公式解释:
参数1(初始值): 0,作为累加的起始值。
参数2(数组): FILTER(M5#, G5#="1#")/12,这里首先通过FILTER函数筛选出第一生产线的所有生产任务的标准工时,然后将每个工时除以12转换为天数。
参数3(累加函数): SUM。每次迭代中,将当前累计值与新值相加。形成累计求和的效果。
这样,我们可以得到一个包含每一步累计工时(以天为单位)的结果数组,便于后续进一步计算开工时间和完工时间。
开工时间第三步是计算每条生产线的开工时间。给定的统一开工日期是9月30日,这个信息由生产计划员在单元格J2中录入。我们需要将这个日期与筛选出的第一生产线(1#)的标准工时累加后的天数进行垂直拼接,然后去掉最后一行的结果,从而得到每张生产任务的实际开工日期。以下是具体的公式:
=DROP(VSTACK(J2,J2+SCAN(0,FILTER(M5#,G5#="1#")/12,SUM)),-1)

公式解释:
VSTACK(J2, ...): 将J2单元格中的日期(即9月30日)与后续计算出的每个累计天数相加后的日期垂直堆叠。
J2 + SCAN(..)):
FILTER(M5#, G5#="1#")/12:筛选出第一生产线的所有生产任务的标准工时,并将其转换为天数。
SCAN(...):对这些天数进行累加,每次累加都将当前累计值加上新的天数值
J2 + ...:将初始日期9月30日与累加后的天数相加,得到每个生产任务的实际开工日期。
DROP(..., -1): 去掉结果数组的最后一行,因为最后一行是最后一个生产任务的完工时间,而不是下一个任务的开工时间。
通过上述步骤和公式,我们可以得到一个包含每张生产任务实际开工日期的列表。
水平堆叠最后一步就是用函数REDUCE进行垂直方向堆叠,把不同线体筛选后的数据全部堆叠起来。录入动态数组公式:
=LET(J,J2,G,G5#,DROP(REDUCE("",UNIQUE(G),LAMBDA(X,Y,VSTACK(X,VSTACK(J,DROP(J+SCAN(,FILTER(M5#,G=Y),SUM)/12,-1))))),1))

公式解释:
LET 定义:
J 代表单元格 J2 中的统一开工日期(9月30日)。
G 代表列 G5#,其中包含了每张生产任务对应的线体信息。
UNIQUE(G): 提取出所有唯一的生产线编号。
REDUCE 函数:
初始值为一个空字符串 ""。
对于每个唯一的生产线编号,执行以下操作:
FILTER(...): 筛选出属于当前生产线的所有生产任务的标准工时。
/12: 将标准工时转换为天数。
SCAN(0, ...): 对转换后的天数进行累加求和。
J + ...: 将初始日期加上累计天数,得到每个生产任务的实际开工日期。
DROP(..., -1): 去掉最后一个累计天数,因为它对应的是完工时间而不是下一个任务的开工时间。
VSTACK(J, ...): 将初始日期与计算出的开工日期垂直堆叠。
VSTACK(, ...): 将当前结果与之前的结果垂直堆叠起来。
DROP(..., 1): 去掉最终结果数组的第一行,因为第一行是一个空字符串(REDUCE的初始值),不需要显示。
通过上述步骤和公式,我们可以将所有生产线的开工日期进行垂直堆叠,并生成一个包含每张生产任务实际开工日期的列表。这样可以方便地查看和管理不同生产线的任务安排。
同理也可堆叠出过完工日期:录入对应公式:
=LET(J,J2,G,G5#,DROP(REDUCE("",UNIQUE(G),LAMBDA(X,Y,VSTACK(X,J+SCAN(,FILTER(M5#,G=Y),SUM)/12))),1))

至此,一个全自动的主生产计划(MPS)排程表模型已经设计完成。由于采用了全动态数组公式,无需手动填充公式,这大大提升了生产计划员的工作效率。
最后总结通过上述步骤,我们成功构建了一个全自动的主生产计划(MPS)排程表模型。该模型利用了Excel&WPS中的全动态数组公式,能够自动计算每条生产线的具体开工时间和完工时间,从而极大地简化了生产计划员的工作流程。具体来说,整个过程包括筛选产品、累计工时、转换为天数、计算开工时间以及计算完工时间等关键步骤。
采用这种动态化处理方式的优势在于:
提高效率:无需手动填充或调整公式,减少了人为错误的可能性,同时节省了大量时间。
灵活性强:当生产数据发生变化时,只需更新基础数据,所有相关计算将自动更新,确保计划的实时性和准确性。
易于维护:一旦模型建立完成,后续的维护工作变得相对简单,生产计划员可以更专注于其他重要任务。
可视化管理:生成的排程表清晰地展示了各生产线的任务安排,便于管理层进行监督和决策。
总之,这个全自动MPS排程表模型不仅提高了生产计划的编制效率,还增强了对生产过程的控制与管理,是现代制造业中不可或缺的工具之一。通过这样的自动化解决方案,企业可以更好地应对市场变化,优化资源配置,提升整体运营效率。
