蒙特卡洛法是利用随机性来解决物理学、经济学、数学等多个领域的问题。如果运用得当，随机性可以为确定性问题提供比较完美的结果。

这篇文章，我将使用蒙特卡洛法来近似一些积分的值，这些积分不能用解析方法计算。有些积分的计算很简单，比如

那么如果是下面的积分呢

这时，我们可以用蒙特卡洛法近似这个积分的值。为了理解蒙特卡洛积分的原理，我们需要先了解大数定律。

大数定律

假设一位健身教练遇到了一个问题，他需要确定一个班级中所有学生的平均体重。假设这个班的人数是100人，所有的学生都是18岁。开始测量时，她从班上随机挑选5名学生，测量他们的体重并取平均值。

我们知道100个学生的平均体重是57公斤，但是健身教练不知道。

这5名学生的平均体重为45公斤，这对于整个班级的平均值而言要轻了不少。因为随机挑选的这5个学生的体重都过轻，他们的平均体重并不能很好地描述（代表）整个班级学生的平均体重。

于是教练重新挑选学生，但这一次，他不是随机选择5个学生，而是15个学生。他们的平均体重是67公斤。根据她的经验，她怀疑这个平均值不具代表性。她分析了这15名学生的锻炼情况，发现大约有10名学生缺乏体育锻炼，体重超标。然而，15个学生的平均体重更接近整个班级的真实平均体重。

让我们用数学方法来模拟这个问题。假设X_n是随机选择的n个学生的体重的集合，称为样本。X_n上方的横杠表示这些体重的平均值。下面是X_4的一个例子，

用μ表示所有学生的平均值，称为总体平均值。当增加n的值（从5、15到50）时，随机选择的一组学生的平均值，称为样本平均值，

随着n的变大，样本平均值接近总体平均值

因此，当样本数量增加时，样本均值收敛于总体均值。这就大数定律是告诉我们的。

大数定律的数学定义

设X_n是一个由n个独立同分布的随机变量组成的序列。

独立的意思是，n个随机变量是独立事件（在概率中），也就是说一个随机变量的出现不会影响其他随机变量的出现。

同分布的意思是，n个随机变量遵循一个概率分布分布。每个随机变量的期望值服从相同的概率分布，用μ表示，

所有的随机变量都属于同一个分布，因此有相同的期望值。

X_n（带横杠）同样表示样本的均值，

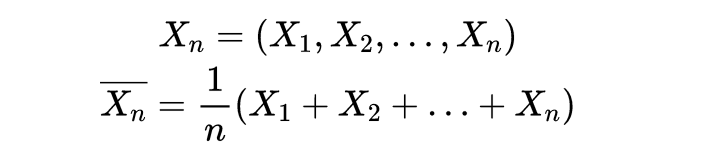
根据大数定律，

随着样本容量n的增加，样本均值接近整体均值

我们可以通过可视化的方式观察样本均值是如何接近理论均值的。在投掷均匀骰子的实验中，理论平均值为3.5，下面是实验结果。

蒙特卡洛法与数值积分

正如前面提到的，蒙特卡洛法使用随机性来解决确定性问题。基本方法是，在一个特定的域中生成随机数，对它执行一些确定性的计算。它在许多领域都很有用，比如物理学、经济学、工程学等。现在，我们将看到它在数学中的应用——用它来计算数值积分。

给定一个函数g，它的积分区间是[a, b]。我们的目标是用蒙特卡洛法计算这个积分。如果g是非初等函数，将其积分写成初等形式是不可能的。

初等函数是由幂函数、指数函数、对数函数、三角函数、反三角函数与常数经过有限次的有理运算（加、减、乘、除、有理数次乘方、有理数次开方）及有限次函数复合所产生，并且能用一个解析式表示的函数。

下面是一个非初等函数的例子，

考虑一个有n个随机变量的序列，服从均匀分布（uniform distribution），

注意均匀分布中的数字a和b，它们是函数g的积分范围。我们将函数g应用到所有这些随机变量上，

对于某连续随机变量Y，g(X_n)的理论均值（期望值）表示为：

连续随机变量Y的期望值

由于g(X_n)是一个随机变量，我们可以用类似的表达式来计算它的期望值，

观察我们如何用已知的f_X来替换f_g(X)，因为所有的X都遵循均匀概率分布。对于均匀概率分布，概率密度函数为：

连续均匀分布的概率密度函数

由于除区间[a, b]外，所有x的概率密度都为0，我们可以将积分改写为，

由于b-a是一个常数项，我们可以将其转换到上述表达式的左边，

用g(X_n)的期望值来表示积分I

这种形式特别有用，因为我们可以近似E(X_n)，从而直接近似积分I的值。根据大数定律，

g(X_n)的大数定律

在实际应用中，取n到∞是不可能的，所以我们认为n足够大，可以去掉极限，

代入E(X_n)的值可以得到蒙特卡洛积分。

蒙特卡罗积分

这个表达式概括了蒙特卡洛积分的思想。下面是一个Python脚本，它可以对n = 1000的积分执行近似，

一个简单的积分，它的值可以用幂法则计算，

输出为：0.32913029558796897。

这与积分的理论值很接近，

n = 10000时，输出为：0.3305301067887705。

为了理解蒙特卡洛积分的含义，这里有一个可视化图，

对于从区间[a, b]中均匀选取的每一个x值，我们计算f(x)。用(b-a)乘以f(x)得到矩形的面积，如上图所示。通过计算这些面积的平均值，我们可以得到f在区间[a, b]下曲线的近似面积。