设X是一个集合,是X的子集族(其元素称为开集),则(X,)被称为一个拓扑空间,如果下面的性质成立:
1. 空集和X是开集,
2.任意开集的并是开集,
3.有限个开集的交是开集。
这时,X中的元素称为点。我们也称是X上的一个拓扑。

以上定义中的子空间由U和Y的交集构成,现在按照上面定义中的三个要求,证明这个子空间也是拓扑空间。

以下是证明任意个集合的并还属于子空间:

以下是证明任意个集合的交还属于子空间:

以上证明可以图示如下:
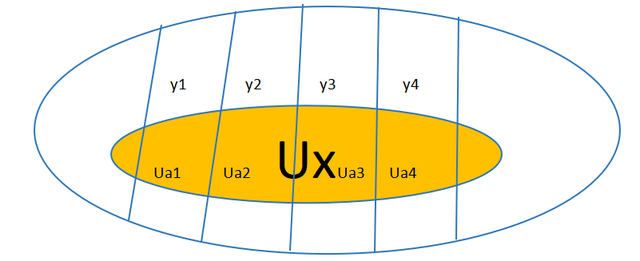
假设整个集合是X,其中的Y假设由y1,y2,y3,y4组成,Ux为彩色部分。
例如,考虑实数集R上的标准拓扑,其中开集是形如(-∞, a) ∪ (b, ∞)的集合。如果取S为R中的一个区间,例如[0,1],那么在S上定义的子空间拓扑就是所有形如[0, a) ∪ (b, 1]的集合的集合。
子空间在数学分析中有重要的应用。例如,在研究函数的空间时,我们经常考虑函数的空间中的子空间,这些子空间通常具有特殊的性质,如闭包、极限点等。此外,子空间的概念在几何和物理中也有广泛的应用,例如在研究流形上的函数时,流形上的子流形就是一个典型的子空间。

