
高斯积分几乎出现在数学和物理的所有领域,甚至在你意想不到的地方。高斯函数和𝑁维中的球体的体积有密切关系。高斯积分很强大,我希望在阅读完这篇文章后,你会同意。
高斯积分是以伟大的德国数学家卡尔·弗里德里希的名字命名的

它描述了位于𝑥=𝜇附近的钟形曲线下的面积,下方绘制的宽度对应于𝜎
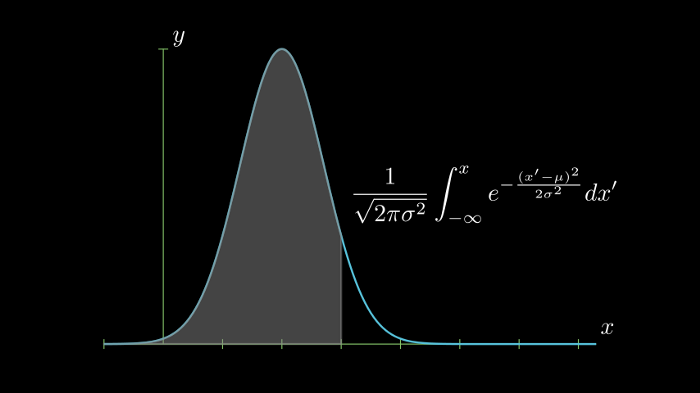
高斯积分是钟形高斯函数下的面积
我经常看到这个积分,但我总是记不住把这些常数放在哪里。前面的因数是2𝜋还是𝜋?𝜎是在平方根里面还是外面?指数是1还是1/2?
首先,让我们做一个最简单的高斯积分例子。
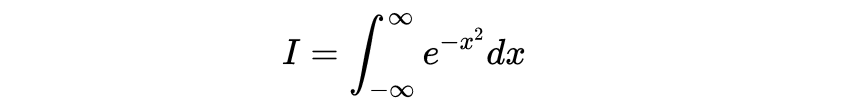
计算𝐼的诀窍是先计算𝐼²,然后取平方根。解出来后,就很容易计算
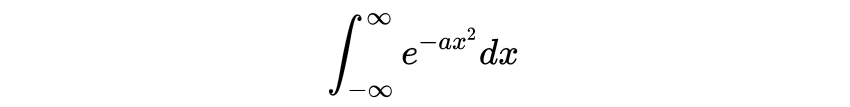
只需要做替换𝑥→𝑎𝑥,重复使用更简单的积分,

同样,我们得到
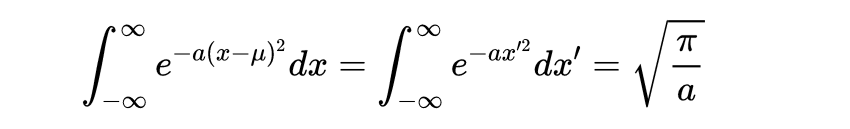
代换𝑥→𝑥−𝜇。只是稍微复杂一点的是

要做到这一点,只需计算
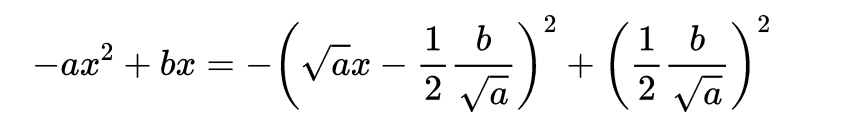
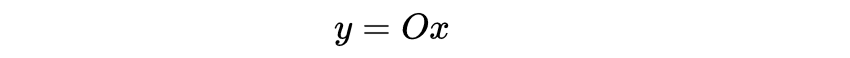
重新使用上面计算的积分:
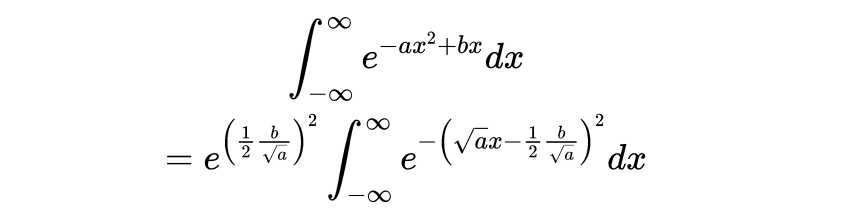

同时,我们现在知道了高斯函数的傅里叶变换。只需替换前面结果中的𝑏→𝑖𝑏。几乎不经过计算,但经过论证,就得到了广义多维版本
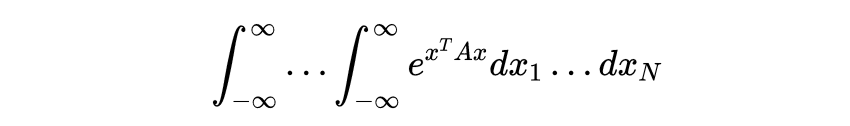
𝐴是一些(正)对称𝑁×𝑁矩阵(不一定对角线)和𝑥是列向量

论证如下。由于𝐴是一个对称矩阵,我们可以找到一个正交矩阵O,其det O=1
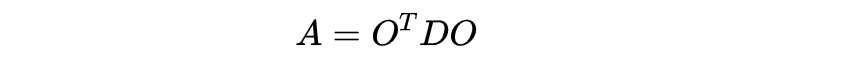
其中𝐷是一个对角矩阵。然后我们有

现在我们的替代
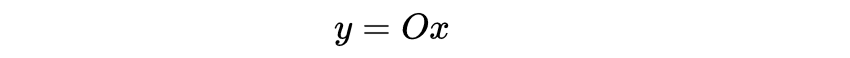
所以

𝐽是替换变换的雅可比矩阵。但是这个替换的雅可比矩阵是𝑂正交矩阵的行列式是1。由于𝐷是一个对角矩阵,我们有
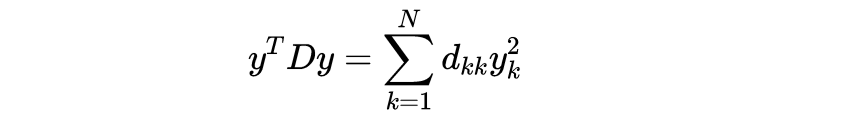
其中𝑑_𝑘𝑘是行𝑘和列𝑘𝐷的值。所以我们有

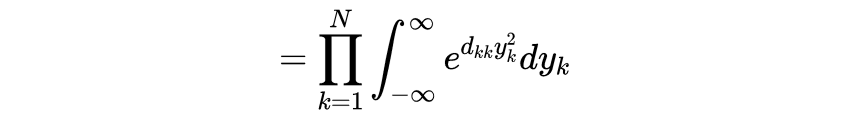

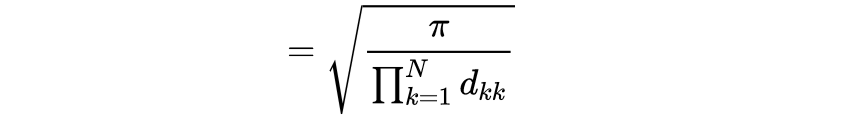

似乎我们将问题简化为从矩阵𝐴确定对角矩阵𝐷。但我们甚至不需要它。因为det𝑂=det O^T = 1
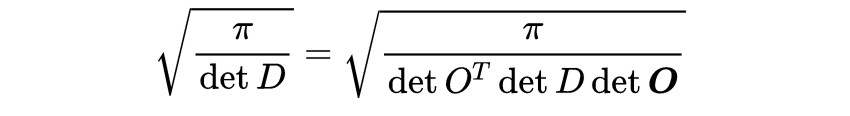

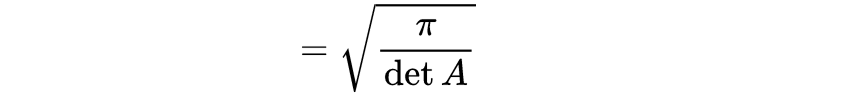
这就是广义的𝑁-维l例子的最终结果。可能有点复杂,但我认为这是一个很酷的计算。

52yx1314
文字和符号我都认识,但连在一起组成一个式子,我一脸茫然[笑着哭]
被小学生气出大病 回复 02-08 00:07
请问为什么X是对称矩阵就可以找到它的正交矩阵呢
被小学生气出大病 回复 02-08 00:08
请问极坐标系中的二重积分如何变换到平面直角坐标系中[笑着哭]
飞腾吴辉
符号很多打不出来
離傷……
一脸懵逼的看了半天只看到1 2两个数…[汗]
专家
一脸懵逼的进来,一脸懵逼的出去
我不知道这个名字到底是不是我真实的名字啊
这是严格的n维正态分布,必须要求协方差阵A是正定的;广义的n维正态是用特征函数定义的,只要求A是非负定的即可。
飞扬
就不能推荐一些初高中级别的趣味数学?
德玛西亚杯
文字部分我都认识,符号部分都认识我
寂寥山雀
有个鸡毛用?我初中还没毕业……
用户10xxx60
来呀不怕死的科学尽头是神学走起呀[笑着哭]
白开水
来啊,互相伤害啊
圣-魔
二维平面我没办法,三维物质搞得了……灌水求立方……
chenweibo39
大二的时候掌握的!真的精彩。 希望更多理工科学子懂它。
chrysanzh
居然看完了[笑着哭]
老鼠顶石头 回复 03-14 14:56
看懂了没有?不懂的话可以问我!
心的忏悔
阿拉伯数 英文字母都认得!
三言两语
应用于正态分布概率积分、统计力学等
璟岚
正态分布曲线
千里走单骑
我小学都没毕业的硬是厚着脸皮看完了!
连杰12
好文分享一下你的
霸气男爵
我的意思,每一个物 的变化 就是本身 你们用什么方式解呢 用知识解 可是这样的知识规律 你们还不明白, 你们想用知识zabcd代表你们的名字 答案 化解,对试,去做你们的答案,如你们用名字来,代表你们的名字,叫出你们的名字,写出你们的名字,一样,,你们的那些运行方式知识,你们可知道,是你们的什么运用方式 说猪得猪,说牛做牛,说马等于马,这些公式,是不是在变
{ }
他居然试图想教会我[得瑟][得瑟]
军师
虽然我不懂,但掩饰不了它的美丽[点赞]
连杰12
好文分享一下你的时候
島內
𝑁𝜎[笑着哭]
自由想象力
[点赞][点赞][点赞][点赞]还不错