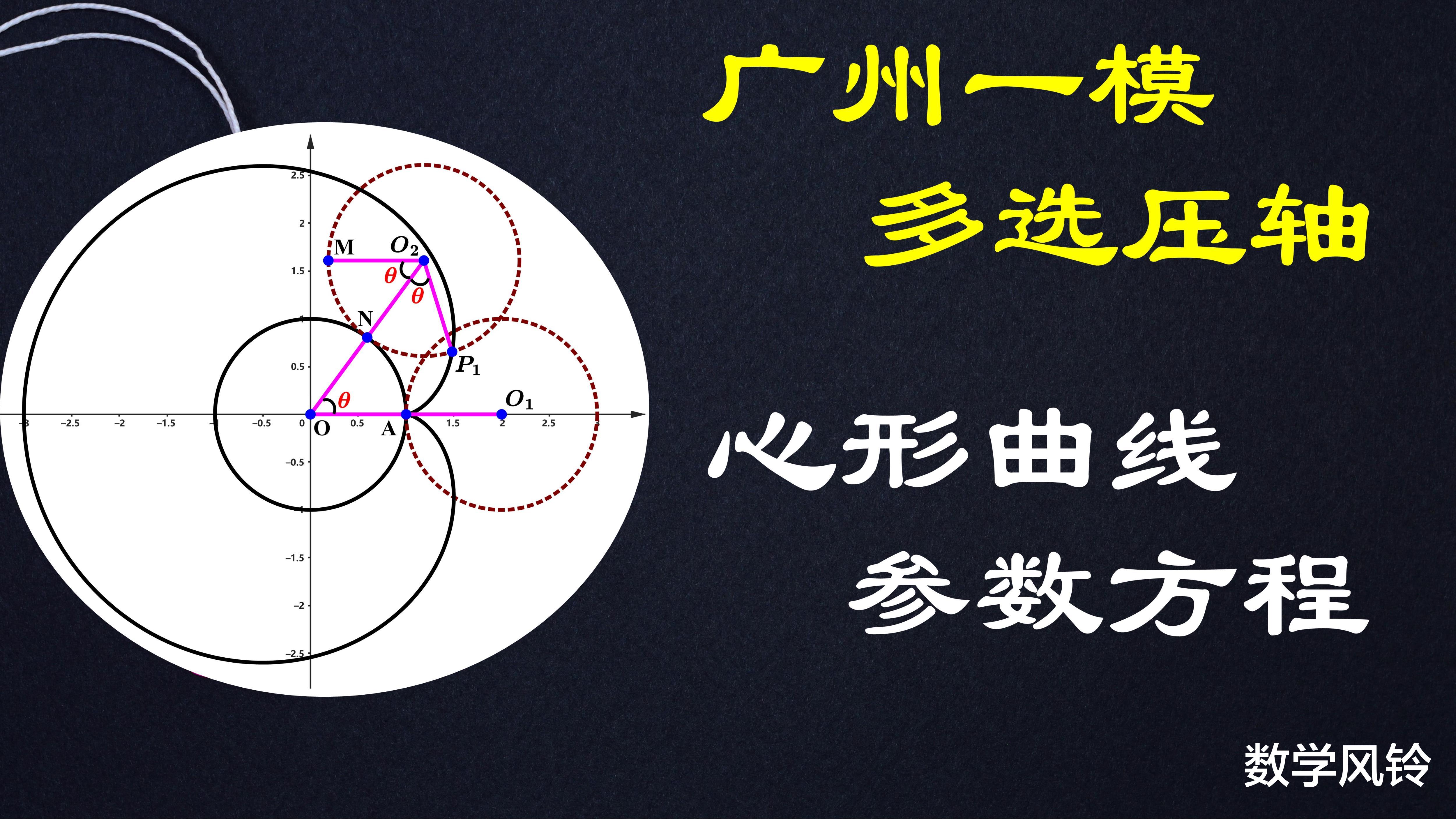
本题目出自2025届广东一模多选压轴11题,是一道新概念题型,考察解析几何新型曲线的分析,题目中给定两个全等的圆通过外侧圆滚动所形成的外旋轮线,动点的轨迹恰好构成“心形曲线”,本题目的核心需要分析心形曲线轨迹所满足的方程,由于本题目中动圆沿着单位圆外侧滚动,类似于物理中的齿轮模型,两圆相切处的“线速度”一致,动圆的圆心是绕着原点旋转的,因此在分析中可以通过旋转的角度作为参数,分析动圆圆心和动点P的坐标,同时角度信息恰好能够用于圆的参数方程。
关于圆的参数方程,实际在课本上的课后习题里面已经考察过了,人教A版选修一《圆的方程》小节中课后习题89页拓广探索第10题。

因此本题目的考点也是基于课本内容的,对于高考最后的冲刺阶段,回归课本是非常重要的。
02、心形曲线参数方程+题目求解




2025届广东一模多选压轴11题给定的心形曲线并不是我们所学过的圆锥曲线类型,分析中需要重分理解题目条件,同时要对课本上内容掌握的比较熟练,回归课本并不仅仅是过一下课本上所学的知识点,课本例题、课后习题、课后阅读材料都是高考出题的重要素材,课本上的每一个角落都不能落下。
本题所涉及到是圆的参数方程的推导思想,在最开始的部分已经做了详细介绍,参数方程的一个重要优势是在分析动点轨迹时可以独立描述横纵坐标的变化,引入的参数在题目中往往具有明确的几何意义,本题在最开始推导心形曲线的参数方程时是根据圆的参数方程结合齿轮模型,以动圆圆心转过的角度Θ作为参数进行的,圆的参数方程的论述思想是非常重要的突破点。
导出心形曲线的参数方程之后,选项A中的距离可以利用参数方程进行表示,将距离转化为Θ的函数分析很容易判断出A选项错误;选项B在A的基础上,先通过距离计算出Θ,再回代进行验证即刻判断B选项正确;选项C可以从代数和几何两个角度进行分析,几何角度更为直观,解题速度更快,代数角度则是需要构造函数,求导结合三角函数的和差化积公式分析函数的性态,判断交点个数。选项D的分析思路和C的代数角度思想是一致的,变相考察了利用导数分析三角函数的图像性质。
本题是一道难题,对基本功的考察是比较全面的,一方面是要对课本内容非常熟悉,另一方面需要有完整的知识体系,能够将解析几何和函数两大块内容综合应用。本题一定是一个非常值得研究的高质量题目,看完这篇分析一定能获益匪浅。
