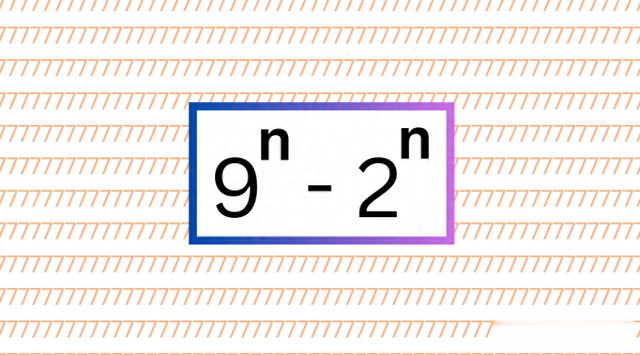
你的任务是证明对于所有正整数n , 9 ⁿ — 2 ⁿ都能被 7 整除。在处理这种类型的问题时,我喜欢尝试n的前几个值,只是为了检查这不是一个陷阱问题。也许你已经尝试过了!
嗯,9-2 = 7,但这有用吗?试试这个问题,解决方案如下,后面还有一些额外的挑战。

我们将使用一种称为数学归纳法证明的方法。首先,我们证明n = 1时的陈述,称为基准情况。然后,我们假设断言(9 ⁿ — 2 ⁿ可以被 7 整除)对于n = k且k为真。在此假设下,我们证明该断言对于n = k + 1 为真。
这就证明了,如果该断言对n的前一个值成立,那么它对n的值也成立。由于它对n = 1 成立,因此它对n = 2 也成立。由于它对n = 2 成立,因此它对n = 3也成立,依此类推,对于n的所有正整数值也是如此。
这是证明无限多个命题的聪明方法。你可以把它想象成推倒一连串的多米诺骨牌。
让我们从基本情况开始。如果n = 1,那么
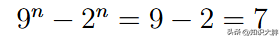
可以被 7 整除。☑️
基本情况完成后,假设断言对n = k成立。也就是说,我们假设 9ᵏ — 2ᵏ可以被 7 整除。我们称之为归纳假设。现在我们需要证明

可以被 7 整除。我们首先使用幂规则以稍微不同的方式写出它。

我们需要重新排列右侧,以便出现9 ᵏ — 2 ᵏ 。如果右侧2 ᵏ乘以 -9,我们可以分解出 9。让我们实现它。

现在将 9 分解出来。
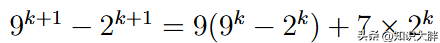
右边有两个重要项。7 * 2 ᵏ是 7 的倍数,所以可以被 7 整除。根据归纳假设,9(9 ᵏ — 2 ᵏ ) 可以被 7 整除。这意味着整个右边以及左边都可以被 7 整除,正如要求的那样。
我们有足够的理由通过数学归纳法得出 9 ⁿ — 2 ⁿ可以被 7 整除的结论。✅
归纳证明是数学世界中一项重要的技巧。它用于证明各种重要结果,例如算术基本定理、二项式定理和 Jordan-Hölder 定理。
挑战 1:证明对于所有正整数n ,前n 个完全平方数的和1² + 2² + … + n ² = n ( n + 1 )(2 n + 1 )/6 。
挑战 2:证明对于所有正整数n , 3^(2 n + 4) — 2^(2 n ) 都能被 5 整除。
挑战 3:“强归纳法”要求假设你的论断对每个小于n的正整数都成立。利用这一点来证明算术基本定理的第一部分,即证明每个正整数都可以表示为素数的乘积。
