
如上图所示,中考几何计算题,求霸王枪CD的长度。
本题来自抖音作者,解法很多,先给出抖音评论区里没有的解法,最后展示评论区的解题高手提供的精彩答案。
审题:本题出现了乾坤圈⊙O,就是说四边形ABCD四点共圆,是圆内接四边形。又知道∠ADC=45°,再加上AB是直径,就是暗示三角形ABC是等腰直角三角形。
为什么呢?因为直径所对的圆周角是直角,同弦或等弦所对的圆周角相等(希腊七贤之首的泰勒斯首先发现并表述),所以∠ADC=∠ABC=45°,所以三角形ABC是等腰直角三角形。根据已知条件,霸王枪CD是直角∠ADB的角平分线。圆内接四边形的两条对角线又是相交弦。所以题目暗示我们可以用相交弦定理或托勒密定理解题。
解法一:(相交弦定理)设圆中弦CD与直径AB交于点E,故AE·BE=CE·DE。我们先求AE。因为CD是角平分线,故交点D分对边成两段与直角ADB的两边成比例。即

现在求角平分线DE。可以用下图所示的库斯顿定理。

计算过程请看下图:

∵AE·BE=CE·DE(相交弦定理),现在可以求出CE。计算过程如下:

现在可以得到CD的长度了:
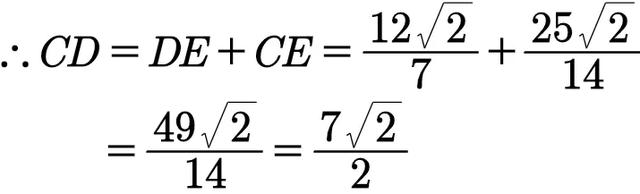
答案
解法二(坐标法)
建系,设A(0,0), B(5,0),先求点D的坐标。点D的纵坐标易求。设它为y,可得y=3×4÷5=2.4。再求横坐标x。用勾股定理可得x²=9-5.76=3.24,所以x=1.8,即D(1.8,2.4)。再求点C的坐标。因为△ABC是等腰直角三角形,所以有C(2.5,-2.5)。已知两点坐标,可以用公式求两点之间的距离。

解法三(余弦定理)勾三股四弦五这句话最早出自古代数学家商高,所以我们可以把△ABD称为商高三角形。

在三角形ABD中应用余弦定理求角A,得
cosA=(b²+c²-a²)/2bc=18/30=3/5=0.6
arccos0.6=cos⁻¹(0.6)=0.927295(弧度)=53.13°
width | cos(0.927295) = 0.6
height | sin(0.927295) = 0.8

因为∠CAB=45°,所以
∠DAC=53.13°+45°=98.13°
cos98.13°=-0.14141958...
≈-0.1414196
现在求AC。因为三角形ACB是等腰直角三角形,我们考虑正方形的边长和对角线之间的函数关系。设正方形的边长为x,对角线为y,应用勾股定理得
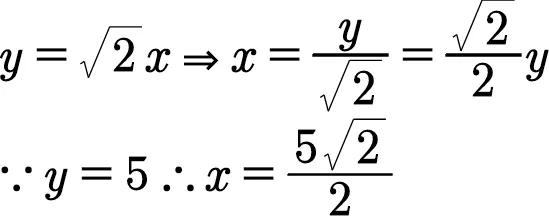
AC=BC=x
求出AC后,在三角形ACD中,已知两边和夹角,应用余弦定理可立即求出CD的数值解。

解法四(相似法)相交弦定理告诉我们交点分线段成比例,所以我们可以利用相似三角形对应线段成比例分别计算CE和DE,再求和即可求得CD。

∵同弦所对圆周角相等,所以三角形ACE∽三角形DBE,∴对应线段成比例。

解法五(正弦定理)在三角形ADC中应用正弦定理,可以立即求得CD。请看下图:
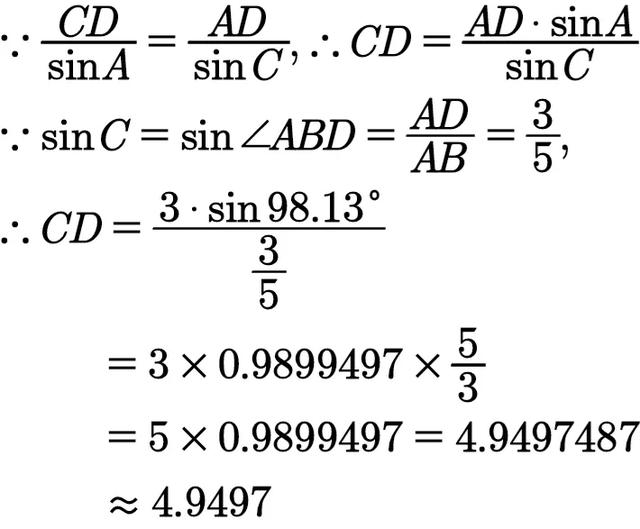
因为同弦所对圆周角相等,所以可以求得sinC。(sinC=sin∠ACD=sin∠ABD)
本题圆的直径来的轻松。此外,还有一个求直径的公式。
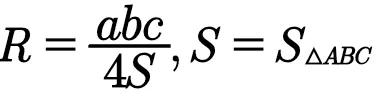
还可以这样计算:

答案的精度可以参看下图

正弦定理的知识概括

正弦定理可以这样推导(用三角形面积公式推导)

正弦定理和余弦定理简史
正弦定理和余弦定理是讨论任意三角形边角关系的重要工具,它们的发现是三角学发展史上的重要里程碑。
公元150年左右,古希腊数学家托勒密实质上已经知道了正弦定理,它的第一个证明是波斯历史学家阿尔·比鲁尼(973~1048)给出的。阿拉伯天文学家那西尔·艾丁在1250年左右也给出了正弦定理。
余弦定理实际上是欧几里得(前330~前275)所著《几何原本》第二卷的命题12和13。公元6世纪,印度的阿尔亚霍得(约476~550)在历书中给出了余弦定理。
接下来介绍评论区的答案。
评论区答案集锦和评注解法一(托勒密定理)
若四边形内接于圆,则它的两双对边的乘积之和等于两对角线的乘积。
计算过程如下

托勒密定理(Ptolemy theorem)简介
托勒密(约100~约170)是古希腊天文学家,他继承前贤,特别是希帕克斯和梅内劳斯的成就,并加以整理和发挥,著作《天文学大成》被阿拉伯人译作《至大论》。该书共13篇,其第一篇主要讲球面三角,在讨论如何计算弧所对弦的长度时,托勒密把这个定理作为一个引理提出。书中,托勒密利用这个定理导出了包括加法公式在内的一系列重要的三角公式。
解法二(手拉手模型)作为中考数学的解题大招,这个模型有很多结论。下图所示为冰山一角。

推荐观看视频链接
抖音链接(手拉手模型全部结论)朱韬讲数学https://www.douyin.com/video/7427699206971854134/?region=CN&mid=7427700095769938698&u_code=0&titleType=title&share_sign=VEQnBagu85j1kNaR_1YpljPTeVOAIyysWlEmaeIRJzY-&share_version=7010040&ts=1736675188&from_aid=482431&from_ssr=1
解法请看下图
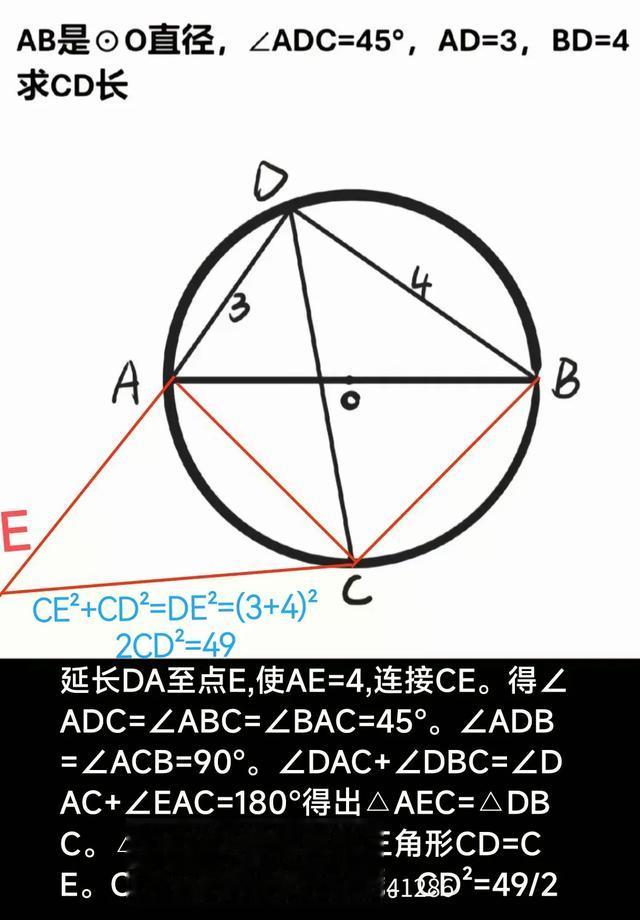
评论区高手云集,解法很漂亮,辅助图形构思巧妙。图中有全等三角形,也有相似三角形,请读者细细品味。
解法三(勾股定理)请看下图,一目了然。

科学尚未普及,媒体还需努力。感谢阅读,再见。

周末到了,可以放松一下,放飞自我,oh
yeah.祝大家周末愉快。
