
上图中的符号

其中h的含义为



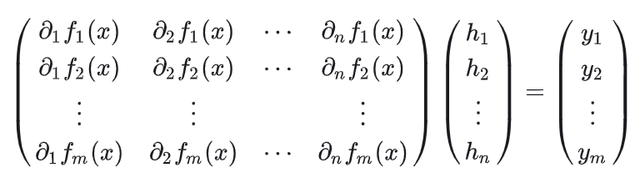

这个定理的意思大概是,当把Fréchet微分的定义从一维推广到n维赋范线性空间的时候,其相应产生的n维无穷小量的向量h=(h1,h2,h3,......),对于原函数f的导数来说,其运算也符合全导数的线性运算规则:
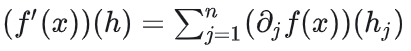


上图中的符号

其中h的含义为



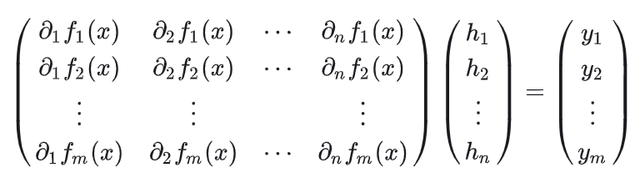

这个定理的意思大概是,当把Fréchet微分的定义从一维推广到n维赋范线性空间的时候,其相应产生的n维无穷小量的向量h=(h1,h2,h3,......),对于原函数f的导数来说,其运算也符合全导数的线性运算规则:
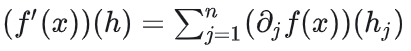

作者最新文章
教育TOP
教育最新文章
热门分类