逆算子定理是指,在巴拿赫空间中,如果一个有界线性算子是双射(即既是单射也是满射),那么它的逆算子也是有界线性算子。换句话说,如果一个有界线性算子是双射,它不仅能够一对一地映射输入到输出,还能保持映射后的结果具有有界性,这意味着逆算子本身也是一个有界线性算子。


这里的可逆性指的是存在连续线性逆。根据逆算子定理,我们只需要证明 S 是双射。任取

图1
注意这里范数
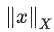
与

相等,是因为T(x)是空间Y的元素,T-1是作用于Y上的元素。
图1中的证明还用到了三角不等式,以及x的范数等于-x的范数。
范数的齐次性是范数的一个重要性质,它表明对于任意标量α和向量x,有‖αx‖=|α|‖x‖1。当α取-1时,该性质即表明向量x的范数等于其相反向量-x的范数,即‖-x‖=|-1|‖x‖=‖x‖1。
因此,可以得出结论:x的范数等于-x的范数。

