
Deepseek的创始人梁文锋写道:“每当工作中遇到困难,我就会想起西蒙斯的话:‘一定存在为价格建模的方法。’”
part 1 分析钻石的价格微分比积分更难形象化。面积,体积,这些都是易于感知和理解的,与此相反,因为微分是“比值”,所以在理解上并不是很容易。
“比值”这种“除法世界”的东西虽然不易于理解,但是在“捕捉变化”时,却是非常有用的“神兵利器”。
积分和微分的思考方法完全不一样。下面我们结合实际的例子,来转换大脑的思路。最开始的题目是钻石的价格公式。
Q:为什么选择钻石的价格公式?
A:像微分这种很抽象的话题,用具体的金钱问题来思考是一种技巧。比如小学生的题目中,在数字后面加上“日元”,算术问题就容易理解。对于成年人来说,用钞票比用经济增长率或者汇率更能让人感受到其数量。这是同一种原理。
我们想象金钱时,对数量的感觉会变得敏锐,那么我们就利用这种“量的感觉”来举例吧。
根据美国宝石研究院的《钻石质量评价国际标准》,钻石的价值由4C决定。4C指的是钻石的特征,即克拉重量(Carat Weight)、色泽(Color)、切工(Cut)、净度(Clarity)。除了4C,还存在其它投机因素也能使钻石价格发生变动,但多方面考虑会使问题变得过于复杂,所以忽略不计了。
制定钻石价格的一般公式有些难,在此我们假设钻石的色泽、切工、净度都相同。这样一来,钻石的价格就由“大小”(重量)决定。钻石重量的单位是克拉,1克拉相当于0.2克。

当克拉重量不太大时,钻石的价格与“克拉重量的平方”成比例。也就是说,如果钻石的重量(克拉)为x,那么钻石价格y可以表示成
y=x²·1克拉的价格
这个关系式称为“平方法”。
实际上1克拉的钻石价格并不是固定的,但为了方便解释,我们假设“1克拉钻石价格为100万日元”。这样一来,x克拉的钻石价格为
y=100x²万日元
如果重量是2克拉,那么钻石价格为
100×2²=400万日元
实际上,钻石恰好是1克拉的情况并不常见。多数情况下是0.98克拉、1.01克拉等等。因此,假设钻石重量不是1克拉,而是1.1克拉,这时钻石价格是100×1.1²=121万日元。重量仅增加0.1克拉,价格就增加了21万日元。
0.1克拉是0.02克,仅仅增加这样一点点重量,价格竟增加了21万日元(约人民币12000元)。碳元素也变得让人另眼相看了。(另外,也存在克拉重量增大,但不能套用此平方法的情况,详情参阅注释)
在这里,假设钻石的重量在x克拉的基础上增加了Δx,即为x+Δx克拉。克拉重量减少也是同理,不过为了方便计算,在此只讨论增加的情况。
Q:此时,你觉得钻石价格如何增加?
A:是不是像刚才计算的那样,仅仅增加一点点重量,价格就增加好多?

如图58所示,边长为x的正方形,当横边与纵边分别增加Δx时,面积会增加多少呢?通过这张图,我们就能明白钻石重量在x克拉的基础上增加了Δx,即为x+Δx克拉时,价格上涨了多少。
在这里,x²(乘以100万日元)表示的是钻石价格。价格上涨的部分如图58所示,是“两个长方形(面积均为xΔx)加上边长为Δx的正方形(面积为(Δx)²)”。
也就是说,钻石价格增加部分是
(2xΔx+(Δx)²)×100万日元
在刚才的例子中,当1克拉的钻石增加为1.1克拉时,其价格增加的部分表示为
(2×1×0.1+(0.1)²)×100万日元
=20万日元+1万日元
(Δx)²的部分是1万日元,单纯看会让人觉得这部分增长与重量增加相符,但是与20万日元相比,这个金额就相对较小了。
如果把Δx变得更小,这种倾向会更加明显。比如
Δx=0.05.(2×1×0.05+(0.05)²)×100万日元
=10万日元+2500日元
(Δx)²变成了1万日元的¼,即2500日元。再比如Δx=0.02.
(2×1×0.02+(0.02)²)×100万日元
=4万日元+400日元
(Δx)²变成了400日元。
一般而言,“小正方形的部分”比“长方形的部分”便宜。
过于小的(Δx)²,被扔进垃圾桶(图59)。

另外,虽然说(Δx)²是Δx的Δx倍,但是这并不代表数量也增加了。小于1的数相乘,结果会变得更小。(Δx)²和Δx相比的话,相对来说数值更小。
忽略(Δx)²后,钻石价格增加的部分大致为
2xΔx×100万日元
Q:2xΔx×100万日元?这到底表示什么意思?
A:用图59来说的话,指的是两个长方形的面积。即和Δx相比,无法被忽略的部分。
重要的一点是,和Δx相比,是大还是小。比如
2xΔx×100万日元
这个数值虽然随着Δx的变小而变小,但是并不能说这个数值“和Δx相比较小”。
关键是和Δx相比,无法被忽略的部分
2xΔx×100万日元
是Δx的多少倍呢?答案是2x×100(万日元)=200x倍。y=100x²的微分指的就是这个倍数200x。
钻石的例子从一开始设定的就是1克拉=100万日元,所以价格增加的部分是“1克拉的2x倍”。这个“2”用图59来表示的话,就是来自于像两堵墙壁一样的部分。

丢弃可以忽略的部分,只留下不能忽略的部分,再求出“不能忽略的部分是Δx的多少倍”,这就是微分。

微分的要领:
准确区分可以忽略的部分与不能忽略的部分。
忽略较小部分,取近似值。
part 2 幂函数的微分公式下面的公式,大家是否有似曾相识的感觉?
(xⁿ)'=nxⁿ⁻¹ (n=1,2,3,...)
这就是高中微积分最先学习的幂函数的微分公式。
高中老师会教大家幂函数的求导法则:总之,求导时要把指数的数值写在前面,然后把右上角的数值减1。但是为什么要这样做呢?在数学中,“总之要这样做”这种强加于人的规则确实存在,不过我们在此稍作停顿,来思考其中的本质。
实际上,幂函数的微分公式可以用我们处理钻石问题的要领来思考。
也就是说,我们可以把它变成这样一个问题:存在一块边长为x的正方形土地,其面积为x²,如果把土地边长分别增加Δx,那么土地的面积会增加多少?

求函数y=x³的导数。
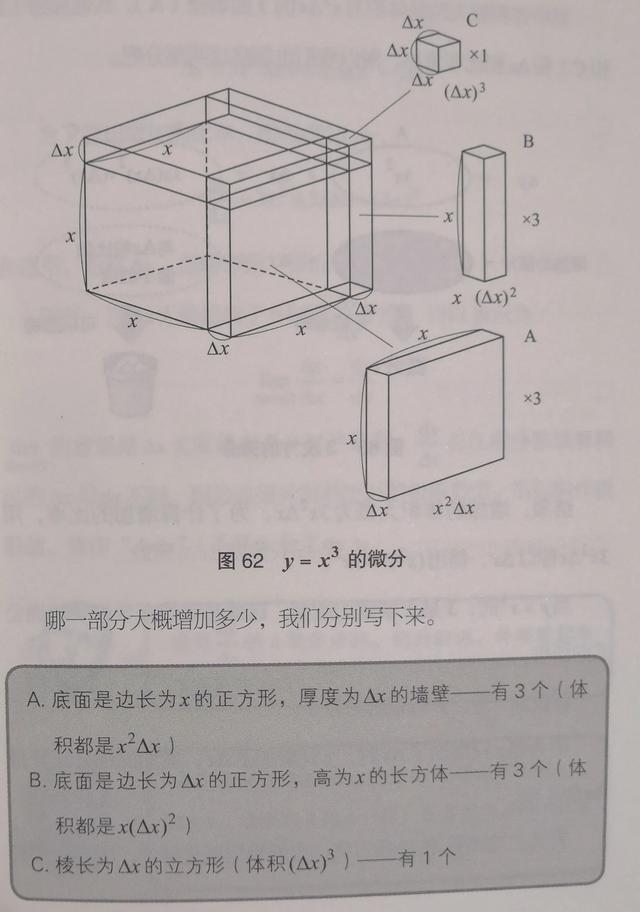

(xⁿ)'=nxⁿ⁻¹ (n=1,2,3,...)
公式的证明见下图。

上面的公式其实可以推广到n为任何实数,普通的证明思路是用对数求导法。不过,学校教过函数的和差积商的导数。这里重点说一下积的导数。
两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个函数乘以第二个函数的导数。即
(fg)'=f'g+fg'.
谈到两个函数f(x)和g(x)的乘积的微分很抽象,我们用老办法,把它转化为面积问题来思考就容易理解了。
请看下图。

乘积的微分公式是17世纪由牛顿提出来的,这是一个非常大的进步。
我们用上面的法则来验证幂函数的微分公式可以推广到n为任何实数。
举个例子,设n=½。
x的½次方=√x,x=(√x)²。
应用乘积的微分公式,会得到下面的结果。我们从x的微分等于1开始。
1=x'
=(√x·√x)'
=(√x)'·√x+√x·(√x)'
=2√x·(√x)'
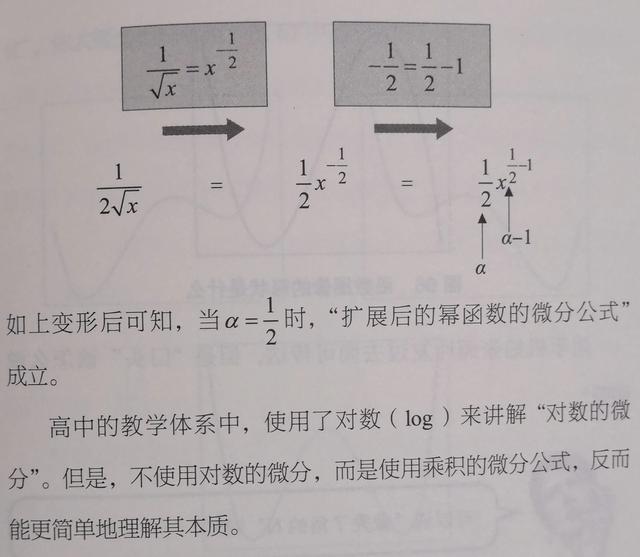
两边除以2√x得到

由以上可知,当α=½时,公式
(xᵃ)'=αxᵃ⁻¹成立。
钻石价格的注释见下图。


幂函数的微分公式推广后如何证明?作者提供的证明思路如下图所示。即原著的注释9.

书摘信息见下图。

科学尚未普及,媒体还需努力。感谢阅读,再见。
祝大家春节快乐,巳巳如意。[福][礼物][发][爆竹][烟花][红包]



