
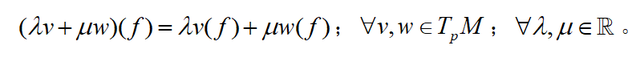
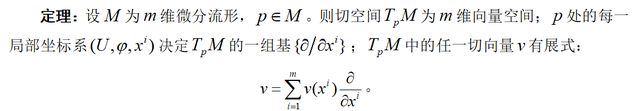
证明:

这是按照定义中的第三条leibniz法则得到的结论。
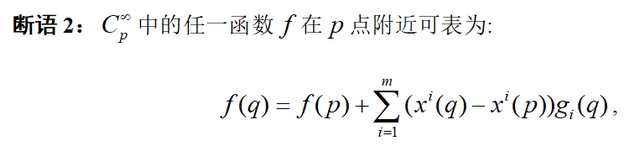
图1
这是按泰勒级数展开,参考
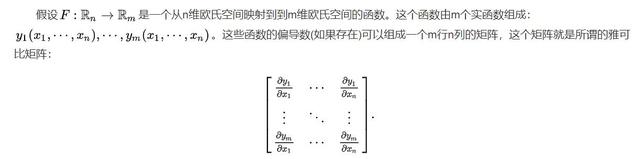

图1中:
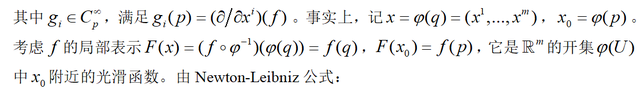
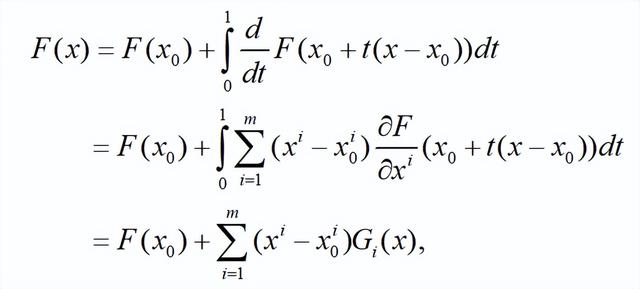
图中的积分号其实就是函数F本身。关于x0+t(x-x0),可以参考作者《流形的切空间》一文。因为F是f的局部表示,上图的第二个等号应用了图1的展开式,第二个等式的积分号中好像少了一个微分号d/dt。
其中
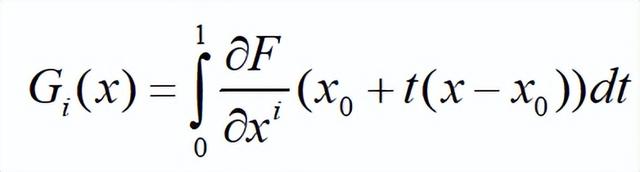
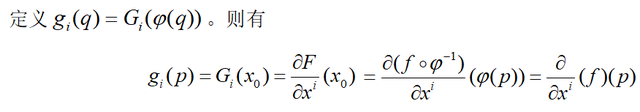

对比
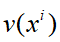
与
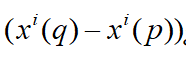
两者的意义,表示的都是通过p点的切向量在坐标轴xi下的坐标(q变化,p固定)。

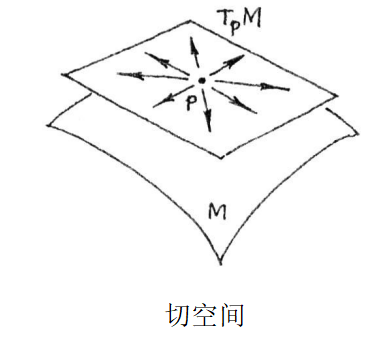
整个定理的意思就是,切空间的任一向量v都可以以偏导数为坐标轴进行展开。


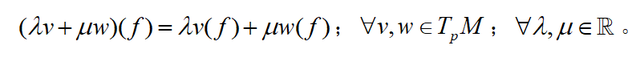

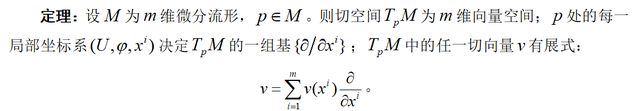
证明:

这是按照定义中的第三条leibniz法则得到的结论。
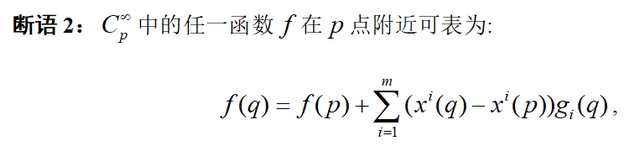
图1
这是按泰勒级数展开,参考


图1中:
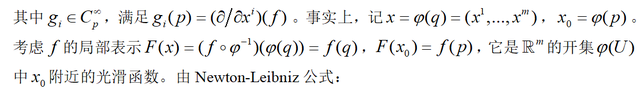
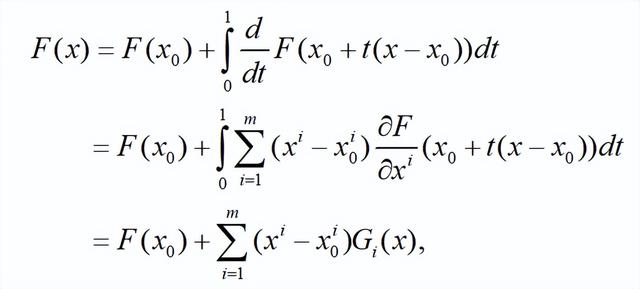
图中的积分号其实就是函数F本身。关于x0+t(x-x0),可以参考作者《流形的切空间》一文。因为F是f的局部表示,上图的第二个等号应用了图1的展开式,第二个等式的积分号中好像少了一个微分号d/dt。
其中
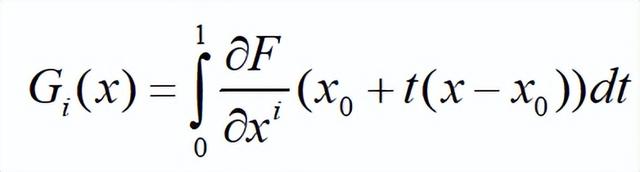
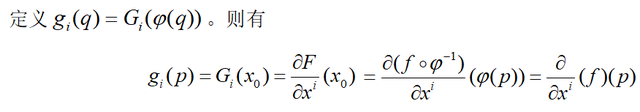

对比
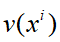
与
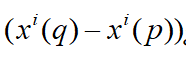
两者的意义,表示的都是通过p点的切向量在坐标轴xi下的坐标(q变化,p固定)。

整个定理的意思就是,切空间的任一向量v都可以以偏导数为坐标轴进行展开。

作者最新文章
教育TOP
教育最新文章
热门分类